红黑树

　　对于红黑树，网上的资料有许多许多，有好多大牛都对其进行了研究，但是在此我任然想写篇博客，我认为看别人的东西，我们只能够理解，但如果能够写出来，就能更进一步深入，废话我就不多说了，下面就直接介绍吧。

　　红黑树是一种二叉查找树，但每个节点上又增加了一个储存为表示节点的颜色，可以是红色或者黑色。通过对人和一条从根到叶子的路径上各个着色方式的限制，红黑树确保每一条路径都不会超过最短路径的两倍，因而是接近平衡的。一颗高度为h的二叉查找树可以进行任何一种基本的动态集合操作。如：查找、删除、排序等等。当二叉查找树的高度较低时，这些操作执行的比较快，但当二叉查找树的高度较高时，这些操作的性能可能不比用链表好。红黑树是一种平衡的二叉查找树，它能保证在最坏的情况下，基本的动态操作集合时间为O（lgn）。正因为它在实践中效率较好，所以得到了广泛引用。如：关联数组，在c++STL中也用到许多（如：set, multiset, map, multimap等）。

　　1、红黑树的性质

　　红黑树的每个节点包括五个域：color、key、left、right和parent。如果节点没有一个字节点，则该节点被称为叶子节点。在有些书中，将该节点的父节点相应的指针parent域的值为NIL（并不是为NULL指针）。把NIL视为指向红黑树外界点的指针，把带有关键字的节点视为内节点。红黑树节点的结构定义如下：

/*定义结点的颜色*/
 typedef enum Color
 {
        RED   = 1,
        BLACK = 0
 }Color;
typedef struct Node
{
    struct Node *parent;  //父节点
    struct Node *left;    //左子树
    struct Node *right;   //右子树
    int          key;     //数据域
    Color        color;   //节点颜色
}Node,*RBTree;

　　性质如下：（1）每个节点为红色或者黑色。

　　　　　　　（2）根节点必须为黑色。

　　　　　　　（3）每个叶子节点为黑色。

　　　　　　　（4）如果一个节点为红色，则它的两个儿子都为黑色。

　　　　　　　（5）对于每条路径上的黑节点数目要相等。

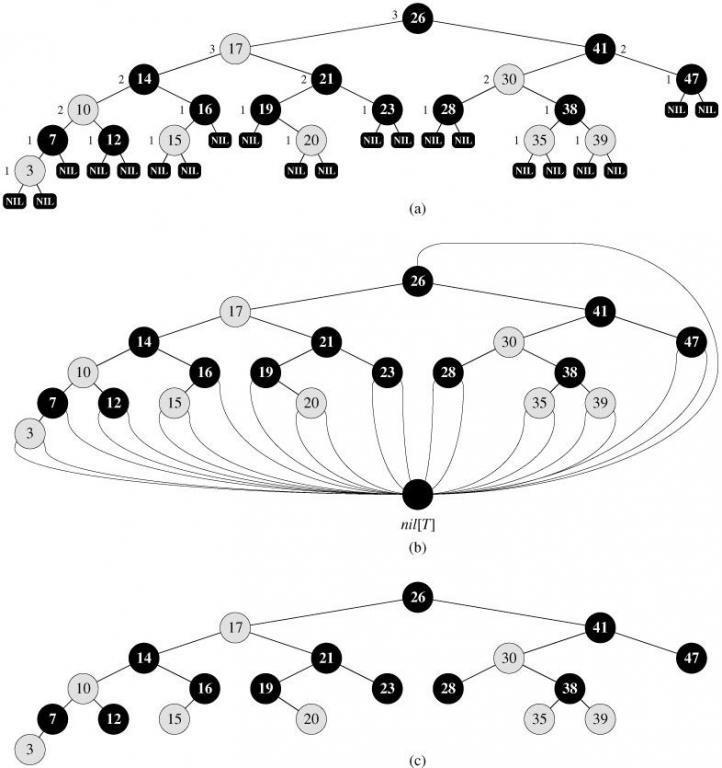
从图(a)可以看出NIL不是空指针，而是叶子节点。《算法导论》中将其视为哨兵，这样可以方便对红黑树进行相关操作，当然也可以将其省略，即图(c)。

在此有个引理证明了红黑树是一个很好的查找树：定理：一棵拥有n个内部结点的红黑树的树高之多为2log(n+1) 。证明：首先定义一颗红黑树的黑高度Bh为：从这颗红黑树的根结点（但不包括这个根结点）到叶结点的路径上包含的黑色结点（注意，包括叶结点）数量。另外规定叶结点的黑高度为0。 
下面我们首先证明一颗有n个内部结点的红黑树满足n>=2^Bh-1。这可以用数学归纳法证明，施归纳于树高h。当h=0时，这相当于是一个叶结点，黑高度Bh为0，而内部结点数量n为0，此时0>=2^0-1成立。假设树高h<=t时，n>=2^Bh-1成立，我们记一颗树高为t+1的红黑树的根结点的左子树的内部结点数量为nl，右子树的内部结点数量为nr，记这两颗子树的黑高度为Bh'（注意这两颗子树的黑高度必然一样），显然这两颗子树的树高<=t，于是有nl>=2^Bh'-1以及nr>=2^Bh'-1，将这两个不等式相加有nl+nr>=2^(Bh'+1)-2，将该不等式左右加1，得到n>=2^(Bh'+1)-1，很显然Bh'+1>=Bh，于是前面的不等式可以变为n>=2^Bh-1，这样就证明了一颗有n个内部结点的红黑树满足n>=2^Bh-1。 
下面我们完成剩余部分的证明，记红黑树树高为h。我们先证明Bh>=h/2。在任何一条从根结点到叶结点的路径上（不包括根结点，但包括叶结点），假设其结点数量为m，注意其包含的黑色结点数量即为Bh。当m为偶数时，根据性质5可以看出每一对儿相邻的结点至多有一个红色结点，所以有Bh>=m/2；而当m为奇数时，这条路径上除去叶结点后有偶数个结点，于是这些结点中的黑色结点数B'满足B'>=(m-1)/2，将该不等式前后加1得出Bh>=(m+1)/2，可以进一步得出Bh>m/2，综合m为偶数的情况可以得出Bh>=m/2，而m在最大的情况下等于树高h，因此可以证明Bh>=h/2。将Bh>=h/2代入n>=2^Bh-1，最终得到h<=2log(n+1)。证明完毕。

　　2、旋转操作

　　在红黑树上进行差入或者删除操作时，会改变树的结构形态，结果导致可能不满足红黑树的性质，为了保证每次进行操作后，任然保持红黑树的特性，需要改变树中有些节点的颜色和指针结构。其中指针的结果通过旋转操作来完成，旋转有两种：左旋转和右旋转。

 

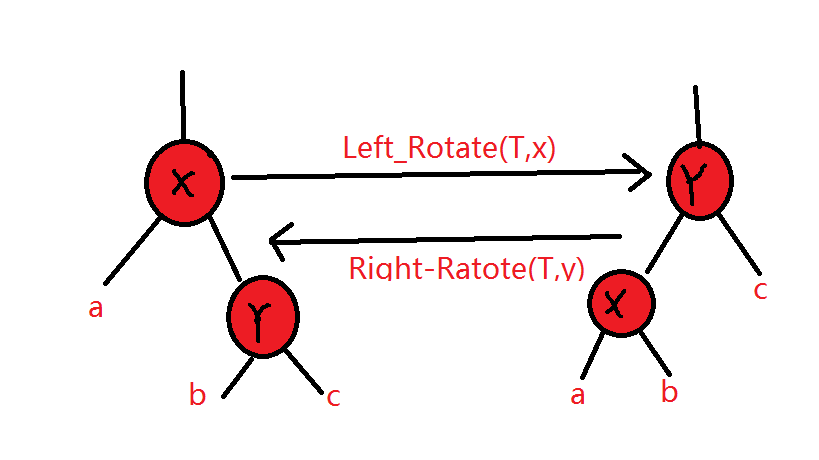
　　从图中左右旋转过程可以看出，对x节点进行左旋转，则旋转过程：x的右孩子设置为y的左孩子b，y的父节点设置为x的父节点，y的左孩子设置为x。对y做右旋转过程为：将x的右孩子b设置为y的右孩子，将y设置为x的右孩子,x的父节点设置为y的父节点即可。下面给出相应的伪代码：

LEFT_ROTATE(T,x)
    y=right[x]//获取右孩子
    right[x]=left[y]//设置x的右孩子为y的左孩子
    if left[y]!=NULL
        then parent[left[y]]=x
    parent[y]=parent[x];
    if parnet[x]==NIL
        then root[T]=y
        else if x==left[parent[x]]
            then left[parent[x]]=y
            else right[parent[x]]=y
    left[y]=x;//设置y的左孩子为x
    parent[x]=y//设置x的父节点为y

RIGHT_ROTATE(T,y)
    x=left[y]//获取左孩子
    left[y]=right[x]//设置y的左孩子为x的右孩子
    if right[x]!=NULL
        then parent[right[x]]=y
    parent[x]=parent[y];//设置x的父节点为y的父节点
    if parnet[y]==NIL
        then root[T]=x
        else if y==left[parent[y]]
            then left[parent[y]]=x
            else right[parent[y]]=x
    right[x]=y;//设置x的右孩子为y
    parent[y]=x//设置y的父节点为x

 　　3、插入

　　红黑树插入一个节点过程：先按二叉排序树的插入过程将节点插入红黑树中，然后将节点标记为红色（原因：与红黑树的性质3可知，插入之前所有根至外部节点的路径上黑色节点数目都相同，所以如果插入的节点是黑色肯定错误（黑色节点数目不相同），而相对的插入红节点可能会也可能不会违反“没有连续两个节点是红色”这一条件，所以插入的节点为红色，如果违反条件再调整即可），在调整节点或重新着色。

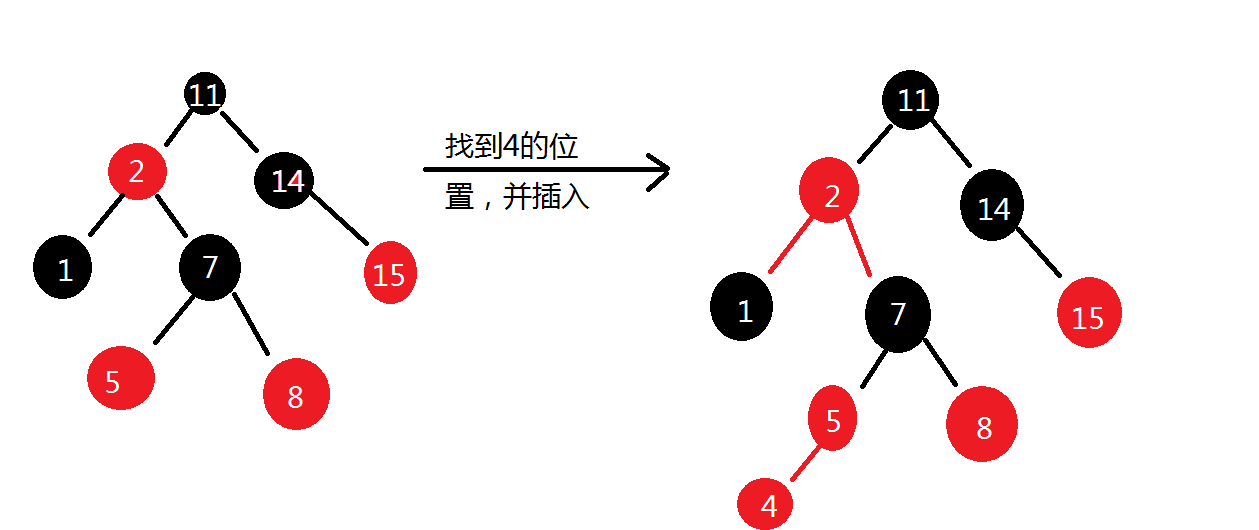
　　说先我们来分析向红黑树中插入节点和破坏那些性质，因为每次插入一个节点总是标记为红色，这样性质2和性质4可能被破坏。并且每次插入一个的节点，如果破坏了红黑树的性质，则至多只能破坏其中的一条性质，并且不是性质2就是性质4。如果性质2被违反了，则红色的根节点必定是新增加的节点，违反性质2在整个插入过程中只有一次。所以违反性质2的节点直接将其节点的颜色改为黑色即可。

　　剩下的问题都是处理违反性质4的，这种有3种情况：

　　　　情况1，z的叔叔y是红色的。
　　　　情况2：z的叔叔y是黑色的，且z是右孩子
　　　　情况3：z的叔叔y是黑色的，且z是左孩子

对于情况1：

对于情况2和情况3：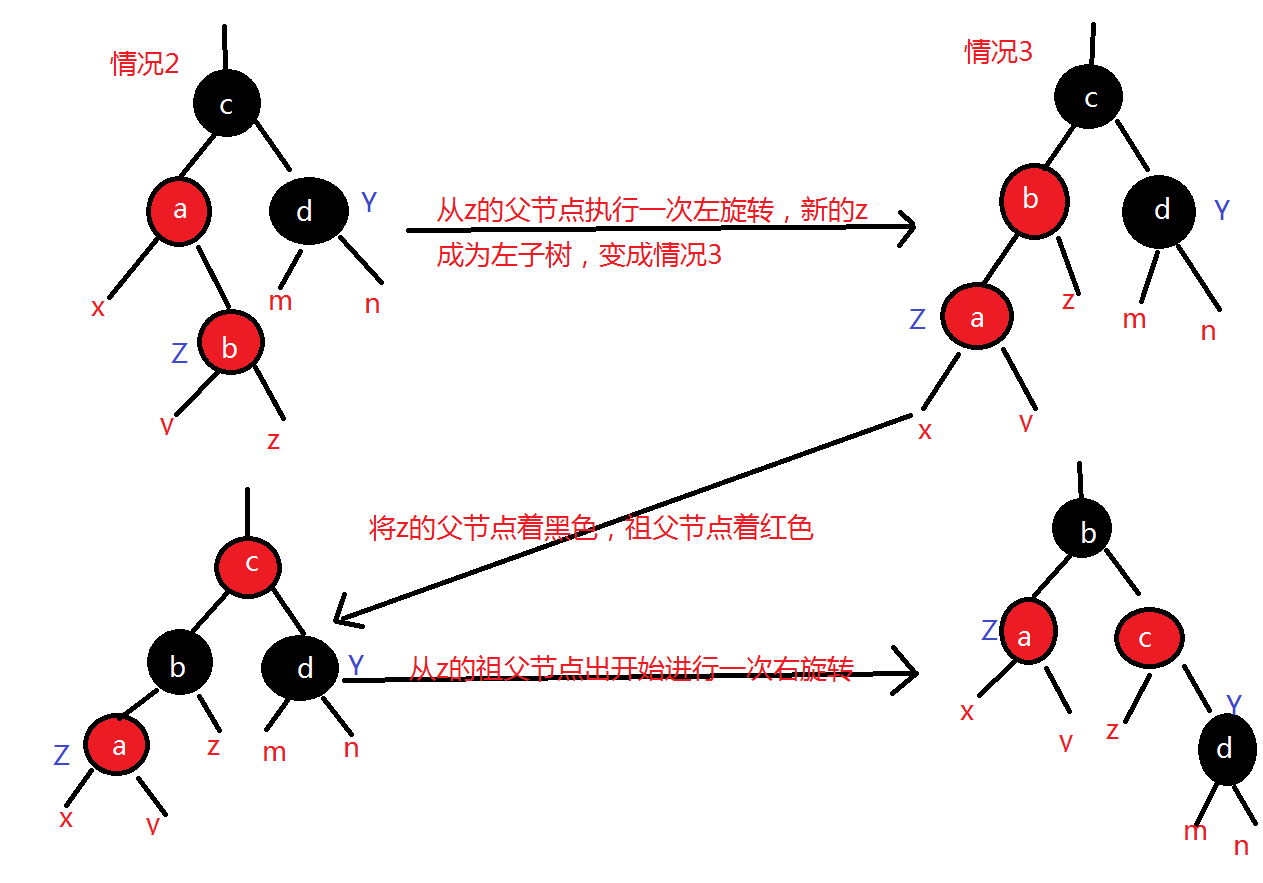

茶如伪代码：

RB_INSERT(T z)
    y=NIL//将y设置为哨兵，将x设置为根
    x=root[T]
    while x!=NIL//实现搜索，如果z比x小，向左子树搜索，否则向右子树搜索，并在适当的位置插入y
        do y=x
            if key[z]<key[x]
                then x=left[x]
            else x=right[x]
    parent[z]=y
    if y=NIL
        then root=z
    else if key[z]<key[y]
        then left[y]=z
    else right[y]=z
    left[z]=NIL
    right[z]=NIL
    color[z]=RED//将插入的节点标记为红色
    RE_INSERT_FIXEDUP(T z)//进行调整，使之满足红黑树的性质

 调整的伪代码：

RE_INSERT_FIXEDUP(T z)
    while color[parent[z]]=RED
        do if parent[z]==left[parent[parent[z]]]
            then y=right[parent[parnet[z]]]
                if color[y]==RED//情况1，z的叔叔节点为红色
                    then color[parent[z]]=BLACK
                    color[y]=BLACK
                    color[parent[z]]=RED
                    z=parent[parent[z]]
                else if z==right[parent[z]]//情况2
                    then z=parent[z]
                    LEFT_ROTATE(T z)
                    color[parent[z]]=BLACK//情况3
                    color[parent[parent[z]]]=RED
        else (same as then clause with "right" and "left"exchanged)
    color(root[T])=BLACK//将根节点设置为黑色

　　4、删除

　　红黑树的删除功能最为复杂，与二叉查找树类似，删除节点有3中情况：（1）无左右孩子 （2）有左孩子或者有右孩子  （3）既有左孩子又有右孩子。当然，每次删除节点后需要检查是否破坏了红黑树的结构，如果删除的节点是红色的，则删除后的树仍然保持红黑树的性质，因为没有改变每一条路径上的黑色节点的个数。如果删除的节点是黑色的，则删除后需要做一定的调整处理。

删除节点的伪代码：

RB_DELETE(T z)
    if left[z]==NIL||right[z]==NIL
        then y=z
    else y=TREE_SUCCESSOR(z)
    if left[z]!=NIL
        then x=left[z]
    else x=right[z]
    parent[x]=parent[y]
    if parent[y]==NIL
        then root[T]=x
    esle if y=left[parent[y]]
        then letf[parent[y]]=x
    else right[parent[y]]=x

    if y!=z
        then key[z]=key[y]
        copy y data to z data
    if color[y]=BLACK//当被删除的节点为黑色节点时进行调整
        then RB_DELETE_FIXEDUP(z)
    return y

 　　下面就看看删除操作后调整操作：如果包含两个子树并且被删除的节点为黑色，则有4种情况：

　　　　（1）x的兄弟w为红色

　　　　（2）x的兄弟w是黑色的，而且w的两个孩子都是黑色的

　　　　（3）x的兄弟w是黑色的，而且w的右孩子是红色的，左孩子是黑色的

　　　　（4）x的兄弟w是黑色的，而且w的左孩子是红色的，右孩子是黑色的

对于情况(1)：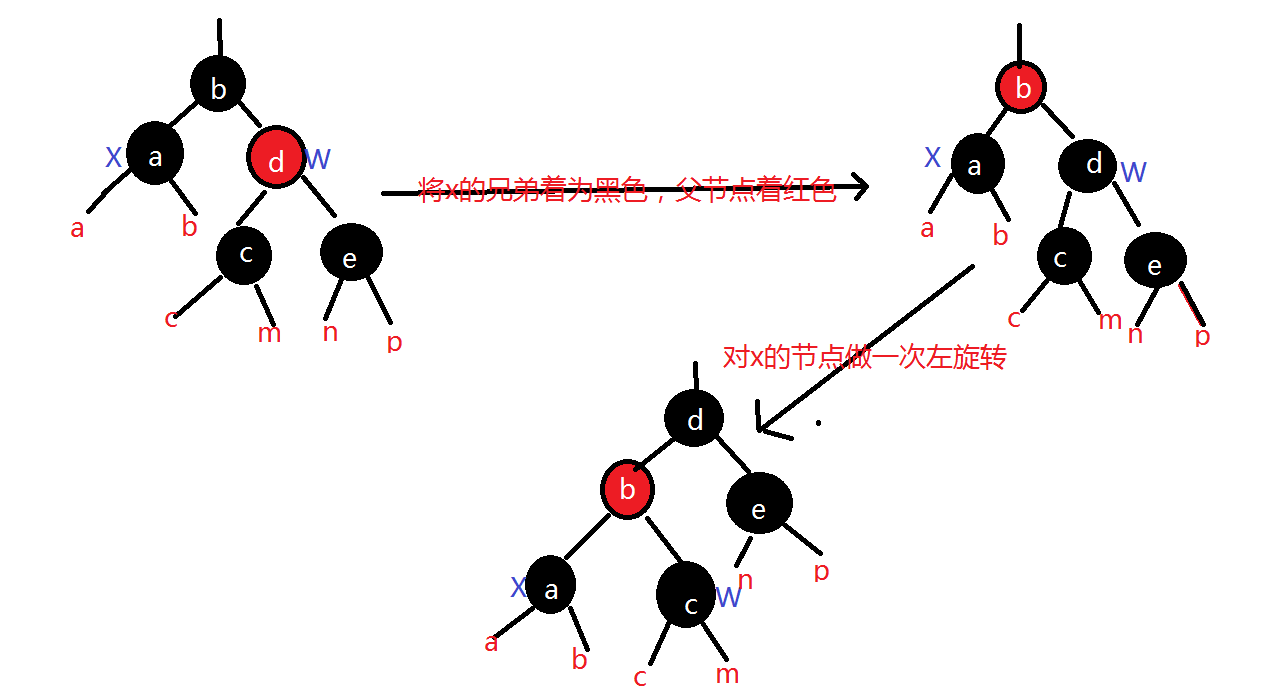

对于情况（2）：

对于情况（3）：

对于情况（4）：

对于删除的伪代码我就不粘贴了，如果想了解更多关于删除，我觉得这篇博客写的不错——红黑树的删除

　　最后经过一天半的学习，自我认为对红黑树有了相当的认识。红黑树在大神的眼里是在简单不过的了，但是对于我们这些初学者，还是有一定难度的，下面是我用c语言完成的代码，我发现网上有好多关于红黑树的文章及代码，但是如果我们不亲手写一遍就不会发现其中的乐趣，我也知道对于初学者代码规范是相当重要的，但是做起来没喇嘛容易。废话就不说了，红黑树算是完成了，敬请大神们勿笑。。。。。

代码：

#include <stdio.h>
#include <stdlib.h>
 typedef enum Color
 {
        RED   = 1,
        BLACK = 0
 }Color;
typedef struct Node
{
    struct Node *parent;  //父节点
    struct Node *left;    //左子树
    struct Node *right;   //右子树
    int          key;     //数据域
    Color        color;   //节点颜色
}Node,*RBTree;

void  rbInsert(RBTree *T,int key);//插入一个节点
Node *rbSearch(RBTree T,int key);//实现查找节点
void  rbDelete(RBTree *T,Node *z);//删除节点
Node *rbMinKey(RBTree T);//查找最小节点
Node *rbMaxKey(RBTree T);//查找最大的结点
void  rbPrint(RBTree T);//显示红黑树
static void InsertFixup(RBTree *T,Node *z);//插入节点后进行调整
static void DeleteFixup(RBTree *T,Node *x);//删除节点后进行调整
static Node *Parent(Node *x);
static Node *Left(Node *x);
static Node *Right(Node *x);
static void LeftRotate(RBTree *T, Node *x);//左旋
static void RightRotate(RBTree *T, Node *x);//右旋
static Node *RealDeleteNode(RBTree *T,Node *x);

static Node *nil = NULL;

static Node *Parent(Node *x)
{
     return x->parent;
}
static Node *Left(Node *x)
{
      return x->left;
}
static Node *Right(Node *x){
      return x->right;
}
static void LeftRotate(RBTree *T, Node *x)//左旋转：结点x原来的右子树y旋转成为x的父母
{
    if( x-> right != nil )
    {
        Node *y=Right(x);
        x->right=y->left;
        if(y->left != nil)
        {
            y->left->parent=x;
        }
        y->parent=x->parent;


        if( x->parent == nil )
        {
            *T=y;
        }
        else
        {
            if( x == Left(Parent(x)) )
            {
                x->parent->left=y;
            }
            else
            {
                x->parent->right=y;
            }
        }
        y->left=x;
        x->parent=y;
    }
}



static void RightRotate(RBTree *T, Node *x)   //右旋转：结点x原来的左子树y旋转成为x的父母
{
    if( x->left != nil )
    {
        Node *y=Left(x);
        x->left=y->right;
        if( y->right != nil )
        {
            y->right->parent=x;
        }
        y->parent=x->parent;
        if( x->parent == nil )
        {
            *T=y;
        }
        else
        {
            if(x == Left(Parent(x)) )
            {
                x->parent->left=y;
            }
            else
            {
                x->parent->right=y;
            }
        }
        y->right=x;
        x->parent=y;
    }
}
static Node *RealDeleteNode(RBTree *T,Node *x)//查找要删除的结点
{
        Node *p=x->right;
        while( p->left != nil )
        {
            p=p->left;

        }
        return p;
}

void rbInsert(RBTree *T,int key)
{
     if((*T)==NULL)
     {
        *T = (Node*)malloc(sizeof(Node));
        nil =(Node*)malloc(sizeof(Node));
        nil->color = BLACK;
        (*T)->parent = nil;
        (*T)->left   = nil;
        (*T)->right  = nil;
        (*T)->key  = key;
        (*T)->color  = BLACK;
     }else
     {
        Node *x = *T;
        Node *p = nil;
        while(x!=nil)
        {
            p = x;
            if(key>x->key)
                x = x->right;
            else if(key<x->key)
                x = x->left;
            else
                return ;
        }
        x = (Node*)malloc(sizeof(Node));
        x->parent = p ;
        x->left   = nil;
        x->right  = nil;

        x->key  = key;
        x->color  = RED;
        if(key<p->key)
        {
            p->left = x;
        }else
        {
            p->right = x;
        }
        InsertFixup(T,x);
     }
}

/*插入调整*/
static void InsertFixup(RBTree *T,Node *z)
{
     Node *y;
     while(Parent(z)->color == RED)
     {
        if(Parent(z) == Parent(Parent(z))->left)
        {
            y = Parent(Parent(z))->right;  //获取叔父结点
            if(y->color==RED)
            { //case 1  如果叔父结点为红色,则把父节点和叔父结点着黑,祖父结点着红,z上移到祖父结点
                y->color  = BLACK;
                z->parent->color = BLACK;
                z->parent->parent->color = RED;
                z = Parent(Parent(z));
            }
            else
            {
                if(z==Parent(z)->right)
                {   //case 2  如果叔父结点为黑色,z右结点,z上移为父亲结点,左旋转z结点,此时变为case3的情况
                    z = z->parent;
                    LeftRotate(T,z);
                }
                z->parent->color = BLACK;   //case 3 叔父结点为黑色,且z的左结点,z的父亲着着黑,z的祖父着红,然后旋转z的祖父结点
                Parent(Parent(z))->color = RED;
                RightRotate(T,Parent(Parent(z)));
            }
        }
        else
        {
           y = Parent(Parent(z))->left;
           if(y->color==RED)
           {
               y->color  = BLACK;
               z->parent->color = BLACK;
               z->parent->parent->color = RED;
               z = Parent(Parent(z));
           }
           else
            {
               if(z==Parent(z)->left)
               {
                  z = z ->parent;
                  RightRotate(T,z);
               }
               z->parent->color= BLACK;
               Parent(Parent(z))->color = RED;
               LeftRotate(T,Parent(Parent(z)));
           }
        }
     }
     (*T)->color = BLACK;
}
void rbDelete(RBTree *T,Node *z)
{
     if(z==nil || z==NULL)
            return ;
     Node *y;
     Node *x;
     if(z->left==nil || z->right ==nil)
     {
        y = z;
     }
     else
     {
        y = RealDeleteNode(T,z);
     }
     if(y->left!=nil)
        x = y->left ;
     else
        x = y->right;
     x->parent = y->parent;   //删除结点y
     if(y->parent==nil)
     {
        *T = x;
     }
     else
     {
        if(y==Parent(y)->left)
            y->parent->left = x;
        else
            y->parent->right = x;
     }
     if(y!=z)
     {
         z->key = y->key;
     }
     if(y->color==BLACK)
     {
        DeleteFixup(T,x);
     }
}
static void DeleteFixup(RBTree *T,Node *x)
{
     while(x!=(*T) && x->color==BLACK)
     {
        if(x==Parent(x)->left)
        {
            Node *w = Parent(x)->right;  //w 为x的兄弟结点
            if(w->color ==RED)
            {          //case 1 兄弟结点为红色
                w->color = BLACK;
                x->parent->color = RED;
                LeftRotate(T,Parent(x));
                w = Parent(x)->right;
            }
            if(w==nil) break;
            if(Left(w)->color ==BLACK && Right(w)->color==BLACK )
            {   //case2 兄弟结点的两个子结点都为黑
                w->color = RED;
                x = Parent(x);
            }
            else if(w->right->color ==BLACK)
            {    //case3 w的左子树为红色,右子树为黑色
                w->color = RED;
                w->left->color = BLACK;
                RightRotate(T,w);
                w = Parent(x)->right;
            }
            w->color = x->parent->color;         //case 4 w的右子树为红色
            x->parent->color = BLACK;
            w->right->color = BLACK;
            LeftRotate(T,Parent(x));
        }
        else
        {  //对称 调整同上
            Node *w= Parent(x)->left;
            if(w->color == RED)
            {
                w->color = BLACK;
                x->parent->color = RED;
                RightRotate(T,Parent(x));
                w = Parent(x)->left;
            }
            if(w==nil) break;
            if(Left(w)->color == BLACK && Right(w)->color == BLACK )
            {
                w->color = RED;
                x = Parent(x);
            }
            else if(w->left->color == BLACK)
            {
                w->color = RED;
                w->right->color = BLACK;
                LeftRotate(T,w);
                w = Parent(x)->left;
            }
            w->color = x->parent->color;
            x->parent->color = BLACK;
            w->left->color = BLACK;
            RightRotate(T,Parent(x));
        }
        x = *T;
     }
     x->color = BLACK;
}
Node *rbSearch(RBTree T,int key)
{
    if(T!=nil)
    {
        if(T->key<key)
            rbSearch(T->right,key);
        else if(T->key>key)
            rbSearch(T->left,key);
        else
            return T==nil ? NULL : T;
    }
}
void rbPrint(RBTree T)
{
     if(T!=NULL && T!=nil)
     {
        rbPrint(T->left);
        printf("%d(%s)\n",T->key,(T->color==RED) ? "红":"黑");
        rbPrint(T->right);
     }
}
Node *rbMinKey(RBTree T)
{
      Node *x=T;
      Node *p=nil;
      while(x!=nil)
      {
            p = x;
            x = x->left;
      }
      return p==nil ? NULL : p;
}
Node *rbMaxKey(RBTree T)
{
      Node *x=T;
      Node *p=nil;
      while(x!=nil)
      {
            p = x;
            x = x->right;
      }
      return p==nil ? NULL : p;
}
int main(int argc,char **argv)
{
    RBTree T=NULL;
    Node   *x;
    int a,b,c,d;
    printf("请输入你要插入的数据(注意数据输入的格式)：");
    while(scanf("%d",&a)!=EOF)
    {
        rbInsert(&T,a);
    }
    rbPrint(T);
    printf("max=%d\n",rbMaxKey(T)->key);
    printf("min=%d\n",rbMinKey(T)->key);
    printf("请输入你要输出的节点：\n");
    scanf("%d",&b);
    rbDelete(&T,rbSearch(T,b));
    rbPrint(T);
    printf("请输入你要插入的节点：\n");
    scanf("%d",&c);
    rbInsert(&T,c);
    rbPrint(T);
    return 0;
}