组合数

 

1.求阶乘

 

#include<cstdio>
const int N = 20;
const int MOD = 1e9 + 7;
int fac[N];
void init(){
    fac[0] = 1;
    for(int i=1; i<N-1; i++)
        fac[i] = fac[i-1] * i;
}
int main(){
    init();
}

 

2.求组合数

（1）直接按定义求

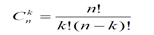
（2）递推公式求   下标加1上标取大

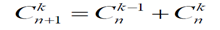
#include<cstdio>
const int N = 50;
const int MOD = (int)1e9 + 7;
int comb[N][N];//comb[n][m]就是C(n,m)
void init(){
    for(int i = 0; i < N; i ++){
        comb[i][0] = comb[i][i] = 1;
        for(int j = 1; j < i; j ++){
            comb[i][j] = comb[i-1][j] + comb[i-1][j-1];
        }
    }
}
int main(){
    init();
}

 

 

3.组合数取模

 

LL Comb(LL a,LL b, LL p)
{
    if(a < b) return 0;
    if(a == b) return 1;
    if(b > a-b) b = a-b;
    LL ans = 1, ca = 1, cb = 1;
    for(LL i=0; i<b; ++i)
    {
        ca = (ca*(a-i))%p;
        cb = (cb*(b-i))%p;
    }
    ans = (ca*Power_mod(cb, p-2, p))%p;
    return ans;
}

 

4.卢卡斯定理

 

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
LL Power_mod(LL a, LL b, LL p)
{
    LL res = 1;
    while(b!=0)
    {
        if(b&1) res = (res*a)%p;
        a = (a*a)%p;
        b >>= 1;
    }
    return res;
}
LL Comb(LL a,LL b, LL p)
{
    if(a < b) return 0;
    if(a == b) return 1;
    if(b > a-b) b = a-b;
    LL ans = 1, ca = 1, cb = 1;
    for(LL i=0; i<b; ++i)
    {
        ca = (ca*(a-i))%p;
        cb = (cb*(b-i))%p;
    }
    ans = (ca*Power_mod(cb, p-2, p))%p;
    return ans;
}
LL Lucas(int n, int m, int p)
{
    LL ans = 1;
    while(n && m && ans)
    {
        ans = (ans * Comb(n%p, m%p, p))%p;
        n /= p;
        m /= p;
    }
    return ans;
}
int main()
{
    int n,m,p;
    while(scanf("%d%d%d",&n,&m,&p) !=EOF)
    {
        printf("%lld\n",Lucas(n,m,p));
    }
    return 0;
}