LightOJ1234 Harmonic Number 调和级数求和

【题目】

 

【预备知识】

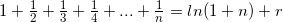，其中r是欧拉常数，const double r= 0.57721566490153286060651209;

这个等式在n很大 的时候 比较精确。

 

【解法】可以在 n较小的时候，比如n<1e6时，直接用预处理的打表O（1）求值，在n比较 大的时候，运用以上公式，此时要减去 1/（2*n）加以修正。

#include<iostream>
#include<cmath>
using namespace std;
const double euler= 0.57721566490153286060651209;
const int maxn = 1e6;
double a[maxn];
int cas = 1;
int main(){
    long long n;
    a[1] = 1;
    for(int i=2; i<maxn; i++){
        a[i] = a[i-1] + 1.0 / i;
    }
    int t;
    cin>>t;
    while(t--){
        cin>>n;
        if(n < maxn){
            printf("Case %d: %.10lf\n",cas++,a[n]);
            continue;
        }
        double ans = log(1+n) + euler - 1.0/(2*n);
        printf("Case %d: %.10lf\n",cas++,ans);
    }
    return 0;
} 

 

 

【分块打表】

虽然1e8的表打不出来，但1e6的表很好打，所以每隔100个数记录一次前缀和。到时用的时候，O（1）取出最接近n的前缀和，余下不足100个数暴力 求和即可。

 

#include<iostream>
#include<cmath>
using namespace std;
const double euler= 0.57721566490153286060651209;
const int maxn = 1e8+100;

double a[maxn/100];
int count = 1;

int cas = 1;
int main(){
    long long n;
    a[0] = 0;
    double s = 0;
    for(int i=1; i<maxn; i++){
        s += 1.0/i;
        if( i % 100 == 0){
            a[count++] = s;
        }
    }
    int t;
    cin>>t;
    while(t--){
        double ans = 0;
        cin>>n;
        int num = n / 100;//对应a[num]
        ans += a[num];
         for(long long i=num * 100 + 1; i<=n; i++){
             ans += 1.0/i;
         } 
         printf("Case %d: %.10lf\n", cas++, ans);
        
    }
    return 0;
}