筛表合集(素数筛 欧拉函数筛 莫比乌斯函数筛)
【目录】
一、素数筛
1.素数判断
2.素数普通筛
3.素数线性筛
4.素数区间筛
二、欧拉函数筛
三、莫比乌斯函数筛
【素数筛】
1.直接判定质数
bool judgePrime( int num ) { if(num < 2 ) return 0; int tmp =sqrt( num ); for(int i= 2; i <=tmp; i++) if(num % i == 0) return 0 ; return 1 ; }
2.素数普通筛
const int maxn = 1e7; bool isPrime[maxn+10]; int prime[maxn+10]; int count = 0; //普通筛法 void getPrime(){ memset(isPrime, 1, sizeof isPrime); isPrime[1] = isPrime[0] = 0; //筛出bool数组 for(int i=2; i*i<=maxn; i++){ //如果想在这里直接把素数打入prime数组里那么这里i<maxn if(isPrime[i]){ for(int j=2; j<=maxn/i; j++){ isPrime[i*j] = 0; } } } //根据bool数组把素数打入素数表 ,如果只要判断素数则以下代码可注释 // for(int i=0; i<maxn; i++){ // if(isPrime[i]) // prime[count++] = i; // } }
3.素数线性筛
保证每个素数只会被筛一次
//线性筛法 bool check[maxn + 10]; int prime2[maxn + 10]; int count2 = 0; void getPrime2(){ memset(check, 1, sizeof check); check[0] = check[1] = 0; for(int i=2; i<=maxn; i++){ if(check[i]){ prime2[count2++] = i; } for(int j=0; j<count2; j++){ if(i*prime2[j] > maxn) break; check[i*prime2[j]] = 0; if(i%prime2[j] == 0) break; } } }
4.素数区间筛
给定整数a和b,请问区间[a,b]内有多少个素数?
a<b<=10^12
b-a<=10^5
因为b以内合数的最小质因数一定不超过sqrt(b),如果有sqrt(b)以内的素数表的话,就可以把筛选法用在[a,b)上了.
先分别做好[2,sqrt(b)]的表和[a,b]的表,然后从[2,sqrt(b)]的表中筛得素数的同时,也将其倍数从[a,b)的表中划去,最后剩下的就是区间[a,b]内的素数了。
#include <cstdio> #include <cstring> #include <algorithm> using namespace std; typedef long long ll; const int maxn = 2e5+10; bool isPrimeSmall[maxn]; bool isPrimeBig[maxn]; ll getInterval(ll a, ll b){ memset(isPrimeSmall , 1 , sizeof isPrimeSmall); memset(isPrimeBig , 1 , sizeof isPrimeBig); isPrimeSmall[0] = isPrimeSmall[1] = 0; for(ll i = 2; i*i<b; i++){ if(isPrimeSmall[i]){ for(ll j=2*i; j*j<b; j+=i){ isPrimeSmall[j] = 0; } for(ll k = max(2LL, (a+i-1) / i) * i; k<=b; k+=i){ isPrimeBig[k - a] = 0; } } } ll ans = 0; for(ll i=0; i<= b-a; i++){ if(isPrimeBig[i]) ans ++; } if(a == 1) ans--;//防止1被当成质数 return ans; } int main() { ll a,b; int t; scanf("%d",&t); int cas = 1; while(t--) { scanf("%lld %lld",&a,&b); printf("Case %d: %lld\n",cas++, getInterval(a,b)); } return 0; }
小结:当需要频繁地判定素数时需要筛表,否则可以直接进行素数判断。筛表时,如果需要频繁地用素数而不是仅仅需要判定素数,用线性筛,否则用普通筛筛出bool数组即可。
筛表的范围,1e6基本无压力,1e7稍微有点大但能撑得住,1e8筛表速度很慢,1e9无法筛表,时间空间都跟不上。
注意:如果出现runtime error,可能是
int prime[maxn+10] 数组过大,可以先手动看一下count的值定这个数组的空间。
二、欧拉函数
欧拉函数的定义:
在数论中,对于正整数N,少于或等于N ([1,N]),且与N互质的正整数(包括1)的个数,记作φ(n)。
φ函数的值:
φ(x)=x(1-1/p(1))(1-1/p(2))(1-1/p(3))(1-1/p(4))…..(1-1/p(n)) 其中p(1),p(2)…p(n)为x的所有质因数;
1.直接判断
int Euler(int n){ int ans = n; //这里的n在不断收缩 循环次数上界将越来越小 for(int i=2; i<=n; i++){ if(n % i == 0){ ans = ans - ans/i; } //把该素因子除尽 while(n % i == 0) n = n/i; } return ans; }
2.欧拉函数筛表
筛表不太好理解,可以类比质数筛
(1)先锁定欧拉函数计算方法φ(x)=x(1-1/p(1))(1-1/p(2))(1-1/p(3))(1-1/p(4))…..(1-1/p(n)) 其中p(1),p(2)…p(n)为x的所有质因数;
(2)不妨初始化φ(x)=x
(3)每次遇到素因子的时候就乘上一个 p(i)-1 / p(i),p(i)是x的质因子
#define Max 1000 int euler[Max]; void Init(){ euler[1]=1;
for(int i=2;i<Max;i++) euler[i]=i; //初始化φ(x)=x for(int i=2;i<Max;i++) if(euler[i]==i) //这个欧拉值没有被更新过则需要更新,保证了进行更新时,i一定是素数 for(int j=i;j<Max;j+=i) euler[j]=euler[j]/i*(i-1);//先进行除法是为了防止中间数据的溢出 }
小结:
三、莫比乌斯函数筛
【莫比乌斯函数】µ(d)参考博客:https://blog.csdn.net/lixuepeng_001/article/details/50577932

【重要性质】

【反演公式】
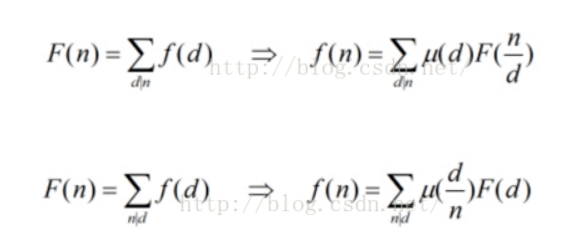
【莫比乌斯函数线性筛模板】
const int maxn=1000010; bool vis[maxn]; int prim[maxn]; int mu[maxn]; int cnt; void get_mu(){ mu[1]=1; for(int i=2;i<maxn;i++){ if(!vis[i]){ prim[++cnt]=i; mu[i]=-1; } for(int j=1;j<=cnt && prim[j]*i<maxn;j++){ vis[prim[j]*i]=1; if(i%prim[j]==0) break; else mu[i*prim[j]]=-mu[i]; } } }
【例题】HDU 1695
【AC代码】

#include<iostream> #include<cmath> #include<algorithm> using namespace std; typedef long long ll; const int maxn=1000010; bool vis[maxn]; int prim[maxn]; int mu[maxn]; int cnt; void get_mu(){ mu[1]=1; for(int i=2;i<maxn;i++){ if(!vis[i]){ prim[++cnt]=i; mu[i]=-1; } for(int j=1;j<=cnt && prim[j]*i<maxn;j++){ vis[prim[j]*i]=1; if(i%prim[j]==0) break; else mu[i*prim[j]]=-mu[i]; } } } ll a,b,c,d,k; int main(){ int t; cin>>t; get_mu(); int cas = 1; while(t--){ cin>>a>>b>>c>>d>>k; if(k > d || k > b || k == 0){ cout<<"Case "<<cas++<<": "<<0<<endl; continue; } b = b/k; d = d/k; ll ans1 = 0; ll ans2 = 0; for(int i=1; i<=min(b,d); i++){ ans1 += mu[i]*(b/i)*(d/i); } for(int i=1; i<=min(b,d); i++){ ans2 += mu[i]*(min(b,d)/i)*(min(b,d)/i); } cout<<"Case "<<cas++<<": "<<ans1 - (ans2>>1) <<endl; } }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号