斯皮尔曼+假设检验
例子
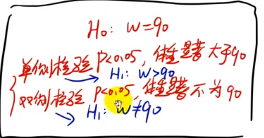
小明称体重发现自己有94斤,之前都是90的,小明想看看跟90有没有具体的差异。
- 90斤的条件下, W~N(90,4) 现在进行正态分布标准化 (w - 90)/ 2 ~ N(0,1)
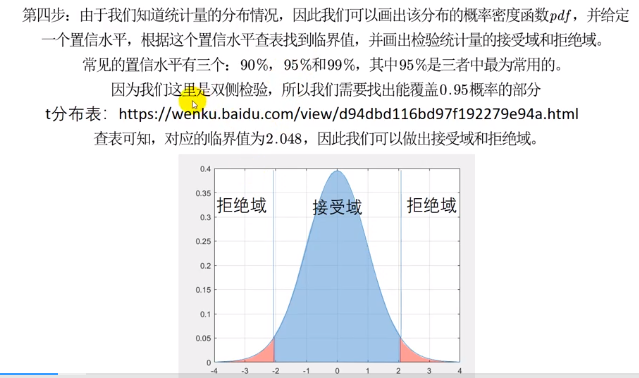
- 置信水平 95% 或者 99% ,Z~N(0,1) 且Z有95%的可能性位于区间接受域【-1.96,1.96】=0.95[1.96通过累积密度函数得来] 还有拒绝域
- 概率密度函数pdf => 离散型随机变量+ 连续型随机变量【 =1 】
https://blog.csdn.net/hhaowang/article/details/83898881
得出94斤拒绝原假设 如果置信区域设置在99% 无法拒绝
总结步骤
皮尔逊相关系数
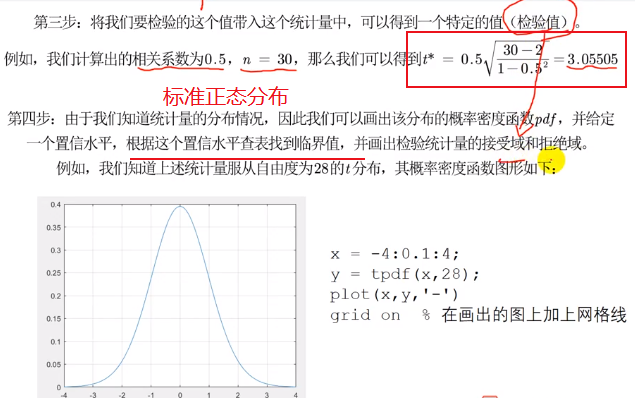
前两步
后两步
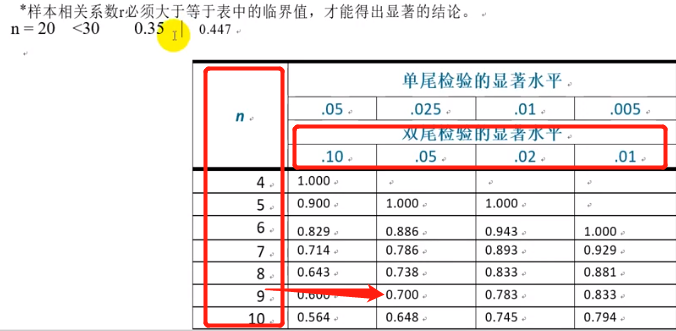
一般取95% 查表 临界值表 n 自由度
对N个随机样本而言,自由度df=n-k。其中n为样本数量,k为被限制的条件数或变量个数
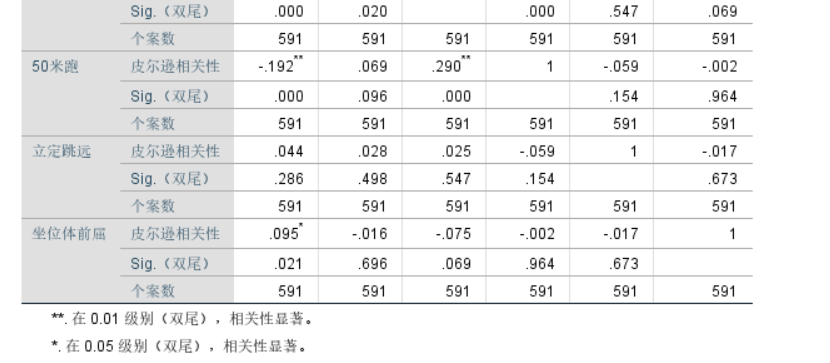
**的意思
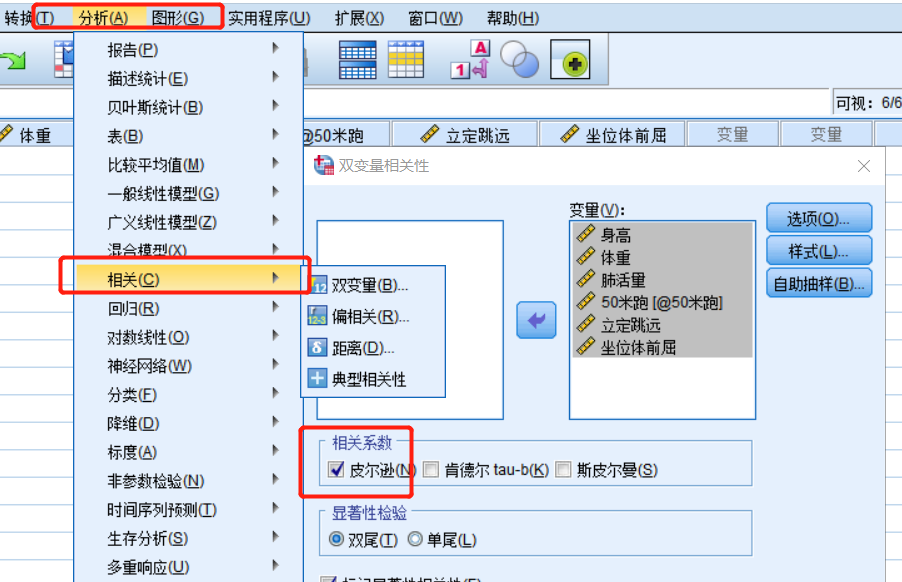
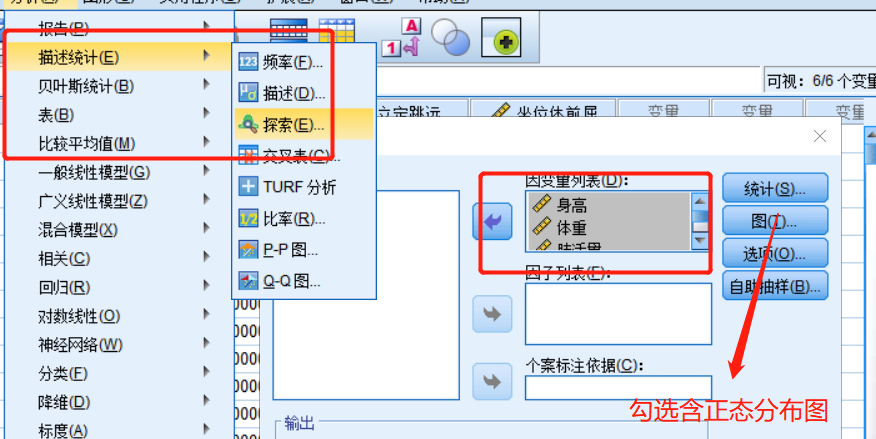
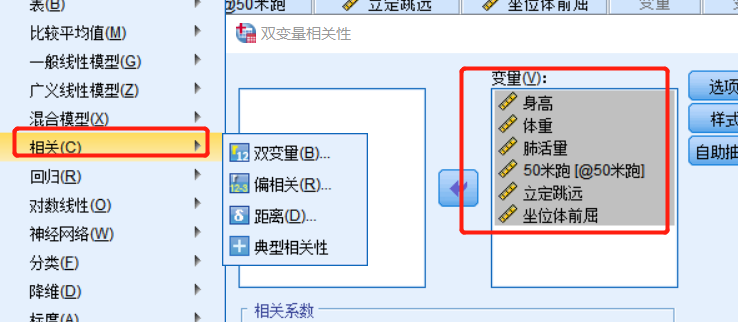
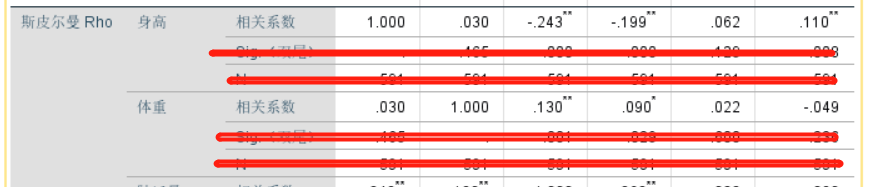
通过SPSS 软件也可进行皮尔逊相关系数分析
得到答案 可视化跟显著性二选一
条件
需要检验正态分布
正态分布JB检验 【n>30】
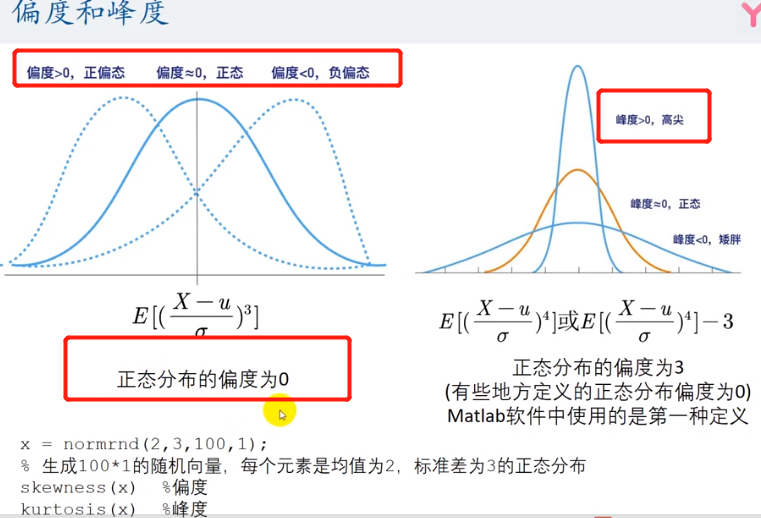
偏度的介绍
采用代码进行检验
[h , p ] = jbtest(Test(:,1),0.01) 都是1 拒绝原假设 不是正态分布 样本> 30
夏皮洛-威尔克检验 3 < n < 50
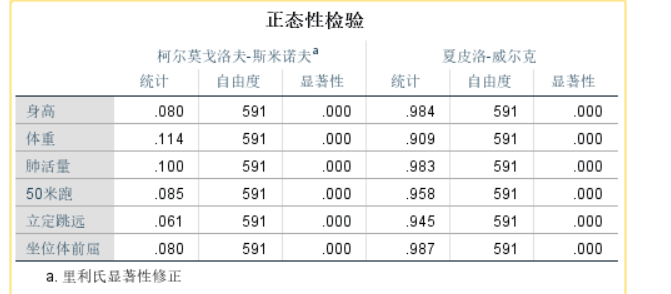
利用spss 软件
解得 最后一列为p值 看看接近0 不 为0拒绝原假设
Q_Q图 小样本不要用QQ图
qqplot
描述性统计 -> 正态性检验 如果没有通过检验 就用 斯皮尔曼系数
看散点图 看看有没有线性的趋势 有线性关系就可算出斯皮尔曼
需要用假设检验的话要 检验正态分布
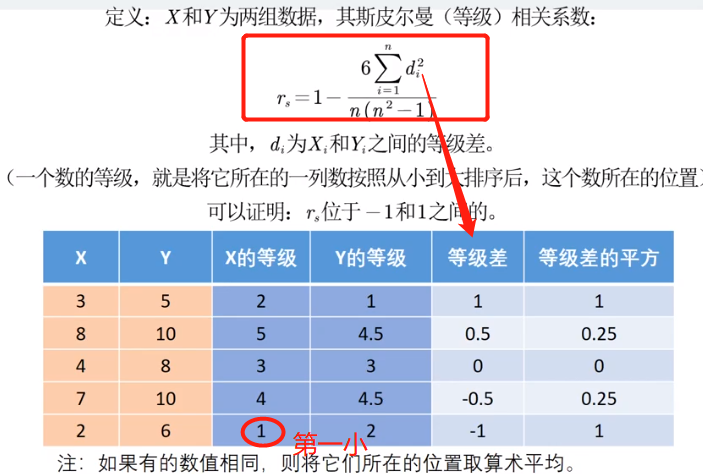
相同的话取平均值 大于0 正相关 小于0 负相关 越大相关性越强
第一种斯皮尔曼相关系数 被定义为等级之间的皮尔逊相关系数 行向量 微小差别为同值为同位
第二种 X 和 Y 都要为列向量 行向量运算为 NaN 异常
RX = [2 5 3 4 1];
RY = [1 4.5 3 4.5 2];
R = corrcoef(RX , RY)
RX = [3 8 4 7 2];
RY = [5 10 9 10 6 ];
R = corr(RX , RY , 'type','Spearman')
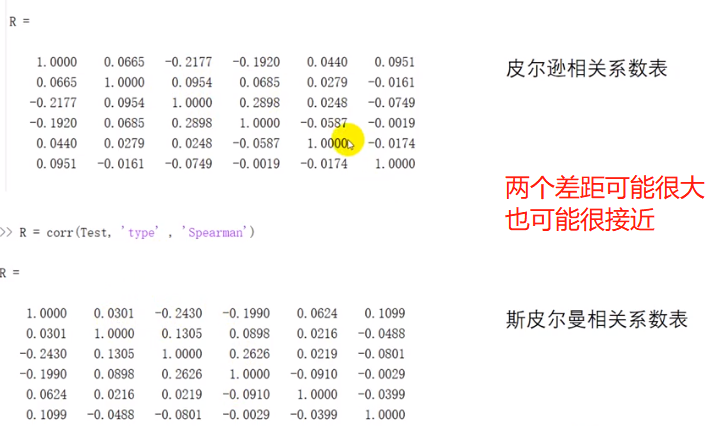
%两种答案相同说明 matlab 按照第二种皮尔逊那种进行计算
小样本 需要进行查表
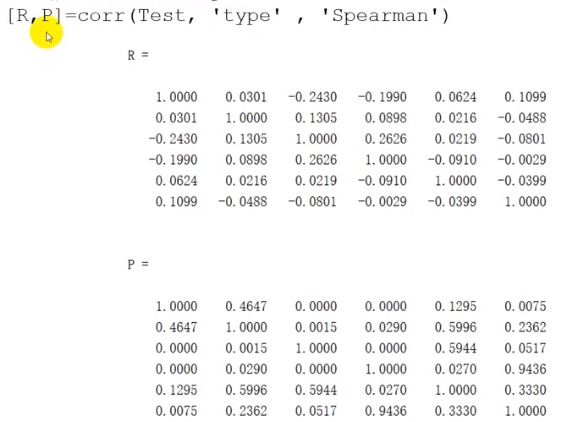
大样本
591 -> 样本数
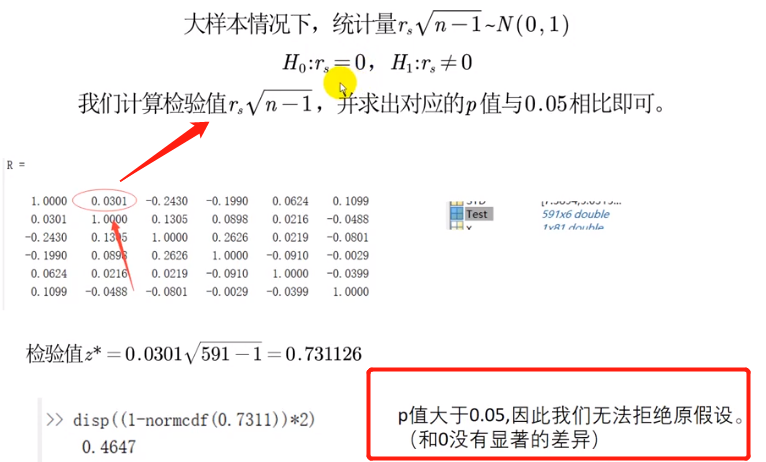
通过 (1- normcdf( R ) * 2) 得出
或者


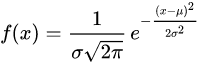










 浙公网安备 33010602011771号
浙公网安备 33010602011771号