2200.Eddys --数学组合

然后我百度一下找新的解决方法
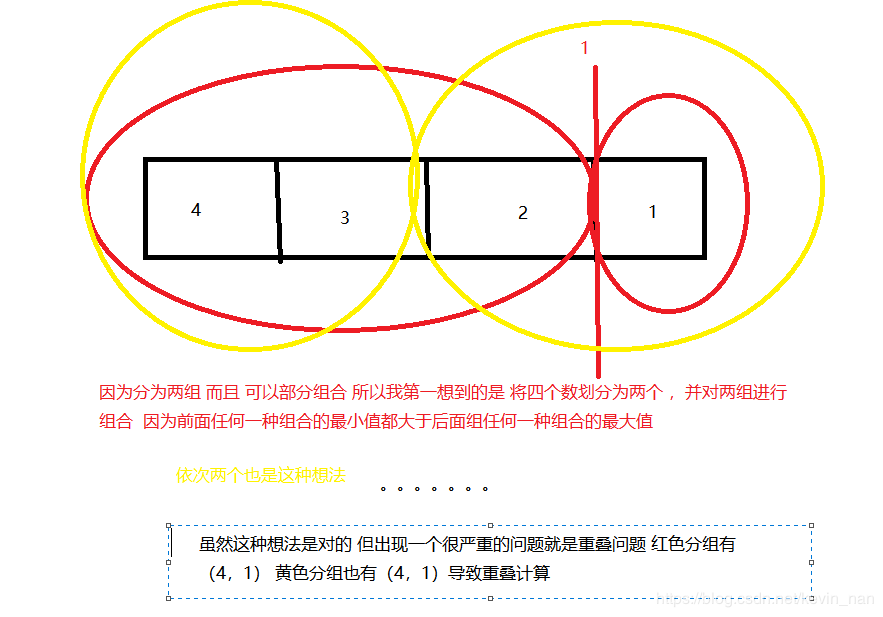
  可以这么想，假设n个人的ac数量按从小到大排列，可以从中任选m个人(n=>m>=2)，
  再把这m个人分2组(每个人都要分组)，要是满足最小ac数大于最大ac数，只需要在m
  个人中插板即可。例如： 
  m个人假如分别为 ： 
  1，2，3，4，......m-1，m (m个人的ac数从小到大排列) 
 只需在任意位置插板就可分为符合要求的2组： 
 1，2，3......t， || t+1...m-1，m (1<=t<m) 
 则 1，2，3......t 为一组 
 t+1，t+2，......m-1，m 为一组 
 很明显这样分组符合要求，在这m人中共有m-1种分法(t取不同值) 
得到解公式：f(n)=C(2,n)+C(3,n)2+……+C(k,n)(k-1)+……C(n,n)(n-1);
ps：C（X,X）M 这里M的是挡板的位置数 1|23 12|3 两种（两组都要有人 所以忽略 |123）

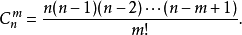
做这道题的坑 除法没保留小数点 溢出 公式代入出错

import java.text.DecimalFormat;
import java.util.Scanner;
public class Main {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		while (sc.hasNext()) {
			int n = sc.nextInt();
			double sum = 0;
			for (int i = 2; i <= n; i++) {
				sum += kMulC(i, n) * (i - 1);
			}
			DecimalFormat df = new DecimalFormat("0");
			System.out.println(df.format(sum));
		}
	}
	public static double kMulC(int m, int n) {
		double temp = 1;
		for (int i = 1; i <= m; i++) {
			temp *= i; // m!
		}
		double temp2 = 1;
		for (int i = n - m + 1; i <= n; i++) {
			temp2 *= i;
		}
		return temp2 / temp;
	}
}