1119考试总结
1119考试总结
T1
题目大意:
给定一个长度为 的数列 ,初始时数列中每个元素 都不大于 。你可以在其上进行若干次操作。在一次操作中,你会选出相邻且相等的两个元素,把它们合并成一个元素,新的元素值为 (旧 元 素 值 + 1)。
请你找出,怎样的一系列操作可以让数列中的最大值变得尽可能地大?这个最大值是多少? \(n <= 2^{18}, a <= 40\)
题目链接
\(f[i][j]\), 表示\(i\)这个位置可以合成\(j\)这个数字, 并且后继为\(f[i][j]\)."后继"就是指合成\(j\)这一段区间的右端点的下一位.
然后我们可以知道, 如果\(f[i][j - 1], f[f[i][j - 1]][j - 1]\)可以被合成, 那么\(f[i][j]\)也可以被合成, 然后使\(f[i][j] = f[f[i][j - 1]][j - 1]\).
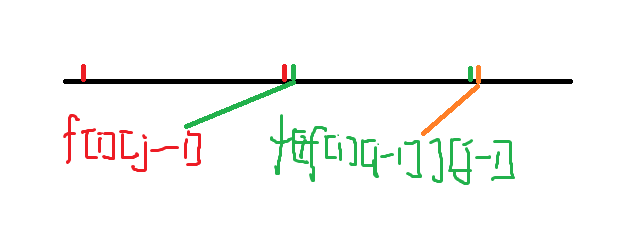
如上图, 红色的那一段可以合成\(j\), \(f[i][j - 1]\)存的是红色合成区间右端点的下一个位置, 也就是绿色部分的合成区间的左端点.
#include <bits/stdc++.h>
using namespace std;
inline long long read() {
long long s = 0, f = 1; char ch;
while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
for(s = ch ^ 48;isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
return s * f;
}
const int N = 3e5 + 5;
int n, ans;
int f[N][70];
int main() {
n = read();
for(int i = 1;i <= n; i++) f[i][read()] = i + 1;
for(int j = 1;j <= 60; j++)
for(int i = 1;i <= n; i++)
if(f[i][j - 1] && f[f[i][j - 1]][j - 1]) f[i][j] = f[f[i][j - 1]][j - 1], ans = j;
printf("%d", ans);
return 0;
}
T2
题目大意:
定义函数\(f(n)\)为选取两个小于\(n\)的非负整数 ,使得\(a *b\)不是\(n\)的倍数的方案数。
定义函数\(g(n) = \displaystyle \sum_{d \mid n} f(d)\)现给出多组询问,每组询问给出一个正整数\(n\), 请回答\(g(n)\)的值。 \(n <= 1e9, T <= 1e4\)
莫比乌斯反演.
首先推导\(f(n)\):
\(f(n) = \displaystyle n ^ 2 - \sum_{a = 1}^{n}\sum_{b = 1}^{n}[n \mid ab]\) 这一句是简化题意.
\(f(n) = \displaystyle n ^ 2 - \sum_{a = 1}^{n}\sum_{b = 1}^{n}[\frac{n}{gcd(a, n)} \mid \frac{ab}{gcd(a, n)}] = n ^ 2 - \sum_{a = 1}^{n}\sum_{b = 1}^{n}[\frac{n}{gcd(a, n)} \mid b]\), 首先\(n\)整除\(ab\), 那么他俩同时除以\(gcd(a,n)\)依然成立, 又发现\(\frac{n}{gcd(a, n)} \frac{a}{gcd(a, n)}\) 互质, 那么可以得到\(\frac{n}{gcd(a, n)} \mid b\).
\(f(n) = \displaystyle n ^ 2 - \sum_{a = 1}^{n}gcd(a, n)\), 这里可以理解为\(1\)到\(n\)中有几个数字是\(\frac{n}{gcd(a,n)}\)的倍数, 也就是有\(\displaystyle \frac{n}{\frac{n}{gcd(a,n)}} = gcd(a,n)\)个.
然后开始反演:
\(f(n) = \displaystyle n ^ 2 - \sum_{a = 1}^{n}gcd(a, n) = n ^ 2 - \sum_{d\mid n} d \sum_{a = 1}^{n} [gcd(a, n) == d] = n ^ 2 - \sum_{d\mid n} d \sum_{a = 1}^{n / d} [gcd(a, n/d) == 1] = n ^ 2 - \sum_{d\mid n} d \sum_{a = 1}^{n / d} \sum_{q \mid gcd(a, n/d)} \mu(q)\)
\(f(n) = \displaystyle n ^ 2 - \sum_{d\mid n} \sum_{q\mid \frac{n}{d}} d *\mu(q) \sum_{a = 1}^{n / d} [q \mid a] = n ^ 2 - \sum_{d\mid n} \sum_{q\mid \frac{n}{d}} \mu(q) id(\frac{n}{d} / q) * \frac{d^2q}{n} * \frac{n}{dq} = n ^ 2 - \sum_{d\mid n} \phi(n / d) * d\)
然后的然后推导\(g(n)\):
\(\displaystyle g(n) = \sum_{d \mid n} f(d) = \sum_{d \mid n}d^2 - \sum_{d \mid n}\sum_{q \mid d}\phi(d/q)*q = \sum_{d \mid n}d^2 - \sum_{d \mid n} \phi(d)*id(d) = \sum_{d \mid n}d^2 - \sum_{d \mid n}1(n / d)(\phi(d)*id(d)) = \sum_{d \mid n}d^2 - 1(n)(\phi(n)*id(n))\)
\(g(n) = \displaystyle \sum_{d \mid n}d^2 - id(n)*id(n) = \sum_{d \mid n}d^2 - \sum_{d \mid n} id(d) * id(n / d) = \sum_{d \mid n}d^2 - \sum_{d \mid n} d * n / d = \sum_{d \mid n}d^2 - \sum_{d \mid n} n\)
然后\(g(n)\)就可以\(O(\sqrt n)\)求啦.
复杂度\(O(T\sqrt n)\).
#include <bits/stdc++.h>
using namespace std;
inline long long read() {
long long s = 0, f = 1; char ch;
while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
for(s = ch ^ 48;isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
return s * f;
}
long long calc(int d, int n) { return 1ll * d * d - n; }
void work(int n) {
long long res = 0; register int i;
for(i = 1;i * i < n; i++) if(!(n % i)) res += calc(i, n), res += calc(n / i, n);
if(i * i == n) res += calc(i, n);
printf("%lld\n", res);
}
int main() {
for(int T = read(); T ; T --) work(read());
return 0;
}
T3
题目大意:
你想送给 Makik 一个情人节礼物,但是手中只有一块方格纸。这张方格纸可以看作是一个由\(n\)行\(m\)列格子组成的长方形,不幸的是上面甚至还有一些格子(\(P\)个)已经损坏了。为了让这张破破烂烂的方格纸变得像个礼物的样子,你要从中剪出一个边长不小于\(l\)的方框,并且损坏的格子都不能被包含在这个方框中。这里,一个边长为\(s\)的方框指的是大小为\(s\)的正方形最外层的\(4*(s - 1)\)个格子所构成的形状。在动手剪方格纸之前,请你算一算一共有可能剪出多少种不同的方框?
$ n, m <= 4000, P <= 100000$
树状数组 + 离散化 + 前缀和 + 差分.
首先我们可以预处理出一个格子\((i,j)\)向左, 向右, 向上, 向下可以延伸多少格子没有障碍, 分别用\(f1[i][j], f2[i][j], f3[i][j], f4[i][j]\)表示.
然后我们让\(f1, f3\)合并, \(f1[i][j] = min(f1[i][j], f3[i][j])\), 让\(f1[i][j]\)表示向左上可以延伸多少格子, \(f2, f4\)同理, \(f2\)表示向右下可以延伸多少格子.
为什么要预处理这些呢? 我们知道要取出的合理部分应该是一个正方形, 那么我们可以用一条对角线来确定每一个正方形, 那我们就可以枚举一个正方形的对角线的左上角和右下角的端点, 这样就可以确定一个正方形.
单纯的枚举然后再检验是否有损坏肯定是不行的, 当我门枚举到一个右下端点时, 左上端点的合法位置其实可以用前缀和统计的, 这时候就要用到树状数组来维护这个前缀和.
对于每个右下端点, 我们可以更新的左上端点其实是一段区间, 用差分来修改可以很方便.每当我们枚举到一个右下端点时, 我们将之前记录的左上端点的差分修改到树状数组里(相当于是懒标记), 然后统计前缀和, 最后再把这个右下端点作为左上端点时对应的右下区间存起来, 等到后面差分用.(说的很乱, 具体可以看代码)
#include <bits/stdc++.h>
using namespace std;
inline long long read() {
long long s = 0, f = 1; char ch;
while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
for(s = ch ^ 48;isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
return s * f;
}
const int N = 4005, M = 1e5 + 5;
int n, m, l, p;
int f1[N][N], f2[N][N], f3[N][N], f4[N][N];
long long ans, t[N];
bool vis[N][N];
vector <pair<int, int> > v[N];
void make_pre() {
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j++)
if(!vis[i][j]) {
f1[i][j] = f1[i][j - 1] + 1;
f3[i][j] = f3[i - 1][j] + 1;
}
for(int i = n;i >= 1; i--)
for(int j = m;j >= 1; j--)
if(!vis[i][j]) {
f2[i][j] = f2[i][j + 1] + 1;
f4[i][j] = f4[i + 1][j] + 1;
}
for(int i = 1;i <= n; i++)
for(int j = 1;j <= m; j++) {
f1[i][j] = min(f1[i][j], f3[i][j]);
f2[i][j] = min(f2[i][j], f4[i][j]);
}
}
int lowbit(int x) { return x & -x; }
void change(int x, int y) { for(; x < N ; x += lowbit(x)) t[x] += y; return ; }
long long query(int x) { long long res = 0; for(; x ; x -= lowbit(x)) res += t[x]; return res; }
int main() {
n = read(); m = read(); l = read(); p = read();
for(int i = 1, x, y;i <= p; i++) x = read(), y = read(), vis[x][y] = 1;
make_pre();
for(int x = n, y = 1;y <= m; x == 1 ? y ++ : x --) { //枚举每一条对角线
int len = 0; memset(t, 0, sizeof(t));
for(int i = 1;i <= max(n, m); i++) v[i].clear();
for(int i = x, j = y;i <= n && j <= m; i++, j++) len ++; // 把这条对角线拉出来
for(int i = 1;i <= len; i++) {
for(int j = 0;j < (int)v[i].size(); j++) change(v[i][j].first, v[i][j].second); // 懒标记更新
if(f1[i + x - 1][i + y - 1] >= l) ans += query(i - l + 1) - query(i - f1[i + x - 1][i + y - 1]); // 当前点作为右下端点
if(f2[i + x - 1][i + y - 1] >= l) v[i + l - 1].push_back(make_pair(i, 1)), v[i + f2[i + x - 1][i + y - 1]].push_back(make_pair(i, -1)); // 当前点作为左上端点
}
}
printf("%lld", ans);
return 0;
}


