0926考试T3 容斥原理+组合数学

0926考试T3

​

​ 题目大意：

​

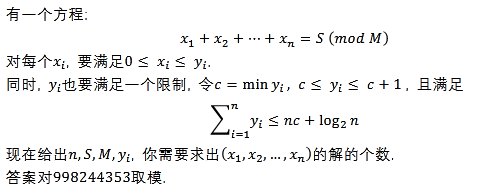
​ \(n \le 10 ^ 5, 10 ^ 5 \le m \le 10^9, y_i \le 50, 0 \le S \le min(M,\sum y_i)\)

​

​ 容斥原理 + 组合数学。

​

​ 一开始看到这题很蒙啊，根本不知道从哪去想，于是就写了个爆搜。

​ 我就直接粘题解吧，稍微解释一下。

​

​ 把集合根据大小分类那个式子：当\(i = 0\)时，\(f(H)\)不就是所有\(x >= 0\)的时候吗，那相当于没有任何限制，是所有情况。当\(i = 1\)时，\(f(H)\)是一个数一定不满足的情况，给他减去，然后以此类推，两个数的时候再加上。

​ \(f(H)\)的取值咋解释呢？你可以理解为\(S\)个1，要把它分为\(n\)个数，这\(n\)个数可以为0，所以在给它加\(n\)个1。有\(S +n\)个1，就有\(s + n - 1\)个间隙，\(n - 1\)个板将他们分成\(n\)个数。这\(n\)个数有属于\(H\)的有不属于的。对于那些属于\(H\)的，它需要满足\(x_i > y_i\)，所以这\(S + n\)个1还要再减去\(\sum _{i \subseteq H} (y_i + 1)\)个1。加一是因为\(y_i + 1\)一定可以满足\(x_i > y_i\)的条件。

​ 底下那个化简：\(m\)为\(c+1\)的个数，\(i\)为集合元素个数，枚举\(j <= m, j <= i\)，\(-j-i(c+1)\)就是有集合中有\(i\)个数，给其中的\(j\)个数\(+1\)。

#include <bits/stdc++.h>

using namespace std;

inline long long read() {
    long long s = 0, f = 1; char ch;
    while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
    for(s = ch ^ 48;isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
    return s * f;
}

const int N = 6e6 + 5, mod = 998244353;
int n, s, m, c, ans, sum;
int y[N], fac[N], inv[N];

void make_pre() {
    fac[0] = fac[1] = inv[0] = inv[1] = 1;
    for(int i = 2;i <= N - 5; i++) fac[i] = 1ll * fac[i - 1] * i % mod;
    for(int i = 2;i <= N - 5; i++) inv[i] = 1ll * (mod - mod / i) * inv[mod % i] % mod;
    for(int i = 2;i <= N - 5; i++) inv[i] = 1ll * inv[i - 1] * inv[i] % mod;
}

int C(int x, int y) {
    if(x < y) return 0;
    return 1ll * fac[x] * inv[y] % mod * inv[x - y] % mod; 
}

int calc(int s, int m) {
    int res = 0;
    for(int i = 0;i <= n; i++) {
        int tmp = 0;
        for(int j = 0;j <= m && j <= i; j++) {
            (tmp += 1ll * C(s - j - i * (c + 1) + n - 1, n - 1) * 
             C(m, j) % mod * C(n - m, i - j) % mod) %= mod;
        }
        if(i & 1) res = (res - tmp + mod) % mod;
        else res = (res + tmp) % mod;
    }
    return res;
}

int main() {

    n = read(); s = read(); m = read();
    make_pre(); c = 51;
    for(int i = 1;i <= n; i++) y[i] = read(), sum += y[i], c = min(c, y[i]);
    
    for(int i = s;i <= sum; i += m) 
        ans = (ans + calc(i, sum - c * n)) % mod;
    
    printf("%lld", ans);

    
    fclose(stdin); fclose(stdout);
    return 0;
}