0922考试T3 dfs序 lca 线段树 树上问题

0921考试T3

​ 题目描述：

​ 在暑假来临之际，小Z的地理老师布置了一个暑假作业，让同学们暑假期间了解一下C国的铁路发展史。小Z在多番查证资料后发现，C国在铁路发展初期，铁路网络有着一个严密规整的结构：C国的N个城市按层级分为首都、省会、省辖市......由于在铁路发展初期，建造铁路花费巨大，为了避免不必要的浪费，铁路网络的建设保证了任意两个城市相互连通，且仅有一条连通路径。随后，小Z还查阅到历年来铁道部向全国上下发布的大小消息。由于多年来C国货币系统保持健康的3%通胀率带来了稳定的物价上涨，铁道部发布的消息中不乏对某段连接城市u与城市v铁路的价格上涨w元的通知。于是小Z不禁好奇，在某些特定时间，在某个城市p的管辖区域内，任意两个城市间的铁路通勤的费用和是多少。

​ 第一行输入两个正整数N，Q，分别表示城市的数目和操作的数目。接下来有N–1行，第i行是两个正整数p[i],c[i]，表示城市p[i]是城市i的父亲结点，且连接p[i]和i的铁路的初始收费为c[i]（1≤c[i]≤1000）。

​ 再接下来有Q行，每行是如下两种类型之一：INC u v w(u,v,w都是整数，且1≤u,v≤N,0≤w≤1000) ASK p(p是整数，且0≤p≤N)意义如题目所述。

​ 树剖可做，dfs序也可做。但dfs序好做。

​

​ 设\(x\)与它的父亲\(fa[x]\)相连的边的边权为\(p[x]\)。那么这条边对整棵树的贡献就是\(p[x] *siz[x] *(siz[root] - siz[x])\)。

​ 我们把这个式子拆开\(p[x] * siz[x] * siz[root] - p[x] * siz[x] ^ 2\)，发现很多部分与\(root\)无关。

​ 我们现在如果要算\(root\)的子树内的答案，那么就是：\(siz[root]*\sum p[x] *siz[x] - \sum p[x] * siz[x] ^ 2\)。

​ 那怎么修改呢？我们写出一颗树的dfs序（其实也不太严谨），举个例子：

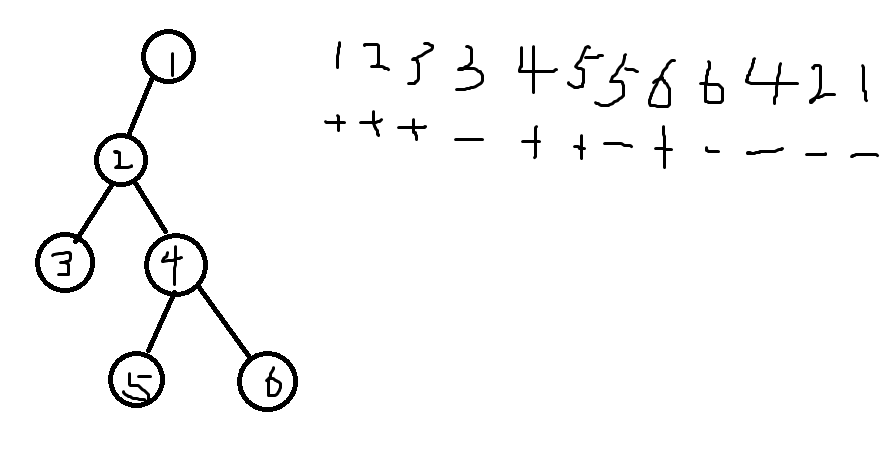
​ 像上图，第一次出现的数我们把它标为正，第二次出现的标为负，现在我们如果想修改\(6\)到\(2\)路上的边，那么我们只需找到\(2,6\)第一次出现的位置\(x, y\)，对区间\([x +1, r]\)进行修改就好了，你会发现中间出现两次的点其实并没有修改，一加一减抵消了，所以最终我们只修改了\(p[4], p[6]\)。

​ 然后就可做了，先把dfs序搞出来，再用用线段树维护一段区间的\(\sum p[x] *siz[x], \sum p[x] * siz[x] ^ 2\)。修改树上两个点的时候还得求一下\(lca\)。

#include <bits/stdc++.h>

#define ls(o) (o << 1)
#define rs(o) (o << 1 | 1)
#define mid ((l + r) >> 1)

using namespace std;

inline long long read() {
    long long s = 0, f = 1; char ch;
    while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
    for(s = ch ^ 48;isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
    return s * f;
}

const int N = 5e4 + 5, mod = 2019;
int n, m, cnt;
int v[N], val[N << 1], dep[N], siz[N], fa[N], f[N][21], sum1[N << 1], sum2[N << 1];
vector <int> edge[N];
struct P { int fi, se; } p[N];
struct tree { int s1, s2, add; } t[N << 3];

void get_tree(int x) {
    val[++cnt] = x; p[x].fi = cnt; siz[x] = 1;
    for(int i = 0; i < (int) edge[x].size() ; i ++) {
        int y = edge[x][i];
        dep[y] = dep[x] + 1;
        get_tree(y);
        siz[x] += siz[y];
    }
    val[++cnt] = -x; p[x].se = cnt;
}

void modify(int o, int l, int r, int k) {
    t[o].s1 =(t[o].s1 + 1ll * (sum1[r] - sum1[l - 1]) * k % mod) % mod;
    t[o].s2 =(t[o].s2 + 1ll * (sum2[r] - sum2[l - 1]) * k % mod) % mod;
    t[o].add = (t[o].add + k) % mod;
}

void down(int o, int l, int r) {
    if(t[o].add) modify(ls(o), l, mid, t[o].add), modify(rs(o), mid + 1, r, t[o].add), t[o].add = 0;
}

void up(int o) {
    t[o].s1 = (t[ls(o)].s1 + t[rs(o)].s1) % mod;
    t[o].s2 = (t[ls(o)].s2 + t[rs(o)].s2) % mod;
}

void change(int o, int l, int r, int x, int y, int val) {
    if(x <= l && y >= r) { modify(o, l, r, val); return ; }
    down(o, l, r);
    if(x <= mid) change(ls(o), l, mid, x, y, val);
    if(y > mid) change(rs(o), mid + 1, r, x, y, val);
    up(o);
}

pair <int, int> query(int o, int l, int r, int x, int y) {
    if(x <= l && y >= r) return make_pair(t[o].s1, t[o].s2);
    pair <int, int> res1 = make_pair(0, 0), res2 = make_pair(0, 0);
    down(o, l, r);
    if(x <= mid) res1 = query(ls(o), l, mid, x, y);
    if(y > mid) res2 = query(rs(o), mid + 1, r, x, y);
    return make_pair((res1.first + res2.first) % mod, (res1.second + res2.second) % mod);
}

void make_pre() {
    get_tree(1);

    for(int i = 1;i <= cnt; i++) {
        int r = val[i];
        if(r > 0) {
            sum1[i] = (sum1[i - 1] + siz[r] % mod) % mod;
            sum2[i] = (sum2[i - 1] + 1ll * siz[r] * siz[r] % mod) % mod;
        }
        else {
            r = -r;
            sum1[i] = (sum1[i - 1] - siz[r] + mod) % mod;
            sum2[i] = (sum2[i - 1] - 1ll * siz[r] * siz[r] + mod % mod) % mod;
        }
    }

    for(int i = 1;i <= n; i++) f[i][0] = fa[i];
    for(int i = 1;i <= 20; i++)
        for(int j = 1;j <= n; j++) f[j][i] = f[f[j][i - 1]][i - 1];
    for(int i = 2;i <= n; i++) change(1, 1, cnt, p[i].fi, p[i].fi, v[i]);
}

int LCA(int x, int y) {
    if(dep[x] < dep[y]) swap(x, y);
    for(int i = 20;i >= 0; i--) 
        if(dep[x] - dep[y] >= (1 << i)) x = f[x][i];
    if(x == y) return x;
    for(int i = 20;i >= 0; i--)
        if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
    return f[x][0];
}

void change_path(int x, int y, int w) {
    if(x == y) return ; 
    int lca = LCA(x, y);
    if(y == lca) swap(x, y);
    if(x == lca) {
        change(1, 1, cnt, p[lca].fi + 1, p[y].fi, w);
    }
    else {
        change(1, 1, cnt, p[lca].fi + 1, p[x].fi, w);
        change(1, 1, cnt, p[lca].fi + 1, p[y].fi, w);
    }
}

int main() {

    n = read(); m = read();
    for(int i = 2;i <= n; i++) {
        fa[i] = read(); v[i] = read(); edge[fa[i]].push_back(i);
    }

    make_pre();

    for(int i = 1, u, v, w;i <= m; i++) {
        char opt[4]; cin >> opt;
        if(opt[0] == 'A') {
            u = read();
            pair <int, int> tmp = query(1, 1, cnt, p[u].fi + 1, p[u].se - 1);
            int res = (siz[u] * tmp.first - tmp.second + mod) % mod;
            res = (res + mod) % mod;
            printf("%d\n", res);
        }
        else {
            u = read(); v = read(); w = read(); 
            change_path(u, v, w);
        }
    }

    fclose(stdin); fclose(stdout);
    return 0;
}