P3345 [ZJOI2015]幻想乡战略游戏

题目描述

傲娇少女幽香正在玩一个非常有趣的战略类游戏，本来这个游戏的地图其实还不算太大，幽香还能管得过来，但是不知道为什么现在的网游厂商把游戏的地图越做越大，以至于幽香一眼根本看不过来，更别说和别人打仗了。在打仗之前，幽香现在面临一个非常基本的管理问题需要解决。整个地图是一个树结构，一共有 n 块空地，这些空地被 n−1 条带权边连接起来，使得每两个点之间有一条唯一的路径将它们连接起来。

在游戏中，幽香可能在空地上增加或者减少一些军队。同时，幽香可以在一个空地上放置一个补给站。如果补给站在点 u 上，并且空地 v 上有 dv 个单位的军队，那么幽香每天就要花费 dv×dist(u,v) 的金钱来补给这些军队。由于幽香需要补给所有的军队，因此幽香总共就要花费为 ∑(dv×dist(u,v))（其中1≤v≤N）的代价，dist(u,v) 表示 u 个 v 在树上的距离（唯一路径的权和）。因为游戏的规定，幽香只能选择一个空地作为补给站。在游戏的过程中，幽香可能会在某些空地上制造一些军队，也可能会减少某些空地上的军队，进行了这样的操作以后，出于经济上的考虑，幽香往往可以移动他的补给站从而省一些钱。但是由于这个游戏的地图是在太大了，幽香无法轻易的进行最优的安排，你能帮帮她吗？你可以假定一开始所有空地上都没有军队。

输入格式

第一行两个数 n 和 Q 分别表示树的点数和幽香操作的个数，其中点从 1 到 n 标号。

接下来 n−1 行，每行三个正整数 a,b,c，表示 a 和 b 之间有一条边权为 c 的边。

接下来 Q 行，每行两个数 u,e，表示幽香在点 u 上放了 e 单位个军队（如果 e<0，就相当于是幽香在 u 上减少了 ∣e∣ 单位个军队，说白了就是 du←du+e）。

数据保证任何时刻每个点上的军队数量都是非负的。

输出格式

对于幽香的每个操作，输出操作完成以后，每天的最小花费，也即如果幽香选择最优的补给点进行补给时的花费。

输入输出样例

输入 #1

输出 #1

说明/提示

对于所有数据，\(1≤c≤10^3，0≤∣e∣≤10^3，1≤n≤10^5，1≤Q≤10^5\)

非常神奇的是，对于所有数据，这棵树上的点的度数都不超过 20。

动态点分治的题。

\(sum_x\)：表示\(x\)这颗树内的\(d\)值之和。

\(dum_x\)：表示\(x\)这颗树内的\(d *dis(x, y)\)值之和。

\(fum_x\)：表示\(x\)这颗树内的\(d *dis(fa[x], y)\)值之和。

（其中\(y\)为\(x\)的子树内的节点，\(fa[x]\)为\(x\)在点分树上的父亲）

我们可以发现其实可以通过贪心的方法找到最小的\(ans\)，我们假设一开始在\(x\)，那么遍历它所有的儿子\(y\)，以\(y\)作为补给点找答案，哪个小就往那里走。如果所有\(y\)的\(ans\)都大于以\(x\)为补给点的\(ans\)，那么\(x\)就是当前最合适的补给点。

假设现在以\(x\)点为补给点，计算\(ans\)的方法：

long long calc(int x) {
    long long res = dum[x];
    for(int i = x; fa[i]; i = fa[i]) 
        res += dum[fa[i]] - fum[i] + (sum[fa[i]] - sum[i]) * dist(fa[i], x); //画个图就好理解了
    return res;
}

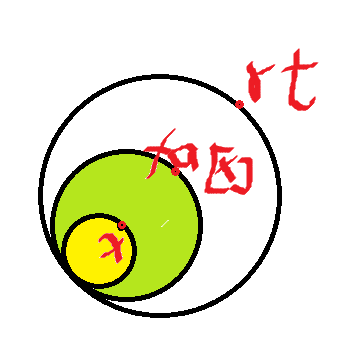
\(dum[fa[i]] - fum[i]\)是绿色部分的点\(y\)到\(fa[x]\)的\(d * dis(y, fa[x])\)值之和，\((sum[fa[i]] - sum[i]) * dist(fa[i], x)\)是绿色部分的点\(y\)的\(d\)值之和乘上\(dis(fa[x], x)\)，所以总体就是绿色部分的所有点到\(x\)的\(d * dis(y, x)\)值之和。

求\(dis(x, y)\)要用\(lca\)来求，求\(lca\)要用倍增的方法，这样时间复杂度低一点。

#include <bits/stdc++.h>

#define int long long

using namespace std;

inline long long read() {
    long long s = 0, f = 1; char ch;
    while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
    for(s = ch ^ 48;isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
    return s * f;
}

const int N = 5e5 + 5, inf = 1e9;
int n, m, rt, cnt, tot, root, totsize;
int f[N][23], fa[N], vst[N], de[N << 2], dep[N], dis[N], vis[N << 2], lg[N << 1], dfn[N], siz[N], link[N << 1], max_siz[N], head[N];
long long sum[N], dum[N], fum[N];
struct edge { int to, nxt, val; } e[N << 1];

void add(int x, int y, int z) {
    e[++cnt].nxt = head[x]; head[x] = cnt; e[cnt].to = y; e[cnt].val = z;
}

void get_root(int x, int Fa) {
    siz[x] = 1; max_siz[x] = 0;
    for(int i = head[x]; i ; i = e[i].nxt) {
        int y = e[i].to; if(y == Fa || vst[y]) continue;
        get_root(y, x);
        siz[x] += siz[y];
        max_siz[x] = max(max_siz[x], siz[y]);
    }   
    max_siz[x] = max(max_siz[x], totsize - siz[x]);
    if(max_siz[root] > max_siz[x]) root = x;
}

void build(int x, int Fa) {
    vst[x] = 1;
    for(int i = head[x]; i ; i = e[i].nxt) {
        int y = e[i].to; if(y == Fa || vst[y]) continue;
        max_siz[root = 0] = totsize = siz[y];
        get_root(y, x); fa[root] = x; link[i] = root;
        build(root, x);
    }
}

void dfs_pre(int x, int Fa) {
    dfn[x] = ++ tot; vis[tot] = x;
    dep[x] = dep[Fa] + 1; de[tot] = dep[x];
    for(int i = head[x]; i ; i = e[i].nxt) {
        int y = e[i].to; if(y == Fa) continue;
        dis[y] = dis[x] + e[i].val;
        dfs_pre(y, x);
        vis[++tot] = x; de[tot] = dep[x];
    }
}

void RMQ() {
    lg[0] = -1;
    for(int i = 1;i <= tot; i++) lg[i] = lg[i >> 1] + 1;
    for(int i = 1;i <= tot; i++) f[i][0] = i;
    for(int i = 1;i <= 21; i++) {
        if((1 << i) > tot) break;
        for(int j = 1;j <= tot; j++) {
            if(j + (1 << i) - 1 > tot) break;
            int a = f[j][i - 1], b = f[j + (1 << (i - 1))][i - 1];
            f[j][i] = de[a] < de[b] ? a : b;
        }
    } 
}

int LCA(int x, int y) {
    int l = dfn[x], r = dfn[y];
    if(l > r) swap(l, r);
    int k = lg[r - l + 1];
    int a = f[l][k], b = f[r - (1 << k) + 1][k];
    return de[a] < de[b] ? vis[a] : vis[b];
}

long long dist(int x, int y) {
    int lca = LCA(x, y);
    return dis[x] + dis[y] - 2 * dis[lca];
}

void change(int x, int _3k) {
    int y = x;
    while(x) {
        sum[x] += _3k;
        dum[x] += 1ll * _3k * dist(x, y);
        fum[x] += 1ll * _3k * dist(y, fa[x] ? fa[x] : x);
        x = fa[x];
    }
}

long long calc(int x) {
    long long res = dum[x];
    for(int i = x; fa[i]; i = fa[i]) 
        res += dum[fa[i]] - fum[i] + (sum[fa[i]] - sum[i]) * dist(fa[i], x);
    return res;
}

long long query() {
    int x = rt, y;
    long long res, tmp;
    while(1) {
        tmp = calc(x); y = x;
        for(int i = head[x]; i ; i = e[i].nxt) {
            int to = e[i].to; 
            res = calc(to);
            if(res < tmp) {
                tmp = res; y = link[i]; break;
            }
        }    
        if(x == y) break; x = y;
    }
    return tmp;
}

signed main() {

    // freopen("b.out","w",stdout);

    n = read(); m = read();
    for(int i = 1, x, y, z;i <= n - 1; i++) {
        x = read(); y = read(); z = read();
        add(x, y, z); add(y, x, z);
    }

    max_siz[root] = totsize = n; 
    get_root(1, 0);
    rt = root; build(root, 0);
    dfs_pre(1, 0); RMQ();

    for(int i = 1, x, y;i <= m; i++) {
        x = read(); y = read();
        change(x, y);
        printf("%lld\n", query());
    }

    return 0;
}

posted @ 2020-09-06 17:10 C锥阅读(142) 评论(0) 编辑收藏举报

刷新页面返回顶部

C锥