平衡树
P3369 【模板】普通平衡树
题目描述
您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:
- 插入 x 数
- 删除 x 数(若有多个相同的数,因只删除一个)
- 查询 x 数的排名(排名定义为比当前数小的数的个数 +1 )
- 查询排名为 x 的数
- 求 x 的前驱(前驱定义为小于 x,且最大的数)
- 求 x 的后继(后继定义为大于 x,且最小的数)
输入格式
第一行为 n,表示操作的个数,下面 n 行每行有两个数 opt和 x,opt表示操作的序号( 1≤opt≤6 )
输出格式
对于操作 3,4,5,6 每行输出一个数,表示对应答案
输入输出样例
输入 #1
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
输出 #1
106465
84185
492737
说明/提示
【数据范围】
对于 100% 的数据,1≤n≤\(10^5\),∣x∣≤\(10^7\)
\(Splay\)板子:
#include <bits/stdc++.h>
using namespace std;
inline long long read() {
long long s = 0, f = 1; char ch;
while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
for(s = ch ^ 48;isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
return s * f;
}
const int N = 1e5 + 5, inf = 1e9;
int n, tot, root;
struct node { int fa, val, cnt, siz, son[2]; } t[N]; //son[0/1]表示左右儿子
void up(int x) {
t[x].siz = t[x].cnt + t[t[x].son[0]].siz + t[t[x].son[1]].siz;
}
void rotate(int x) {
int y = t[x].fa, z = t[y].fa, k = t[y].son[1] == x;
if(z) t[z].son[t[z].son[1] == y] = x; t[x].fa = z;
t[y].son[k] = t[x].son[k ^ 1]; t[t[x].son[k ^ 1]].fa = y;
t[x].son[k ^ 1] = y; t[y].fa = x;
up(y); up(x);
}
void Splay(int x, int goal) {
if(goal == 0) root = x;
while(t[x].fa ^ goal) {
int y = t[x].fa, z = t[y].fa;
if(z ^ goal) (t[y].son[1] == x) ^ (t[z].son[1] == y) ? rotate(x) : rotate(y);
rotate(x);
}
}
void Insert(int x) {
int u = root, Fa = 0;
while(u && t[u].val ^ x) Fa = u, u = t[u].son[x > t[u].val];
if(u) t[u].cnt++;
else {
u = ++tot;
if(Fa) t[Fa].son[x > t[Fa].val] = u;
t[u].val = x; t[u].siz = 1; t[u].cnt = 1;
t[u].fa = Fa; t[u].son[0] = t[u].son[1] = 0;
}
Splay(u, 0);
}
void Find(int x) {
int u = root;
if(!u) return ;
while(t[u].son[x > t[u].val] && t[u].val ^ x) u = t[u].son[x > t[u].val];
Splay(u, 0);
}
int pre_nxt(int x, bool f) {
Find(x);
if(t[root].val < x && !f) return root;
if(t[root].val > x && f) return root;
int u = t[root].son[f];
while(t[u].son[f ^ 1]) u = t[u].son[f ^ 1];
return u;
}
void Delete(int x) {
int nxt = pre_nxt(x, 1), pre = pre_nxt(x, 0);
Splay(pre, 0); Splay(nxt, pre);
int u = t[nxt].son[0];
if(--t[u].cnt == 0) t[nxt].son[0] = 0, t[t[nxt].fa].siz--;
else Splay(u, 0);
}
int Kth(int k) {
int u = root;
while(1) {
if(t[t[u].son[0]].siz + t[u].cnt < k) {
k -= t[t[u].son[0]].siz + t[u].cnt;
u = t[u].son[1];
}
else if(t[t[u].son[0]].siz >= k) u = t[u].son[0];
else return t[u].val;
}
}
int main() {
n = read();
Insert(-inf); Insert(inf);
for(int i = 1, x, opt;i <= n; i++) {
opt = read(); x = read();
if(opt == 1) { Insert(x); }
else if(opt == 2) { Delete(x); }
else if(opt == 3) { Find(x); printf("%d\n", t[t[root].son[0]].siz); }
else if(opt == 4) { printf("%d\n", Kth(x + 1)); } //因为插入了-inf,所以要加1
else printf("%d\n", t[pre_nxt(x, opt == 6)].val);
}
return 0;
}
这一行:
if(z ^ goal) (t[y].son[1] == x) ^ (t[z].son[1] == y) ? rotate(x) : rotate(y);
这是\(Splay\)的双旋,目的是减小时间复杂度,因为减小了层数。
这一行:
int nxt = pre_nxt(x, 1), pre = pre_nxt(x, 0);
Splay(pre, 0); Splay(nxt, pre);
我们在删除一个节点\(x\)的时候,把\(x\)的前驱转到根,把\(x\)的后继转到根的下方,这时会发现:\(x\)就是后继的左儿子,并且\(x\)没有子树,这样删点就很舒服。
这一块:
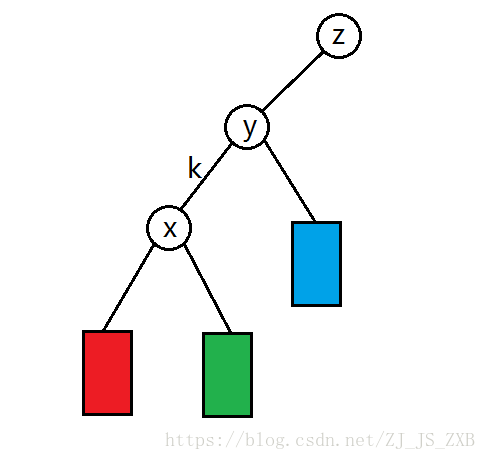
void rotate(int x) {
int y = t[x].fa, z = t[y].fa, k = t[y].son[1] == x;
if(z) t[z].son[t[z].son[1] == y] = x; t[x].fa = z;
t[y].son[k] = t[x].son[k ^ 1]; t[t[x].son[k ^ 1]].fa = y;
t[x].son[k ^ 1] = y; t[y].fa = x;
up(y); up(x);
}
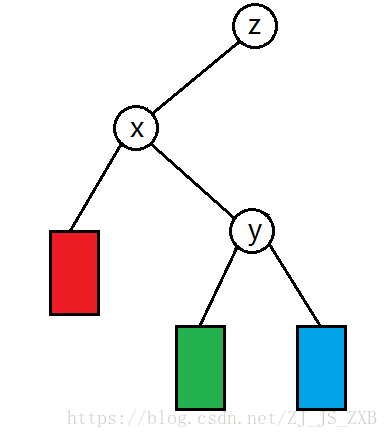
就是从左图旋转到右图。
其中\(t[x].son[k \ xor\ 1]\)就是图中绿色的的部分。
P1533 可怜的狗狗
就是平衡树板子题,涉及加点,删点,求第\(k\)大值。
对于每个询问排个序,这样加点或删点的时候移动的次数少一点,不会超时。
#include <bits/stdc++.h>
#define int long long
using namespace std;
inline long long read() {
long long s = 0, f = 1; char ch;
while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
for(s = ch ^ 48;isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
return s * f;
}
const int N = 1e6 + 5;
const long long inf = 1e13;
int n, m, tot, root;
int a[N], ans[N];
struct node { int fa, val, cnt, siz, son[2]; } t[N];
struct ques { int l, r, k, id; } q[N];
bool cmp(ques a, ques b) {
return a.l < b.l;
}
void up(int x) {
t[x].siz = t[x].cnt + t[t[x].son[0]].siz + t[t[x].son[1]].siz;
}
void rotate(int x) {
int y = t[x].fa, z = t[y].fa, k = t[y].son[1] == x;
if(z) t[z].son[t[z].son[1] == y] = x; t[x].fa = z;
t[y].son[k] = t[x].son[k ^ 1]; t[t[x].son[k ^ 1]].fa = y;
t[x].son[k ^ 1] = y; t[y].fa = x;
up(y); up(x);
}
void Splay(int x, int goal) {
if(goal == 0) root = x;
while(t[x].fa ^ goal) {
int y = t[x].fa, z = t[y].fa;
if(z ^ goal) (t[y].son[1] == x) ^ (t[z].son[1] == y) ? rotate(x) : rotate(y);
rotate(x);
}
}
void Insert(int x) {
int u = root, Fa = 0;
while(u && t[u].val ^ x) Fa = u, u = t[u].son[x > t[u].val];
if(u) t[u].cnt++;
else {
u = ++tot;
if(Fa) t[Fa].son[x > t[Fa].val] = u;
t[u].val = x; t[u].cnt = t[u].siz = 1;
t[u].fa = Fa; t[u].son[0] = t[u].son[1] = 0;
}
Splay(u, 0);
}
void Find(int x) {
int u = root;
if(!u) return ;
while(t[u].son[x > t[u].val] && t[u].val ^ x) u = t[u].son[x > t[u].val];
Splay(u, 0);
}
int pre_nxt(int x, bool f) {
Find(x);
if(t[root].val < x && !f) return root;
if(t[root].val > x && f) return root;
int u = t[root].son[f];
while(t[u].son[f ^ 1]) u = t[u].son[f ^ 1];
return u;
}
void Delete(int x) {
int nxt = pre_nxt(x, 1), pre = pre_nxt(x, 0);
Splay(pre, 0); Splay(nxt, pre);
int u = t[nxt].son[0];
if(--t[u].cnt == 0) t[nxt].son[0] = 0, t[t[nxt].fa].siz--;
else Splay(u, 0);
}
int Kth(int k) {
int u = root;
while(1)
if(t[t[u].son[0]].siz + t[u].cnt < k) {
k -= t[t[u].son[0]].siz + t[u].cnt;
u = t[u].son[1];
}
else if(t[t[u].son[0]].siz >= k) u = t[u].son[0];
else return t[u].val;
}
}
signed main() {
// freopen("a.in","r",stdin); freopen("a.out","w",stdout);
n = read(); m = read();
for(int i = 1;i <= n; i++) a[i] = read();
for(int i = 1;i <= m; i++) q[i].l = read(), q[i].r = read(), q[i].k = read(), q[i].id = i;
sort(q + 1, q + m + 1, cmp);
int x = 1, y = 0;
Insert(-inf); Insert(inf);
for(int i = 1;i <= m; i++) {
while(x > q[i].l) { x--; Insert(a[x]); }
while(y < q[i].r) { y++; Insert(a[y]); }
while(x < q[i].l) { Delete(a[x]); x++; }
while(y > q[i].r) { Delete(a[y]); y--; }
ans[q[i].id] = Kth(q[i].k + 1);
}
for(int i = 1;i <= m; i++) printf("%lld\n", ans[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号