主席树
可持久化线段树(主席树)
单点修改
1.单点修改时,我们考虑将包含该点\(k\)的线段树节点新建出一条链。(就像这样) 每次修改将创造出\(logn\)个新节点。
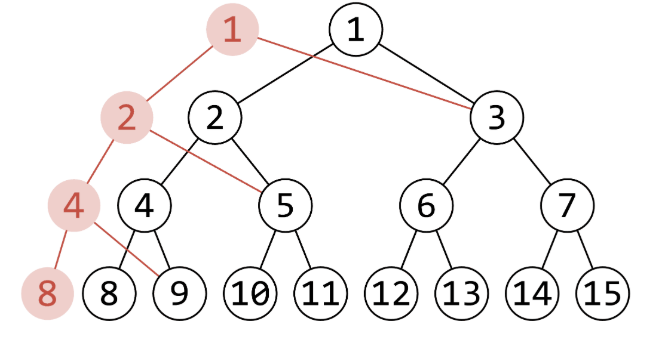
2.修改完的线段树不再是一颗完全二叉树,我们不能直接用层次编号,而是直接改为记录左右子节点的编号。大概的意思就是:不能用\(o << 1\)的方式去找o点的左儿子,而是要在结构体里新加一个东西,用\(t[o].lc\)去找他的左儿子。
struct Tree {
int lc, rc; //左右子树编号
int dat; //区间最大值
} t[N << 2];
int tot, root[N]; //可持久化线段树的总点数和每个根
int n, a[N];
void up(int p) {
t[p].dat = max(t[t[p].lc].dat, t[t[p].rc].dat);
}
int build(int l, int r) {
int p = tot++;
if(l == r) { t[p].dat = a[l]; return p; }
int mid = (l + r) >> 1;
t[p].lc = build(l, mid); t[p].rc = build(mid + 1, r);
up(p); return p;
}
root[0] = build(1, n); //调用入口
int insert(int now, int l, int r, int x, int val) {
int p = tot++;
t[p] = t[now];
if(l == r) { t[p].dat = val; return ; }
int mid = (l + r) >> 1;
if(x <= mid) t[p].lc = insert(t[now].lc, l, mid, x, val);
if(x > mid) t[p].rc = insert(t[now].rc, mid + 1, r, x, val);
up(p); return p;
}
root[i] = insert(root[i - 1], 1, n, x, val); //调用入口
cout << ask(root[v], 1, n, x);
然后这个题就可以做了:
区间第k小值
思想个上面那个差不多,只是用主席树的方法做。
P3834 【模板】可持久化线段树 2(主席树)(和poj2761一样,但是上面那个代码在poj过了,在luogu就过不了,不知道为啥,就很ex)
通过模拟数据来发现一些规律:
7
1 5 2 6 3 7 4
2 5 3

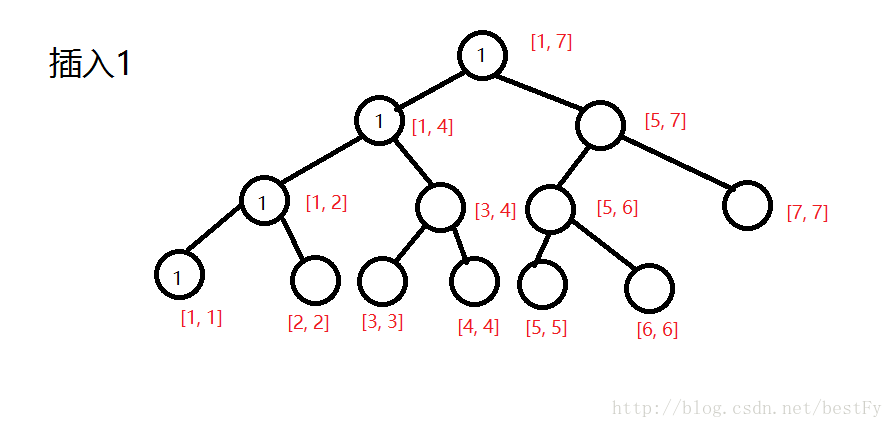
(第一棵树)
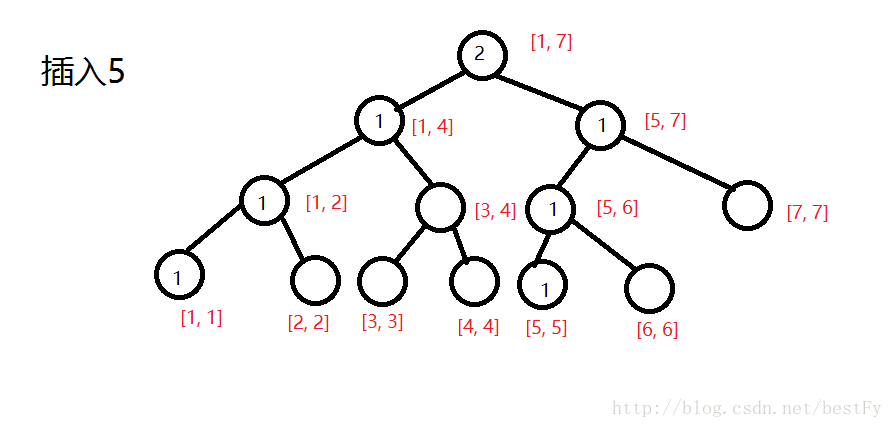
(第二棵树)
像这样一直插完。。。
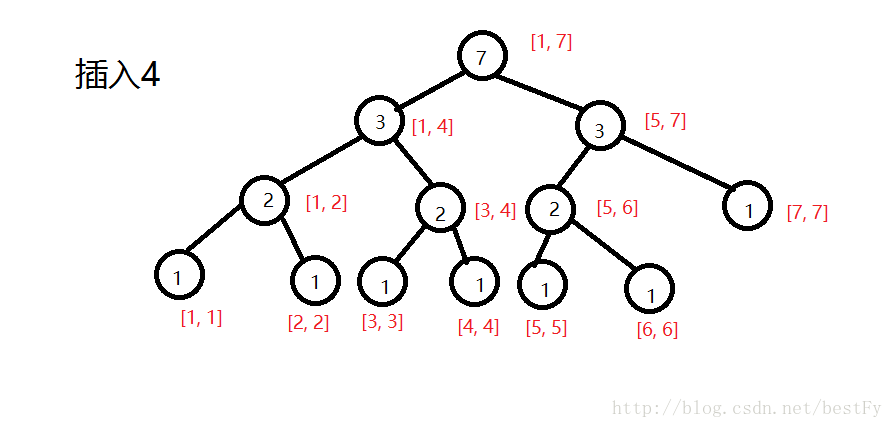
(第七棵树)
现在我们要询问区间[2, 5]第3大值,我们把第一棵树和第五棵树拿出来。
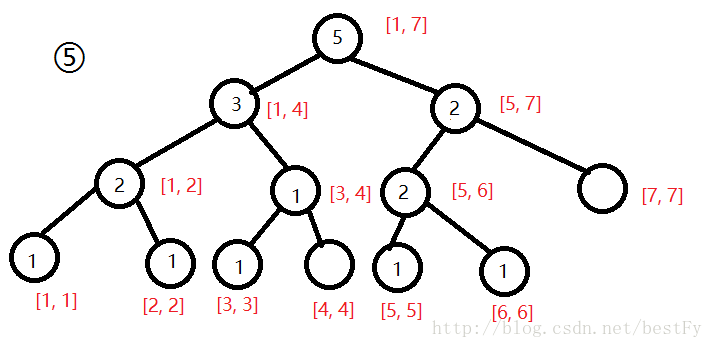
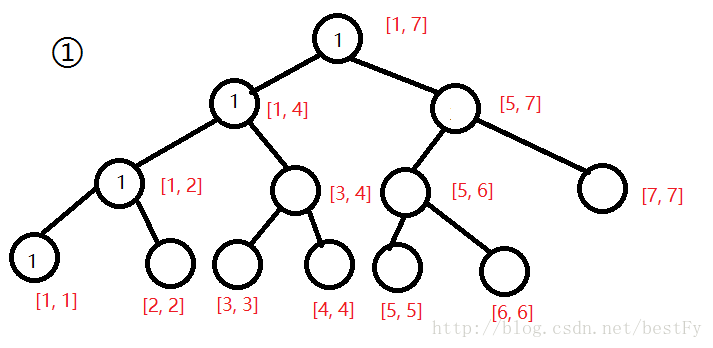
我们可以发现,对应节点的数字相减就可以得到1区间[2, 5]的数。(有点类似于前缀和)
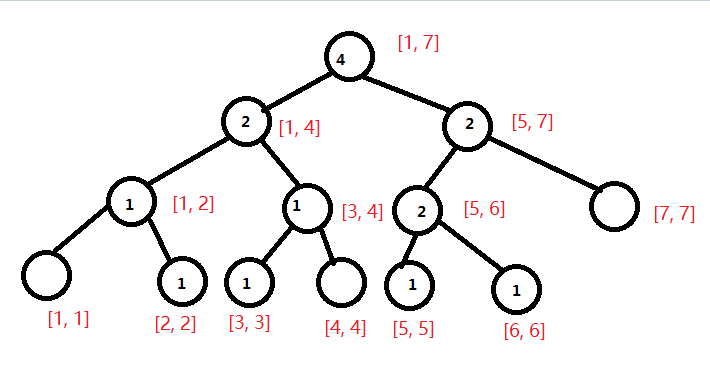
我们设\(u\)为编号小的树, \(v\)为编号大的树,设\(x = t[t[v.ls]].sum - t[t[u.ls]].sum\)。若\(k <= x\),则说明要找的数在左子树内;若\(k > x\),则说明要找的数在右子树内,于是我们去右子树找第\(k - x\)小的数。(和上面那个是不是很像)
这个主席树上是值域。
#include <iostream>
#include <cstdio>
#include <algorithm>
#define mid ((l + r) >> 1)
using namespace std;
inline int read() {
int s = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') { if(ch == '-') f = -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') { s = (s << 1) + (s << 3) + (ch ^ 48); ch = getchar(); }
return s * f;
}
const int N = 2e5 + 5;
int n, m, tot;
int a[N], b[N], root[N * 20];
struct tree { int lc, rc, sum; } t[N * 20];
int build(int l, int r) {
int p = ++tot;
if(l == r) { return p; }
t[p].lc = build(l, mid); t[p].rc = build(mid + 1, r);
return p; //一定要记得写,不然会RE
}
int change(int now, int l, int r, int k) {
int p = ++tot;
t[p].lc = t[now].lc; t[p].rc = t[now].rc; t[p].sum = t[now].sum + 1;
if(l == r) { return p; }
if(k <= mid) t[p].lc = change(t[now].lc, l, mid, k);
if(k > mid) t[p].rc = change(t[now].rc, mid + 1, r, k);
return p; //一定记得写
}
int query(int u, int v, int l, int r, int k) {
if(l == r) return l;
int x = t[t[v].lc].sum - t[t[u].lc].sum;
if(k <= x) return query(t[u].lc, t[v].lc, l, mid, k);
if(k > x) return query(t[u].rc, t[v].rc, mid + 1, r, k - x);
}
int main() {
n = read(); m = read();
for(int i = 1;i <= n; i++) b[i] = a[i] = read();
sort(b + 1, b + n + 1);
int cnt = unique(b + 1, b + n + 1) - b - 1;
root[0] = build(1, cnt); //这是那个空树,注意那个cnt,离散化之后序列长度就变为cnt了(把重复的数去掉了)
for(int i = 1;i <= n; i++) {
a[i] = lower_bound(b + 1, b + cnt + 1, a[i]) - b;
root[i] = change(root[i - 1], 1, cnt, a[i]);
}
for(int i = 1;i <= m; i++) {
int x = read(), y = read(), k = read();
printf("%d\n", b[query(root[x - 1], root[y], 1, cnt, k)]);
}
return 0;
}
水题
题目大意:给一个数列,每次询问一个区间内有没有一个数出现次数超过一半。没有的话输出0。
主席树水题。。。
我们现在要找一个区间[\(l\), \(r\)]的一个数出现次数大于\((r - l + 1)/2\)。令\(x = (r - l + 1)/2\), 我们像上面区间第\(k\)小值一样维护一个\(sum\)。如果一个节点的左儿子的\(sum * 2\)小于等于\(x\),那么这里面肯定没有符合要求的数。如果大于,这个数则在左子树内;右子树同理。
#include <iostream>
#include <cstdio>
#include <cctype>
#define mid ((l + r) >> 1)
using namespace std;
inline long long read() {
long long s = 0, f = 1; char ch;
while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
for(s = ch ^ 48;isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
return s * f;
}
const int N = 7e5 + 5;
int n, m, tot;
int root[N];
struct tree { int lc, rc, sum; } t[N * 20];
int build(int l, int r) {
int p = ++tot;
if(l == r) { return p; }
t[p].lc = build(l, mid); t[p].rc = build(mid + 1, r);
return p;
}
int insert(int res, int l, int r, int x) {
int p = ++tot;
t[p].lc = t[res].lc; t[p].rc = t[res].rc; t[p].sum = t[res].sum + 1;
if(l == r) { return p; }
if(x <= mid) t[p].lc = insert(t[res].lc, l, mid, x);
if(x > mid) t[p].rc = insert(t[res].rc, mid + 1, r, x);
return p;
}
int query(int L, int R, int l, int r, int x) {
if(l == r) { return l; }
int num1 = t[t[R].lc].sum - t[t[L].lc].sum;
int num2 = t[t[R].rc].sum - t[t[L].rc].sum;
if(num1 * 2 > x) return query(t[L].lc, t[R].lc, l, mid, x);
else if(num2 * 2 > x) return query(t[L].rc, t[R].rc, mid + 1, r, x);
else return 0;
}
int main() {
n = read(); m = read();
root[0] = build(1, n);
for(int i = 1, x;i <= n; i++) {
x = read(); root[i] = insert(root[i - 1], 1, n, x);
}
for(int i = 1, l, r;i <= m; i++) {
l = read(); r = read();
printf("%d\n", query(root[l - 1], root[r], 1, n, r - l + 1));
}
return 0;
}


