AC自动机

AC自动机

​ 给你\(n\)个模式串和1个文本串，问有多少个模式串在文本串里出现过。

​ 这就是AC自动机解决的问题，得用到Tire树和\(KMP\)的思想。

​ 如果我们枚举每一个模式串去和文本串匹配，那么复杂度是\(O(n^2)\)的。

​ 现在我们把每个模式串放到一颗Tire树上，根据\(KMP\)的思想搞一个\(fail\)数组，这个数组表示当前节点匹配不到了应该从哪里接着匹配，因为每次都从头开始匹配相当于还是\(n^2\)的。

​ 这个\(fail\)数组和\(KMP\)里的\(nxt\)数组都叫失配指针，可以看成是Tire树上一个字符连到另一个相同字符的东西。

​ 大佬的博客

​ 我们先建一颗Tire树：[\(she, shr, say, her\)]

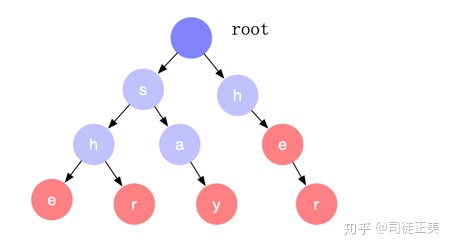
​ 连完\(fail\)数组是这样的：

​

​ 我们可以\(bfs\)求出\(fail\)数组，根的每个子节点都指向根，其它节点指向它父亲的\(fail\)的相同的子节点，如果没有相同的，指向根（0）就好了。

​ 还有一个注意的地方，找完“she”里面的“e”后，会找到“her”里面的“r"。（对应bfs里面的那个else）

#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>

using namespace std;

const int N = 1e6;
int n, cnt;
int ch[N][26], fail[N], val[N];
char a[N], b[N];

struct AC {
	void ins(char *a) {
		int len = strlen(a), p = 0;
		for(int i = 0;i < len; i++) {
			int num = a[i] - 'a';
			if(!ch[p][num]) ch[p][num] = ++cnt;
			p = ch[p][num];
		}
		val[p]++;
	}
	
	void make_fail() {
		queue <int> q;
		for(int i = 0;i < 26; i++) {
			if(ch[0][i]) fail[ch[0][i]] = 0, q.push(ch[0][i]); 
		}
		while(q.size()) {
			int x = q.front(); q.pop();
			for(int i = 0;i < 26; i++) {
				if(ch[x][i]) fail[ch[x][i]] = ch[fail[x]][i], q.push(ch[x][i]);
				else ch[x][i] = ch[fail[x]][i];
			}
		}
	}
	
	int match(char *b) {
		int len = strlen(b), p = 0, ans = 0;
		for(int i = 0;i < len; i++) {
			int num = b[i] - 'a';
			p = ch[p][num];
			for(int t = p;t && ~val[t]; t = fail[t]) ans += val[t], val[t] = -1; //~（-1） =  0
		}
		return ans;
	}
} cj;

int main() {

	scanf("%d", &n);
	for(int i = 1;i <= n; i++) { cin >> a; cj.ins(a); }
	cj.make_fail();
	cin >> b;
	printf("%d", cj.match(b));
	
	return 0;
}