结构体内的一些操作
结构体内的一些操作
重载
#include <bits/stdc++.h>
using namespace std;
struct test {
int a, b;
friend bool operator < (const test &x, const test &y) {
return x.a < y.a;
}
} x, y;
int main() {
cin >> x.a >> x.b>> y.a >> y.b;
if(x < y) cout << 1;
else cout << 0;
return 0;
}
加&:更快。相当于调用地址进行操作。如果不加&的话会非常慢,相当于把要操作的东西先复制了一遍。
加\(const\):保证要操作的东西不被改变。可以更快一点点。
加\(friend\):结构体中重载,后面如果有两个参数,必须加\(friend\)。如果在结构体外重载就不用加了。
返回类型:上面的就是返回的\(bool\)类型,因为是重载小于号,别的该返回啥返回啥。
关于堆的结构体重载:
struct node {
int x, y;
node() {};
node(int X, int Y) { x = X, y = Y; }
friend bool operator < (const node &a, const node &b) {
return a.x < b.x; //按x从大到小排序
// return a.x > b.x; //按x从小到大排序
}
} ;
priority_queue <node> q;
struct node {
int x, y;
node() {}
node(int X, int Y) { x = X, y = Y; }
friend bool operator > (const node &a, const node &b) {
return a.x > b.x; //按x从小到大排序
// return a.x < b.x //按x从大到小排序
}
}
priority_queue <node, vector<node>, greater<node> > q;
大根堆重载小于号,小根堆重载大于号
构造函数
#include <bits/stdc++.h>
using namespace std;
struct test {
int a, b;
char *ch[2], *t;
int e[233];
test(int c = 0, int d = 0, t = NULL) : a(c), b(d) { ch[0] = ch[1] = NULL; memset(e, 0, sizeof(e); }
};
int main() {
test x(1, 3), y;
cout << x.a << " " << x.b << "\n";
cout << y.a << " " << y.b << "\n";
return 0;
}
更简单的初始化,注意要赋值的东西对应好了就行。如果没有赋初值直接就是0。
保护(隐藏)
#include <bits/stdc++.h>
using namespace std;
struct Stack {
protected:
int a;
public:
void make() {
cout << ++a;
}
} cj;
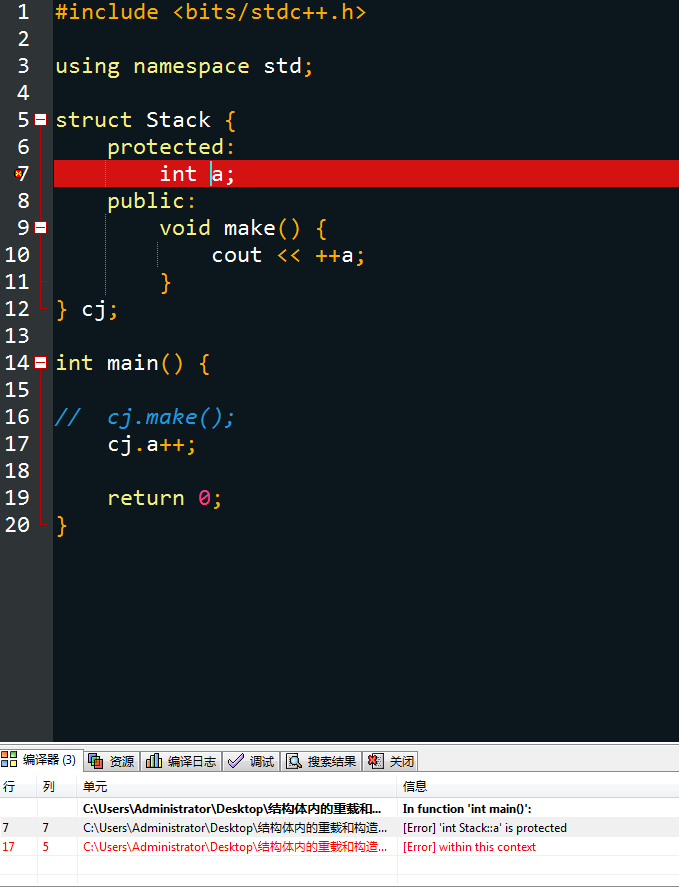
int main() {
cj.make();
// cj.a++;
return 0;
}
我们平常写的结构体内的所有东西都是在\(public\)中搞的,\(protected\)里搞的东西只能在这个结构体里用到,上面代码被注释的是错误写法,会报错:
最近在写树剖,用到了这个,可以结合代码理解一下怎么用:
#include <iostream>
#include <cstdio>
#include <cctype>
#define ls(o) (o << 1)
#define rs(o) (o << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
inline long long read() {
long long s = 0, f = 1; char ch;
while(!isdigit(ch = getchar())) (ch == '-') && (f = -f);
for(s = ch ^ 48; isdigit(ch = getchar()); s = (s << 1) + (s << 3) + (ch ^ 48));
return s * f;
}
const int N = 5e5 + 5;
int n, m, mod, cnt, tot, root;
int a[N], A[N], fa[N], dep[N], hav[N], siz[N], top[N], dfn[N], head[N];
struct edge { int nxt, to; } e[N << 1];
void add(int x, int y) {
e[++cnt].nxt = head[x]; head[x] = cnt; e[cnt].to = y;
}
struct Tree {
protected:
struct tree { int sum, tag; } t[N << 2];
void up(int o) {
t[o].sum = (t[ls(o)].sum + t[rs(o)].sum) % mod;
}
void modify(int o, int l, int r, int k) {
(t[o].tag += k) %= mod; t[o].sum = (t[o].sum + 1ll * (r - l + 1) * k % mod) % mod;
}
void down(int o, int l, int r) {
modify(ls(o), l, mid, t[o].tag); modify(rs(o), mid + 1, r, t[o].tag); t[o].tag = 0;
}
void build(int o, int l, int r) {
if(l == r) { t[o].sum = A[l] % mod; return; }
build(ls(o), l, mid); build(rs(o), mid + 1, r);
up(o);
}
void change(int o, int l, int r, int x, int y, int k) {
if(x <= l && y >= r) { modify(o, l, r, k); return ;}
if(t[o].tag) down(o, l, r);
if(x <= mid) change(ls(o), l, mid, x, y, k);
if(y > mid) change(rs(o), mid + 1, r, x, y, k);
up(o);
}
int query(int o, int l, int r, int x, int y) {
if(x <= l && y >= r) { return t[o].sum; }
if(t[o].tag) down(o, l, r);
int res = 0;
if(x <= mid) res = (res + query(ls(o), l, mid, x, y)) % mod;
if(y > mid) res = (res + query(rs(o), mid + 1, r, x, y)) % mod;
return res;
}
public:
void build() { build(1, 1, n); }
void change(int x, int y, int k) { change(1, 1, n, x, y, k); }
int query(int x, int y) { return query(1, 1, n, x, y); }
} cj;
void get_tree(int x, int Fa) {
siz[x] = 1; dep[x] = dep[fa[x] = Fa] + 1;
for(int i = head[x]; i; i = e[i].nxt) {
int y = e[i].to; if(y == Fa) continue;
get_tree(y, x); siz[x] += siz[y];
if(siz[y] > siz[hav[x]]) hav[x] = y;
}
}
void get_top(int x, int topic) {
top[x] = topic; A[dfn[x] = ++tot] = a[x];
if(hav[x]) get_top(hav[x], topic);
for(int i = head[x]; i; i = e[i].nxt) {
int y = e[i].to;
if(y == fa[x] || y == hav[x]) continue;
get_top(y, y);
}
}
void changepath(int x, int y, int k) {
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
int fx = top[x]; cj.change(dfn[fx], dfn[x], k);
x = fa[fx];
}
if(dep[y] > dep[x]) swap(x, y);
cj.change(dfn[y], dfn[x], k);
}
int querypath(int x, int y) {
int res = 0;
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
int fx = top[x]; res = (res + cj.query(dfn[fx], dfn[x])) % mod;
x = fa[fx];
}
if(dep[y] > dep[x]) swap(x, y);
res = (res + cj.query(dfn[y], dfn[x])) % mod;
return res;
}
int main() {
n = read(); m = read(); root = read(); mod = read();
for(int i = 1;i <= n; i++) a[i] = read();
for(int i = 1, x, y;i <= n - 1; i++) x = read(), y = read(), add(x, y), add(y, x);
get_tree(root, 0);
get_top(root, root);
cj.build();
for(int i = 1, opt, x, y, z;i <= m; i++) {
opt = read();
if(opt == 1) {
x = read(); y = read(); z = read(); changepath(x, y, z % mod);
}
else if(opt == 2) {
x = read(); y = read(); printf("%d\n", querypath(x, y));
}
else if(opt == 3) {
x = read(); z = read(); cj.change(dfn[x], dfn[x] + siz[x] - 1, z % mod);
}
else {
x = read(); printf("%d\n", cj.query(dfn[x], dfn[x] + siz[x] - 1));
}
}
return 0;
}
封装
像上面那个树剖的代码,我在结构体里不仅定义了一些变量,而且搞了一些函数。
struct test {
int AoLiGei(int a, int b) {
return a + b;
}
} cj;
int main() {
int x, y;
cin >>x, y;
cout << cj.AoLiGei(x, y);
}
这个小程序就会输出\(x + y\)。其实就跟调用结构体里面的变量是一样的,只是\(.\)(点)后面的变量名改成了函数名。
这么写的好处是可以让你的代码更加清晰,就像上面树剖的代码,我线段树的东西都放在一个结构体里,你写的时候就很清晰。而且如果相似的函数很多,这么写也挺好的。


