线段树的一些经典操作
线段树
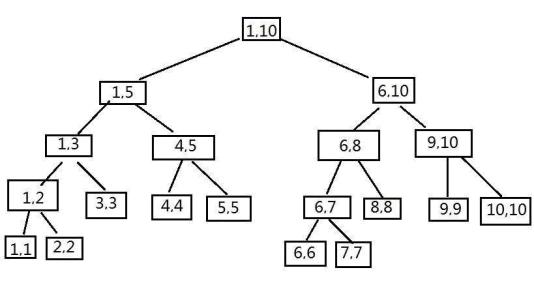
(线段树就长这样)
一些性质
1.左儿子是父节点编号的二倍，右儿子是父节点编号的二倍加一。
#define ls(o) （o << 1）
#define rs(o) （o << 1 | 1）
2.线段树数组长度不能小于4N。
3.对于一个区间[\(l\), \(r\)]， 它的左儿子是[\(l\), \(mid\)]， 右儿子是[\(mid\) + 1, \(r\)]。
#define mid （(l + r) >> 1）
4.线段树去掉最后一层一定是完全二叉树，深度为\(logn\)。
建树
void up(int o) {
t[o].dat = t[ls(o)].dat + t[rs(o)].dat; //从下往上走的时候子节点更新父节点
}
void build(int o, int l ,int r) {
if(l == r) {t[o].dat = read(); return ;} //递归到叶子节点
build(ls(o), l, mid), build(rs(o), mid + 1, r); //递归左右子树
up(o);
}
build(1, 1, n); //调用入口
单点修改
void change(int o, int l ,int r, int x, int k) { //将x位置的值改为k
if(l == r) { t[o].dat = k; return ;} //找到x位置，修改
if(x <= mid) change(ls(o), l, mid, x, k);
if(x > mid) change(rs(o), mid + 1, r, x, k);
up(o); //一定记得要更新
}
区间查询
int ask(int o, int l, int r, int x, int y) {
if(x <= l && r <= y) return t[o].dat; //当覆盖了一个完整的区间，直接返回这个区间的值，这就是线段树为啥很快
int res = 0;
if(x <= mid) res += ask(ls(o), l, mid, x, y); //一定注意是x <= mid, 不是l <= mid，我在这里死了好几次了
if(y > mid) res += ask(rs(o), mid + 1, r, x, y);
return res;
}
区间修改
void modify(int o, int l, int r, int k) {
tag[o] += k; t[o].dat += (r - l + 1) * k;
}
void down(int o, int l, int r) {
if(tag[o] != 0) modify(ls(o), l, mid, tag[o]), modify(rs(o), mid + 1，r, tag[o]), tag[o] = 0;
}
void change(int o, int l, int r, int x, int y, int k) {
if(x <= l && r <= y) { return modify(o, l, r, k); }
down(o, l, r);
if(x <= mid) change(ls(o), l, mid, x, y, k);
if(y > mid) changr(rs(o), mid + 1, r, x, y, k);
up(o); //记得更新
}
区间修改的时候我们引入懒标记\(tag\)数组。
我们修改区间[\(l\), \(r\)]时，以该节点为根的子树所有点都要修改，复杂度为\(O(n)\)。
类似区间查询，我们如果发现[\(l\), \(r\)]包含在修改区间中，我们直接给这个节点打上\(tag\)懒标记，然后返回，等到后续的指令里需要从该节点向下递归时，我们直接下传标记，使两个子节点具有标记，然后该节点标记清零。
使用懒标记后复杂度降为\(O(logn)\)。
带修改最大子段和
void up(int o) {
t[o].dat = t[ls(o)].dat + t[rs(o)].dat;
t[o].l = max(t[ls(o)].l, t[ls(o)].dat + t[rs(o)].l);
t[o].r = max(t[rs(o)].r, t[rs(o)].dat + t[ls(o)].r);
t[o].s = max(max(t[ls(o)].s, t[rs(o)].s), t[ls(o)].r + t[rs(o)].l);
}
这道题求带修改最大子段和。
我们考虑线段树多维护一点东西，分别是紧靠左端的最大子段和，紧靠右端的最大子段和，最大子段和。
维护紧靠左端最大子段和：将 左子树紧靠左端的最大子段和 与 左子树的所有点的和+右子树紧靠左端的最大子段和 取\(max\)。（维护紧靠右端最大子段和也同理）
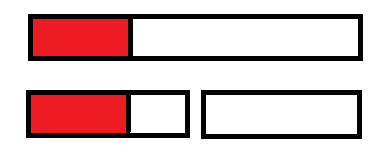
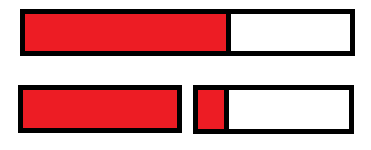
维护最大子段和：将 左子树最大子段和 ， 右子树最大子段和 与 左子树紧靠右端子段和+右子树紧靠左端子段和 取\(max\)。
区间染色
poj 2777
题目大意：有一个长度为\(L\)的色板，可均匀地分为\(L\)个小格。
有两种操作：\(C\) \(l\) \(r\) \(x\) 表示把区间[\(l\), \(r\)]染为颜色\(x\) (\(x\) <= 30)；
\(P\) \(l\) \(r\) 表示询问区间[\(l\), \(r\)]有几种颜色。
这道题的不同点在于它新的颜色会覆盖掉原来的颜色，但是我们发现它的颜色个数很少，我们可以用二进制压缩来做，每一个线段树上存一个二进制数，第\(i-1\)位为1表示这个区间具有颜色\(i\)。
在询问颜色个数时，我们可以将每个区间的二进制数用 | 来合并。
#include <iostream>
#include <cstdio>
#define ls(o) (o << 1)
#define rs(o) (o << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
inline int read() {
int s = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') { if(ch == '-') f = -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') { s = (s << 1) + (s << 3) + (ch ^ 48); ch = getchar(); }
return s * f;
}
const int N = 1e6 + 5;
int n, T, m;
struct tree { int d, tag; } t[N << 2];
void up(int o) {
t[o].d = t[ls(o)].d | t[rs(o)].d;
}
void modify(int o, int l, int r, int k) {
t[o].tag = 1; t[o].d = k; //这里是将父节点的颜色都给了子节点，有人可能会想父节点的颜色个数不一定就等于子节点的颜色个数呀。这个函数实际上是在tag不为 0的时候执行的，也就数说该父节点一定是一种颜色，所以他的子节点也是和父亲节点一样的颜色。
}
void down(int o, int l, int r) {
if(t[o].tag != 0) modify(ls(o), l, mid, t[o].d), modify(rs(o), mid + 1, r, t[o].d), t[o].tag = 0;
}
void build(int o, int l, int r) {
if(l == r) { t[o].tag = t[o].d = 1; return ;}
build(ls(o), l, mid); build(rs(o), mid + 1, r);
up(o);
}
void change(int o, int l, int r, int x, int y, int val) {
if(x > r || y < l) return ;
if(x <= l && y >= r) {
t[o].tag = 1; t[o].d = (1 << (val - 1)); return ; //记得减一
}
down(o, l, r);
if(y <= mid) change(ls(o), l, mid, x, y, val);
else if(x > mid) change(rs(o), mid + 1, r, x, y, val);
else {
change(ls(o), l, mid, x, y, val);
change(rs(o), mid + 1, r, x, y, val);
}
up(o);
}
int query(int o, int l, int r, int x, int y) {
if(x <= l && y >= r) { return t[o].d; }
down(o, l, r);
if(y <= mid) return query(ls(o), l, mid, x, y);
else if(x > mid) return query(rs(o), mid + 1, r, x, y);
else {
int a = query(ls(o), l, mid, x, y), b = query(rs(o), mid + 1, r, x, y);
return a | b;
}
}
int main() {
n = read(); T = read(); m = read();
build(1, 1, n);
for(int i = 1;i <= m; i++) {
char ch; cin >> ch;
if(ch == 'C') {
int x = read(), y = read(), val = read();
if(x > y) swap(x, y); //这里一定要记得写
change(1, 1, n, x, y, val);
}
else {
int x = read(), y = read();
if(x > y) swap(x, y); //记得写
int ans = query(1, 1, n, x, y);
int num = 0;
while(ans) {
if(ans & 1) num++;
ans >>= 1; //和快速幂那个差不多，检查哪一位是一，然后记录答案
}
printf("%d\n", num);
}
}
return 0;
}
区间第k小值
poj 2761
题目大意：给定一个长度为\(n\)的序列，有\(m\)条询问，询问区间[\(l\), \(r\)]的第\(k\)小值为多少，没有一个区间完全包含另一个区间，只可能会交叉。
这道题的做法挺多的，有平衡树，主席树。线段树也可以做，相对简单一点。
''没有一个区间完全包含另一个区间，只可能会交叉。''这句话的意思是一个区间的起点只对应一个终点， 或者说一个区间的终点只对应一个起点。
首先离散化。然后我们考虑线段树多维护一点东西，\(t[o].small\)表示在当前有序线段树内小于\(mid\)的个数，也可以说是左子树的大小。
对于每一个询问，我们可以把它们都离线下来，按左端点排序，使用两个指针\(x\), \(y\)，不断移向新的区间，每加入一个数或丢出一个数就更改线段树来维护\(small\)。找当前询问第\(k\)小值时，递归线段树，如果\(k <= t[o].small\)，说明这个第\(k\)小值在\(o\)的左子树内；如果\(k > t[o].small\)，说明这个第\(k\)小值在\(o\)的右子树内，那就找右子树的第\(k - t[o].small\)小值。
#include <iostream>
#include <cstdio>
#include <algorithm>
#define ls(o) (o << 1)
#define rs(o) (o << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
inline int read() {
int s = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') { if(ch == '-') f = -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') { s = (s << 1) + (s << 3) + (ch ^ 48); ch = getchar(); }
return s * f;
}
const int N = 1e5 + 10;
int n, m, cnt;
int a[N], b[N], ans[N * 5];
struct tree { int small; } t[N << 2];
struct ask { int l, r, k, id; } q[N * 5];
int cmp(ask a, ask b) { return a.l < b.l; }
void change(int o, int l, int r, int x, int flag) {
if(l == r) return ;
if(x <= mid) t[o].small += flag, change(ls(o), l, mid, x, flag);
else change(rs(o), mid + 1, r, x, flag);
}
int query(int o, int l, int r, int k) {
if(l == r) return l;
if(k <= t[o].small) return query(ls(o), l, mid, k);
else return query(rs(o), mid + 1, r, k - t[o].small);
}
int main() {
n = read(); m = read();
for(int i = 1;i <= n; i++) b[i] = a[i] = read();
sort(b + 1, b + n + 1);
int cnt = unique(b + 1, b + n + 1) - b - 1;
for(int i = 1;i <= n; i++) {
a[i] = lower_bound(b + 1, b + cnt + 1, a[i]) - b;
} //离散化
for(int i = 1;i <= m; i++) {
q[i].l = read(); q[i].r = read(); q[i].k = read(); q[i].id = i;
}
sort(q + 1, q + m + 1, cmp);
int x = q[1].l, y = x;
for(int i = 1;i <= m; i++) {
while(x < y && x < q[i].l) {
change(1, 1, n, a[x], -1); x++; //丢出一个数
}
if(y < q[i].l) y = q[i].l;
while(y <= q[i].r) {
change(1, 1, n, a[y], 1); y++; //加入一个数
}
ans[q[i].id] = b[query(1, 1, n, q[i].k)];
}
for(int i = 1;i <= m; i++) printf("%d\n", ans[i]);
return 0;
}
求LIS
怎么用线段树求带修改最长上升子序列。
题目大意：有\(n\)（位置从1到\(n\)）个楼房，开始时高度都为零。有\(m\)个操作，每次输入\(x\), \(y\),表示把位置为\(x\)的楼房的高度改为\(y\)。每次操作后都要输出一个数，表示当前修改完后从0位置能看见的楼房个数。
很显然，这道题让你求的是最长上升子序列。但不是找楼房高度的最长上升子序列，因为在后面的楼房虽然可能会比前面的高，但不一定会看见，比如：
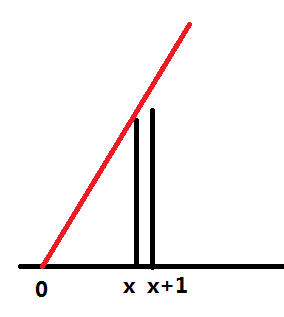（看不见吧）
我们发现，只要把高度转化为斜率就好了，是0位置连楼房顶端的直线的斜率，问题变成了求斜率的最长上升子序列。
现在考虑线段树维护什么东西。维护一个区间内最长上升子序列，维护一个斜率最大值。斜率最大值比较好转移，直接对左右子树的斜率最大值取\(max\)就好了。那怎么转移区间内最长上升子序列呢？
首先，一个区间[\(l\), \(r\)]内的最长上升子序列一定包括左端点\(l\)，对于叶子节点它的区间内最长上升子序列是1。
设一个区间的最长上升子序列为\(len\)，这个区间的\(len\)一定大于等于左儿子的\(len\)，因为它一定包含左儿子的左端点，也就是它的左端点。对于它的右儿子，如果它右儿子的左儿子的斜率最大值比它的左儿子的斜率最大值小（或者等于）（有点绕，好好想想），那么就没有它的右儿子的左儿子的事了，直接找右儿子的右儿子，方法和这个相同；如果它右儿子的左儿子的斜率最大值比它的左儿子的斜率最大值大，说明这个区间内对答案有贡献，用同样的方法找右儿子的左儿子，然后加上\(len\)（它的右儿子） - \(len\)（它的右儿子的左儿子）。（这里看不懂的可以画个图理解一下或结合代码理解一下)
#include <iostream>
#include <cstdio>
#define ls(o) (o << 1)
#define rs(o) (o << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
const int N = 1e5 + 10;
int n, m;
double a[N];
struct tree { double mk; int len; } t[N << 2];
inline int read() {
int s = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') { if(ch == '-') f = -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') { s = (s << 1) + (s << 3) + (ch ^ 48); ch = getchar(); }
return s * f;
}
void up1(int o) { t[o].mk = max(t[ls(o)].mk, t[rs(o)].mk); }
int up2(int o, int l, int r, double lm) { //传进来的lm一定要开double，要不你都不知道你怎么死的
if(t[o].mk <= lm) { return 0; } //如果这个区间的斜率最大值小于等于lm，说明这个区间都不可能对答案有贡献，直接返回0
if(a[l] > lm) { return t[o].len; } //如果这个区间内的左端点的斜率比lm大，说明这个区间的len可以直接加到答案里面
if(l == r) { return a[l] > lm; } //找到了叶子节点，如果这个点的斜率大于lm，说明这个点对答案有1的贡献
if(t[ls(o)].mk <= lm) return up2(rs(o), mid + 1, r, lm); //这里就是上面那一段很绕的话
else return up2(ls(o), l, mid, lm) + t[o].len - t[ls(o)].len;
}
void change(int o, int l, int r, int x, int h) {
if(l == r) { t[o].mk = (double)h / x; t[o].len = 1; return ; }
if(x <= mid) change(ls(o), l, mid, x, h);
if(x > mid) change(rs(o), mid + 1, r, x, h);
up1(o);
t[o].len = t[ls(o)].len + up2(rs(o), mid + 1, r, t[ls(o)].mk);
}
int main() {
n = read(); m = read();
for(int i = 1;i <= m; i++) {
int x = read(), y = read();
a[x] = (double)y / x;
change(1, 1, n, x, y);
printf("%d\n", t[1].len);
}
return 0;
}
区间面积并
题目大意：给你\(n\)个矩形，让你求这\(n\)个矩形覆盖的面积是多少，重叠部分只算一次。
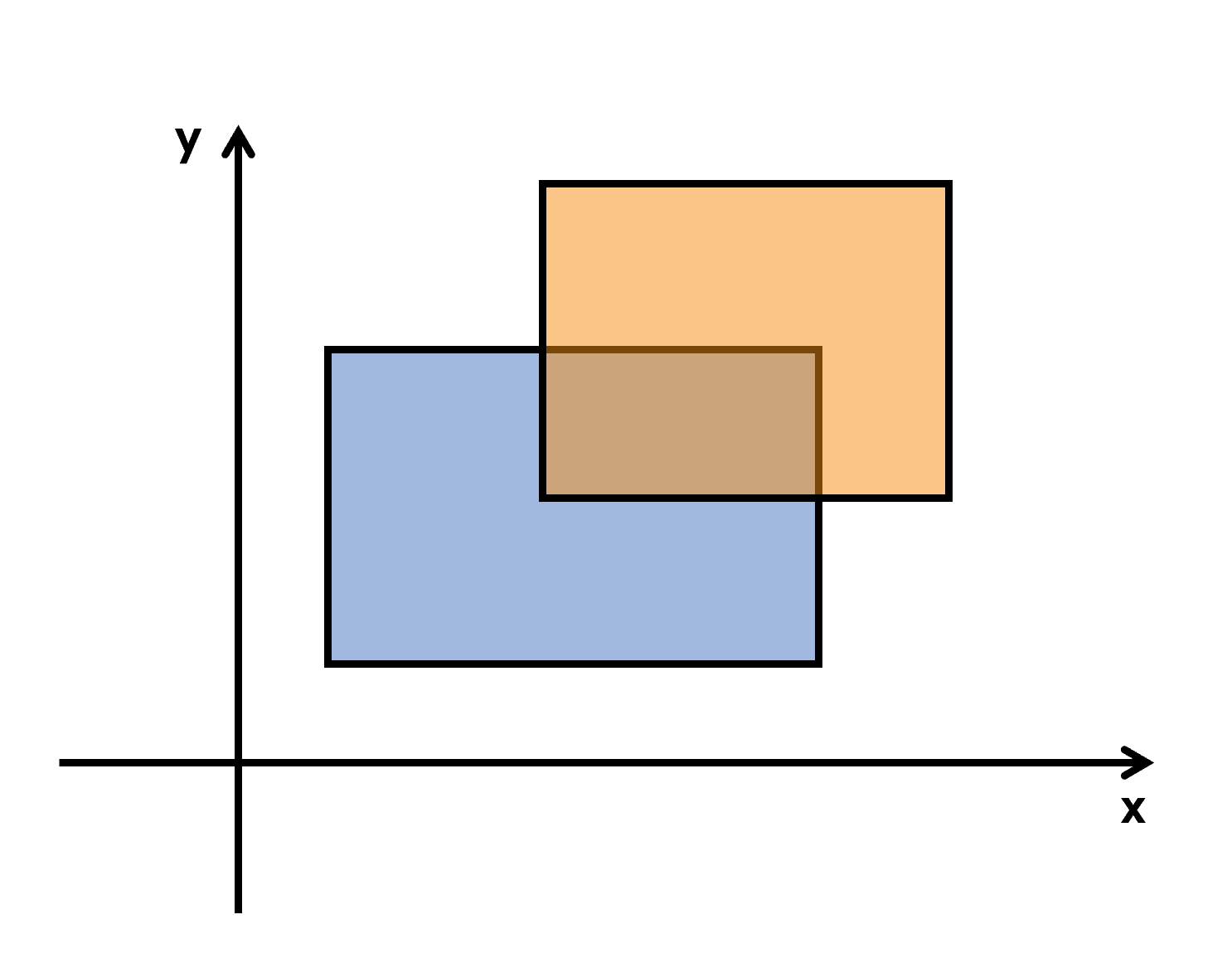
我们从下往上扫描一遍，只要碰到矩形的上底或下底就记录一下，将扫描到的线记为一个四元组\((x1, x2, h, flag)\)，分别表示这一条线的左端点，右端点，纵坐标，是下底还是上底（下底为1，上底为-1）。（个数是\(2n\)个）
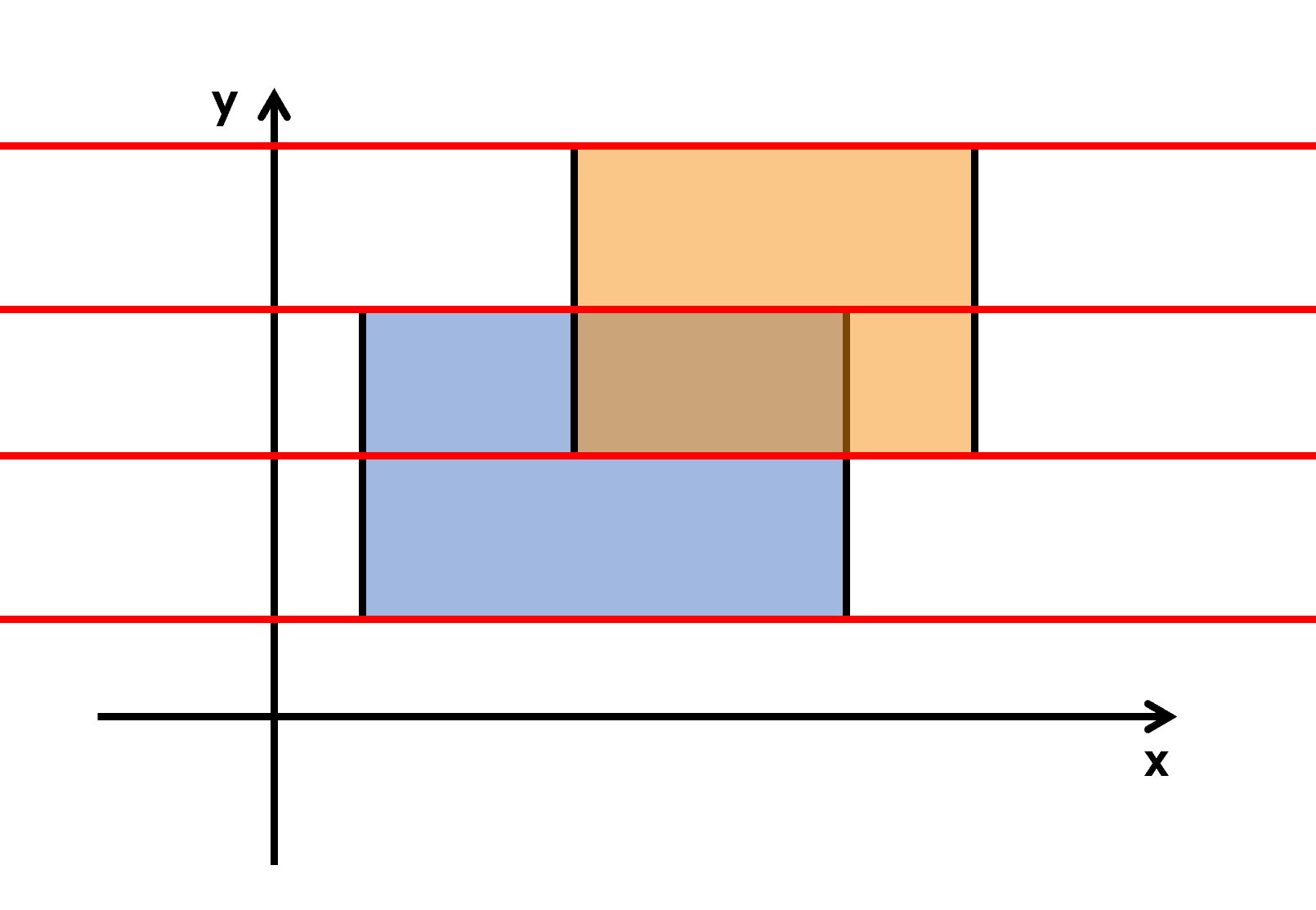
首先肯定要离散化，我们设\(X[x]\)表示\(x\)被离散化后的值。
然后我们考虑线段树怎么用，让线段树维护一个长度\((len)\)和权值\((sum)\)，权值表示该节点自身被覆盖的次数，长度表示该节点被矩形覆盖的长度。当从下往上扫，扫到第一条线的时候，1， 2节点会被更新；扫到第二条线的时候，1， 2， 3， 5， 6节点就会被更新。只要这个节点的权值大于0，那么它的就可以被算到面积里。
\(S = \displaystyle \sum_{i = 1}^{n - 1} t[1].len * (h[i + 1] - h[i])\)。
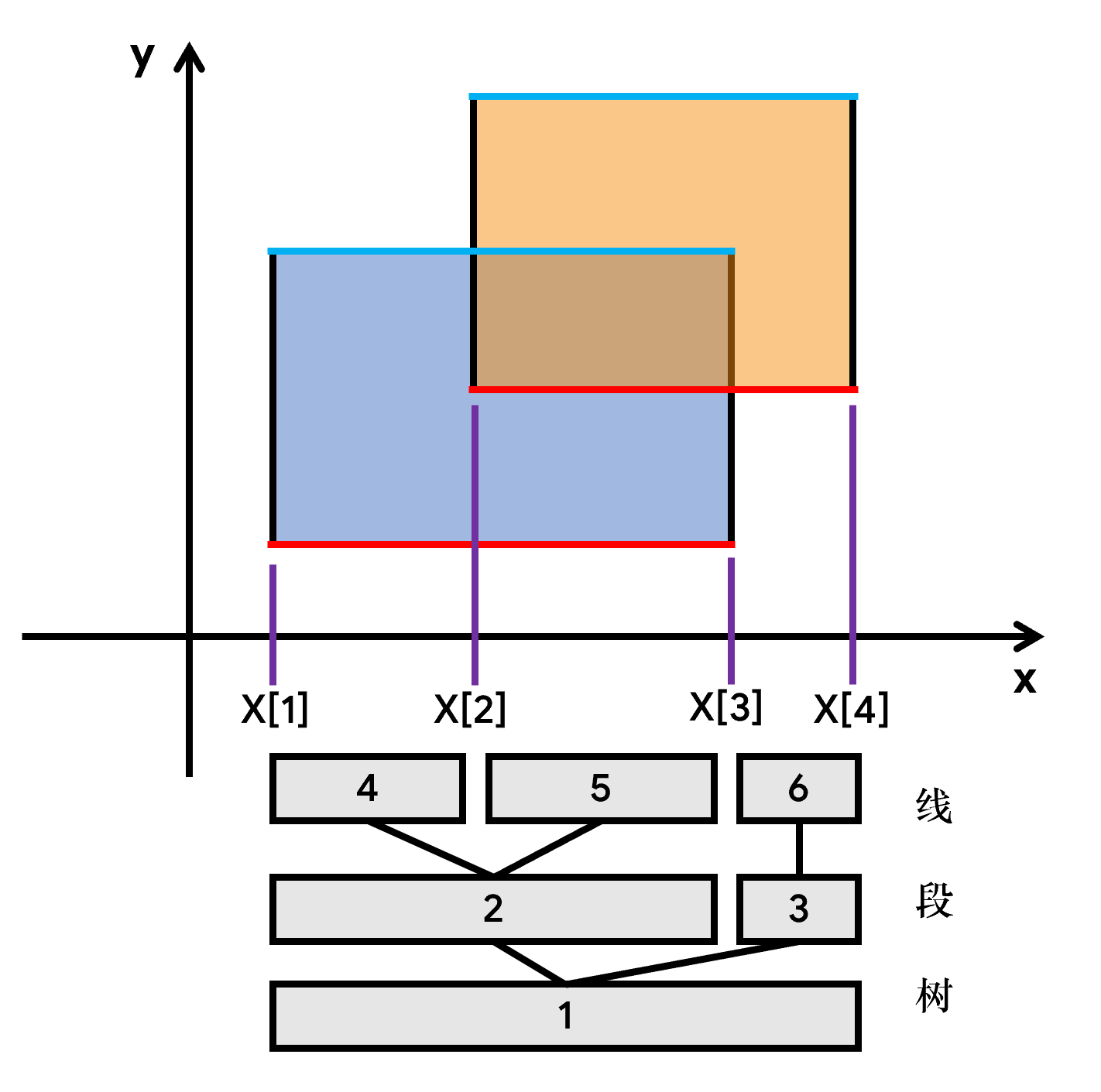
那么怎么更新\(len\)呢？如果\(t[o].sum != 0\)，说明这个节点被矩形覆盖（完全覆盖）了，\(t[o].len = x_r - x_l\)就可以了；如果这个节点没有被矩形完全覆盖，直接把它的左右儿子的\(len\)加起来就好了。
得注意的是线段树上节点2管到的区间是[1, 2]，节点3管到的区间是[3, 3]。为啥没有4，因为4个点只有三段。
#include <iostream>
#include <cstdio>
#include <algorithm>
#define ls(o) (o << 1)
#define rs(o) (o << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
inline long long read() {
long long s = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') { if(ch == '-') f = -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') { s = (s << 1) + (s << 3) + (ch ^ 48); ch = getchar(); }
return s * f;
}
const int N = 1e6 + 5; //题目数据给的1e5，但是开1e6才能过去，要不就二十分，并且是WA不是RE，就很离谱
int n, maxn, X[N << 1], raw[N << 1];
long long ans;
struct Line {
int l, r, h, flag;
friend bool operator < (Line a, Line b) { return a.h < b.h; }
} line[N << 1];
struct tree { int len, sum; } t[N << 3];
void up(int o, int l, int r) {
if(t[o].sum != 0) t[o].len = raw[r + 1] - raw[l]; //这里注意加一
else t[o].len = t[ls(o)].len + t[rs(o)].len;
}
void change(int o, int l, int r, int x, int y, int k) {
if(x <= l && y >= r) { t[o].sum += k; up(o, l, r); return ;}
if(x <= mid) change(ls(o), l, mid, x, y, k);
if(y > mid) change(rs(o), mid + 1, r, x, y, k);
up(o, l, r);
}
int main() {
n = read();
for(int i = 1;i <= n; i++) {
int x, y, z, u;
x = read(); y = read(); z = read(); u = read();
line[i * 2 - 1] = (Line) {x, z, y, 1};
line[i * 2] = (Line) {x, z, u, -1};
X[i * 2 - 1] = x; X[i * 2] = z;
}
n <<= 1;
sort(X + 1, X + n + 1);
int cnt = unique(X + 1, X + n + 1) - X - 1;
for(int i = 1;i <= n; i++) {
int pos1 = lower_bound(X + 1, X + cnt + 1, line[i].r) - X;
int pos2 = lower_bound(X + 1, X + cnt + 1, line[i].l) - X;
raw[pos1] = line[i].r; raw[pos2] = line[i].l; //原坐标
line[i].r = pos1, line[i].l = pos2; //离散化后，是上面的X数组
}
sort(line + 1, line + n + 1);
for(int i = 1;i < n; i++) { //最后一条线肯定不用算
change(1, 1, n, line[i].l, line[i].r - 1, line[i].flag); //这里为啥要减一呢？因为线段树的两个节点不可能重合，比如[1, 5], [6, 9],而 不能写成[1, 5][5, 9]，但图中是重合的，所以要减一。
ans += t[1].len * 1ll * (line[i + 1].h - line[i].h);
}
printf("%lld", ans);
return 0;
}
区间排序
题目大意：给你一个1到\(n\)的排列，有\(m\)次操作。“\(0 \ l \ r\)”表示将区间[\(l\), \(r\)]的数升序排列；“\(1 \ l \ r\)”表示将区间[\(l\), \(r\)]的数降序排列。最后询问位置\(q\)上的数是多少。
我们可以二分位置\(q\)上的数，设为\(mid\)。将序列里小于\(mid\)的数看成0，将大于等于\(mid\)的数看成1。对于每次排序，我们直接排序0和1就好。说是排序，其实就是把1放前面（后面），把0放后面（前面）。比如现在是升序排列区间[\(l\), \(r\)]，我们只要知道了此区间1的个数，那么就可以将[\(l\), \(r - cnt + 1\) ]全部附盖为0，将[\(r - cnt\)， \(r\)]全部覆盖为1，于是问题就转化成了区间修改，区间查询，单点查询。
所以线段树维护一个区间1的个数就好啦。
还有一个注意的地方，将区间全部覆盖为0和全部覆盖为1的\(tag\)值不同，注意区分就好了。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define ls(o) (o << 1)
#define rs(o) (o << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
inline int read() {
int s = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') { if(ch == '-') f = -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') { s = (s << 1) + (s << 3) + (ch ^ 48); ch = getchar(); }
return s * f;
}
const int N = 1e5 + 5;
int n, m, p, ans;
int a[N], b[N];
struct tree {
int tag, one;
tree():one(0) {}
} t[N << 2];
struct que { int opt, x, y; } q[N];
void up(int o) {
t[o].one = t[ls(o)].one + t[rs(o)].one;
}
void modify(int o, int l, int r, int k) {
t[o].tag = k;
if(k == 1) t[o].one = r - l + 1; else t[o].one = 0;
}
void down(int o, int l, int r) {
if(t[o].tag == 0) return ;
if(t[o].tag == 1) { modify(ls(o), l, mid, 1), modify(rs(o), mid + 1, r, 1); }
if(t[o].tag == -1) { modify(ls(o), l, mid, -1), modify(rs(o), mid + 1, r, -1); }
t[o].tag = 0;
}
void build(int o, int l, int r, int x) {
if(l == r) { t[o].one = a[l] >= x; t[o].tag = 0; return ; }
build(ls(o), l, mid, x); build(rs(o), mid + 1, r, x);
up(o); t[o].tag = 0;
}
void change1(int o, int l, int r, int x, int y, int val) {
if(x <= l && y >= r) { t[o].one = val * (r - l + 1); t[o].tag = val ? 1 : -1; return ; }
if(x > r || y < l) return ;
down(o, l, r);
if(x <= mid) change1(ls(o), l, mid, x, y, val);
if(y > mid) change1(rs(o), mid + 1, r, x, y, val);
up(o);
}
int query1(int o, int l, int r, int x, int y) {
if(x <= l && y >= r) { return t[o].one; }
if(x > r || y < l) return 0;
down(o, l, r);
int res = 0;
if(x <= mid) res += query1(ls(o), l, mid, x, y);
if(y > mid) res += query1(rs(o), mid + 1, r, x, y);
return res;
}
int query2(int o, int l, int r, int p) {
if(l == r && r == p) {return t[o].one; }
down(o, l, r);
if(p <= mid) return query2(ls(o), l, mid, p);
if(p > mid) return query2(rs(o), mid + 1, r, p);
}
int judge(int Mid) {
build(1, 1, n, Mid);
for(int i = 1;i <= m; i++) {
int cnt = query1(1, 1, n, q[i].x, q[i].y);
if(q[i].opt == 1) {
change1(1, 1, n, q[i].x, q[i].x + cnt - 1, 1);
change1(1, 1, n, q[i].x + cnt, q[i].y, 0);
}
else {
change1(1, 1, n, q[i].y - cnt + 1, q[i].y, 1);
change1(1, 1, n, q[i].x, q[i].y - cnt, 0);
}
}
return query2(1, 1, n, p);
}
int main() {
freopen("seq.in","r",stdin);
freopen("seq.out","w",stdout);
n = read(); m = read();
for(int i = 1;i <= n; i++) a[i] = read();
for(int i = 1;i <= m; i++) { q[i].opt = read(); q[i].x = read(); q[i].y = read(); }
p = read();
int ll = 1, rr = n;
while(ll <= rr) {
int midd = (ll + rr) >> 1;
if(judge(midd)) ans = midd, ll = midd + 1;
else rr = midd - 1;
}
printf("%d", ans);
fclose(stdin); fclose(stdout);
return 0;
}
区间开方
题目大意：\(n\)个数，\(m\)个操作：“0，l，r”表示将区间[\(l\), \(r\)]的每个数开方，“1，l，r”表示询问区间[\(l\),\(r\)]的数的总和。
对于一个\(10^{12}\)大小的数，开方6次就可以变为1（自己可以用计算器试一试）。我们用线段树写的话，维护一个区间和，再维护一个开方次数就好了。对于一个开方过6次的区间，我们直接返回区间和就好了；如果开方次数小于等于6次，那就递归到叶子节点，暴力开方就好。
我们发现，如果一个区间的和小于等于区间长度，那么这个区间一定被开方了6次以上，那么我们就可以少维护一个开方次数，直接维护一个区间和就行了，递归的时候我们如果发现\(t[o].sum <= r - l + 1\)，直接返回，用不着接着向下递归了（具体看代码吧）。
#include <iostream>
#include <cstdio>
#include <cmath>
#define ls(o) (o << 1)
#define rs(o) (o << 1 | 1)
#define mid ((l + r) >> 1)
using namespace std;
inline long long read() {
long long s = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') { if(ch == '-') f = -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') { s = (s << 1) + (s << 3) + (ch ^ 48); ch = getchar(); }
return s * f;
}
const int N = 5e5 + 5;
long long n, m;
struct tree { long long sum; } t[N << 2];
void up(int o) {
t[o].sum = t[ls(o)].sum + t[rs(o)].sum;
}
void build(int o, int l, int r) {
if(l == r) { t[o].sum = read(); return ;}
build(ls(o), l, mid); build(rs(o), mid + 1, r);
up(o);
}
void change(int o, int l, int r, int x, int y) {
if(l == r) { t[o].sum = sqrt(t[o].sum); return ; }
if(t[o].sum <= r - l + 1) { return ; }
if(x <= mid) change(ls(o), l, mid, x, y);
if(y > mid) change(rs(o), mid + 1, r, x, y);
up(o);
}
long long query(int o, int l, int r, int x, int y) {
if(x <= l && y >= r) { return t[o].sum; }
long long res = 0;
if(x <= mid) res += query(ls(o), l, mid, x, y);
if(y > mid) res += query(rs(o), mid + 1, r, x, y);
return res;
}
int main() {
n = read();
build(1, 1, n);
m = read();
for(int i = 1, opt, x, y;i <= m; i++) {
opt = read(); x = read(); y = read();
if(x > y) swap(x, y); //一定记得判断一下
if(opt == 0) {
change(1, 1, n, x, y);
}
else {
printf("%lld\n", query(1, 1, n, x, y));
}
}
return 0;
}
摇花手飞走（233 )
