除法运算的汇编优化(用乘法和右移来代替)
今天在反编译一段程序时发现了一些奇怪的代码,耗费了一天的时间终于弄懂了这段算法
| push ebp |
| mov ebp,esp |
| mov ecx,ss:[ebp+0x8] |
| mov eax,0x88888889 |
| mul ecx |
| shr edx,0x5 |
| mov eax,edx |
| shl eax,0x4 |
| sub eax,edx |
| add eax,eax |
| add eax,eax |
| sub ecx,eax |
| push esi |
| mov esi,edx |
| mov eax,0x88888889 |
| mul esi |
| push edi |
| mov edi,ss:[ebp+0xC] |
| mov ds:[edi],ecx |
| mov ecx,edx |
| shr ecx,0x5 |
| mov edx,ecx |
| shl edx,0x4 |
| sub edx,ecx |
| add edx,edx |
| add edx,edx |
| sub esi,edx |
| mov eax,0xAAAAAAAB |
| mul ecx |
| mov ds:[edi+0x4],esi |
| mov esi,edx |
| shr esi,0x4 |
| lea eax,ds:[esi+esi*2] |
| add eax,eax |
| add eax,eax |
| add eax,eax |
| sub ecx,eax |
| mov eax,0x8421085 |
| mul esi |
| mov ds:[edi+0x8],ecx |
| mov ecx,esi |
| sub ecx,edx |
| shr ecx,0x1 |
| add ecx,edx |
| shr ecx,0x4 |
| mov edx,ecx |
| shl edx,0x5 |
| sub edx,ecx |
| sub esi,edx |
| mov eax,0xAAAAAAAB |
| mul ecx |
| shr edx,0x3 |
| lea eax,ds:[edx+edx*2] |
| add eax,eax |
| add eax,eax |
| sub ecx,eax |
| inc ecx |
| add edx,0x7D0 |
| inc esi |
| push edi |
| mov ds:[edi+0xC],esi |
| mov ds:[edi+0x10],ecx |
| mov ds:[edi+0x14],edx |
| call <sub_45630C0> |
| add esp,0x4 |
| cmp ds:[edi+0x4],0x0 |
| mov eax,edi |
| jge 0x4563293 |
| mov ds:[edi+0x4],0x0 |
| pop edi |
| pop esi |
| pop ebp |
| ret |
将除法转换为乘法的MagicNumber:
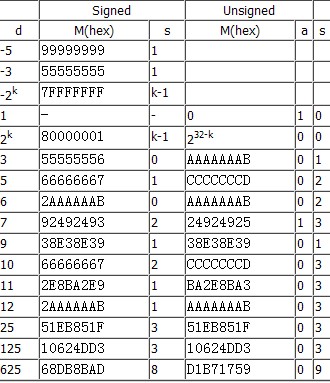
除以60 0x88888889
MagicNumber=2^33/被除数+1
所以被除数等于2^33/(MagicNumber-1)
不过除以有2的倍数因子的数时候,后边会跟shr edx,xx一类的指令或者mov xxx,edx
shr xxx,xx
比如除以72
会先除以9,再把商右移3次
除数的算法,例如开头的一段汇编代码:
mov eax,0x88888889
mul ecx
shr edx,0x5
除数=(2^(32+5))/(0x88888889-1)=60.000000013969838622484784252589
所以: 除数=60
乘法也会优化
31乘以某个数能不能写成这个数乘以2的次幂 再减去这个数。
用数学语言表达一下就是:
设这个数为x
31*x=x*2^n-x
这个等式是否存在,如果存在,求n的值
那我们计算一下,
31=2^n -1
得2^n=32
得n=5
也就是说存在那么一个n使得,31乘以某个数的结果等于这个数乘以2的n次幂再减去一个数。
所以,一个乘法运算,最后就转化成了一个速度较快的移位运算了。
以下资料参考网页:
https://www.jianshu.com/p/c2ecadbb7b19
0x01 除法优化浅析
最近花了点时间去逆向一些小程序,遇到“(R0 * 0xAAAAAAAB) >> 32”这样的运算时,一时看不出何意。后来经过搜索,才知道这是编译器对除法做的优化(因为除法指令比较耗时)。在这里做个小笔记。
对于除法操作,如果除数是2的整数次方,那直接右移就可以了。比如:R0/4可以用R0>>2代替。如果除数不是2的整数次方,那如何优化呢?简单写一下原理:

结合示例来看:
void test(unsigned int a)
{
LOG("unsigned int a / 3 = %d", a / 3);
}test函数很简单,看一下反汇编代码(主要关心其中的a/3):
LDR R2, =0xAAAAAAAB UMULL.W R2, R3, R0, R2 LSRS R1, R3, #1
R0即test函数的参数a,最后a/3的计算结果保存在R1中。
首先,R0和R2做无符号数乘法(UMULL),结果的高32位保存到R3,低32位保存到R2。R2的值后续并没有用到,相当于舍弃了,即只保留R0*R2的高32位,也就是相当于整个乘法运算的结果右移了32位。所以前2行代码即:(R0 * R2) >> 32。
第3行代码,又把R3逻辑右移了1位,所以这3行代码合起来就是:(R0 * R2) >> 33。而R2的值是0xAAAAAAAB,所以最终结果就是:(R0 * 0xAAAAAAAB) >> 33。也就是编译器将a/3优化成了(a * 0xAAAAAAAB) >> 33。那么这个结果,与上面提到的除法优化原理(a/b = (a*c) >> n,其中c=(2^n)/b)吻合吗?
从“(a * 0xAAAAAAAB) >> 33”可知,编译器选择的n值为33,那么c=(2 ^ 33)/b。这里除数b为3,所以c=(2^33)/3=2863311530.67,向上取整为2863311531,换成16进制,即:0xAAAAAAAB。所以,这里编译器所做的优化与上面提到的优化原理正好吻合。
刚才有一个c从2863311530.67向上取整为2863311531的操作,那么c的值就有一个0.33的误差。那为什么这个误差不会影响到最后的计算结果呢?这个是可以进行推理证明的,可以参考:https://www.cnblogs.com/shines77/p/4189074.html
0x02 由汇编反推除法
再来看一个例子,巩固一下。假设有以下3行反汇编代码,现在来反推回高级代码。
LDR R2, =0xCCCCCCCD
UMULL.W R2, R3, R0, R2
LSRS R1, R3, #2
3行代码合起来即:(R0 * 0xCCCCCCCD) >> 34。
除法优化原理:a/b = (a*c) >> n,其中c=(2^n)/b。
由(R0 * 0xCCCCCCCD) >> 34,可知n=34,c=0xCCCCCCCD。根据c=(2^ n)/b,可知b=(2^ n)/c=(2^34)/0xCCCCCCCD=4.99999999971,即b=5(因为c值有一个很小的,不影响除法运算结果的误差,所以这里得到的值近似5)。所以,上述3行汇编代码对应的高级代码即:R0/5。与实际的源码正好对应的上:
void test(int a) {
LOG("int a / 5 = %d", a / 5);
}
再回头看一下刚开始提到的“R0 * 0xAAAAAAAB >> 32”,这个对应的高级代码应该是什么?
除法优化原理:a/b = (a*c) >> n,其中c=(2^n)/b。
由“(R0 * 0xAAAAAAAB) >> 32”,可知n=32,c=0xAAAAAAAB。根据c=(2^ n)/b,可知b=(2^ n)/c=(2^32)/0xAAAAAAAB=1.49999999983,即b=1.5。所以“(R0 * 0xAAAAAAAB) >> 32”即R0/1.5。不过,这里提到的除法优化是针对整数常量来说的,所以实际就是R0/(3/2),即R0*2/3。
0x03 有符号数的除法优化
现在把test函数简单修改一下:
void test(int a) {
LOG("int a / 3 = %d", a / 3);
}
原先参数类型是unsigned int,现在参数类型是int。看一下a/3对应的反汇编代码:
LDR R2, =0x55555556
MOV R1, R0
SMULL.W R2, R3, R0, R2
SUB.W R1, R3, R1,ASR#31
这4行代码合起来就是:(R0 * 0x55555556) >> 32 – (R0 >> 31),其中R0 >> 31是算数右移。先忽略后面的减法,只关心“(R0*0x55555556)>>32”。
除法优化原理:a/b = (a*c) >> n,其中c=(2^n)/b。
由“(R0 * 0x55555556) >> 32”,可知n=32,c=0x55555556。根据c=(2^ n)/b,可知b=(2^ n)/c=(2^32)/0x55555556=2.9999999986,即b=3。所以“(R0 * 0x55555556) >> 32”即R0/3。这么一看,貌似后面的“– (R0 >> 31)”是多余的。其实不然,简单分析一下。
参数类型是int,“R0 >> 31”就是取符号位(算数右移)。那么有两种情况:
1)R0是正数,那么R0 >> 31结果为0,减法相当于什么也没做。
除法优化原理还是:a/b = (a*c) >> n,其中c=(2^n)/b。
2)R0是负数,那么R0 >> 31结果为0xFFFFFFFF,即-1,减-1相当于加1。
除法优化原理变成:a/b =( (a*c) >> n) + 1,其中c=(2^n)/b。
为什么被除数为负数时,后面要加1呢?因为“(a*c) >> n”是向下取整的结果。加1是为了向0取整,而c/c++语言对于整数除法的规定正是向0取整。
关于除法优化,还有很多更复杂的情况,以及一系列的理论推导。限于时间,我就先了解到这。对于简单的情况,能根据反汇编代码,反推回优化之前的除法操作了。
作者:十八垧
链接:https://www.jianshu.com/p/c2ecadbb7b19
来源:简书


