分组密码体制【密码学笔记】

分组密码的基本概念

​ 分组密码在加密过程中不是将明文按字符逐位加密，而是首先要将待加密的明文进行分组，每组的长度相同，然后对每组明文分别加密得到密文。加密和解密过程采用相同的密钥，称为对称密码体制。

​ 例如将明文分为\(m\)块：\(P_{0},P_{1},P_2,…,P_{m-1}\)，每个块在密钥作用下执行相同的变换，生成\(m\)个密文块：\(C_0,C_1,C_2,…,C_{m-1}\)，每块的大小可以是任意长度，但通常是每块的大小大于等于64位（块大小为1比特位时，分组密码就变为序列密码）。

如下图所示是通信双方最常用的分组密码基本通信模型。

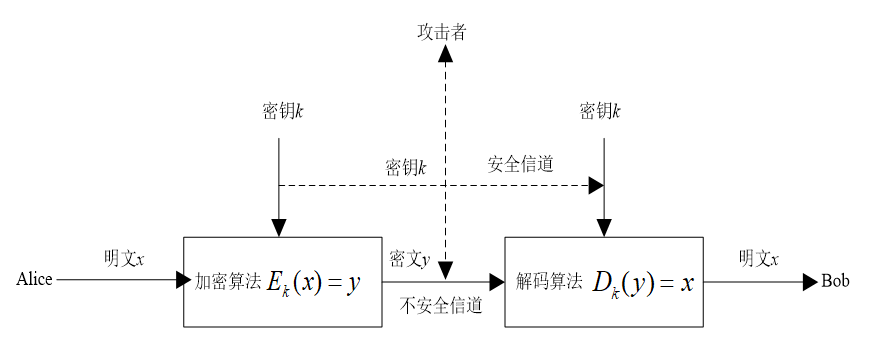
​ 一个分组密码系统(Block Cipher System，简称BCS）可以用一个五元组来表示：\(BCS=\{P,C,K,E,D\}\)。其中，P(plaintext)、C(ciphertext)、K(key)、E(encryption)、D(decode)分别代表明文空间、密文空间、密钥空间、加密算法、解密算法。

设\(X=\{x_0,x_1,…,x_{n-2},x_{n-1}\}\)为一组长度为 \(n\) 的明文块，在密钥\(K=\{k_0,k_1,…,k_{t-1}\}\)的加密作用下得到密文块\(Y=\{y_0,y_1,…,y_{m-2},y_{m-1}\}\)，其中\(x_i,y_j,k_r∈GF(2)\)，且

\[0≤i≤n-1,0≤j≤m-1,0≤r≤t-1 \]

　　若\(n=m\)，明文块长度等于密文块长度，称之为无数据扩展和压缩的分组密码；
　　若\(n>m\)，明文块长度大于密文块长度，称之为有数据压缩的分组密码；
　　若\(n<m\)，明文块长度小于密文块长度，称之为有数据扩展的分组密码。

为了保证分组密码的安全强度，设计分组密码时应遵循如下的基本原则：

• 分组长度足够长，防止明文穷举攻击，例如DES（Data Encryption Standard）、IDEA（International Data Encryption Algorithm）等分组密码算法，分组块大小为\(64\ bit\)，在生日攻击下用\(2^{32}\)组密文，破解成功的概率为\(0.5\)，同时要求\(2^{32}×64\ bit=2^{15}\ MB\)大小的存储空间，故在目前环境下采用穷举攻击DES、IDEA等密码算法是不可能的（\(2^{15}MB\)，也即是\(32G\)内存，这个是做得到的。做不到的是穷举 \(2^{32}\) 组密文。）；而AES明文分组为\(128\ bit\)，同样在生日攻击下用\(2^{64}\)组密文，破解成功的概率为\(0.5\)，同时要求存储空间大小为\(2^{64}×128\ bit=2^{48}\ MB\)，所以采用穷举攻击AES算法在计算上就更不可行。

• 密钥量足够大，同时需要尽可能消除弱密钥的使用，防止密钥穷举攻击，但是由于对称密码体制存在密钥管理问题，密钥也不能过大。

• 密钥变换足够复杂，能抵抗各种已知攻击，如差分攻击、线性攻击、边信道攻击等，即使得攻击者除了穷举攻击外找不到其它有效的攻击方法。

• 加密和解密的运算简单，易于软硬件高速实现。

• 数据扩展足够小，一般无数据扩展。

• 差错传播尽可能小，加密或解密某明文或密文分组出错，对后续密文解密的影响也尽可能小。

分组密码的原理

20世纪40年代末，香农在遵循柯克霍夫原则（ 即使密码系统的任何细节已为人悉知，只要密匙（key）未泄漏，它也应是安全的。 ）前提下，提出了设计密码系统的两个基本方法——扩散和混淆，目的是抗击攻击者对密码系统的统计分析。

• 扩散：将明文的统计特性（每个字母出现的频度）散布到密文中去，实现方式是使得明文的每一位影响密文中多位的值，等价于密文中每一位均受明文中多位的影响。在分组密码中，对数据重复执行某个置换，再对这一置换作用于一函数，可获得扩散。
• 混淆：使密文和密钥之间的统计关系变得尽可能复杂，使得攻击者无法得到密文和密钥之间的统计，从而攻击者无法得到密钥。

代替—置换网络结构（S-P结构）

　　1949年，香农在他的论文中提出了一种乘积密码，实现混淆和扩散。乘积密码通常伴随一系列置换与代替操作，常见的乘积密码是迭代密码。许多分组密码重复一个或几个步骤：代替然后换位，之后再代替，再换位等，并且每个步骤的过程都由密钥来控制。目前的大多数分组密码同时使用代替-置换网络以达到混淆和扩散的目标。 代替-置换网络是由多重代替变换(S)和置换变换（P）构成，如下图所示，S代替操作起到混淆的作用，P置换操作起到扩散的作用。

## Feistel密码结构

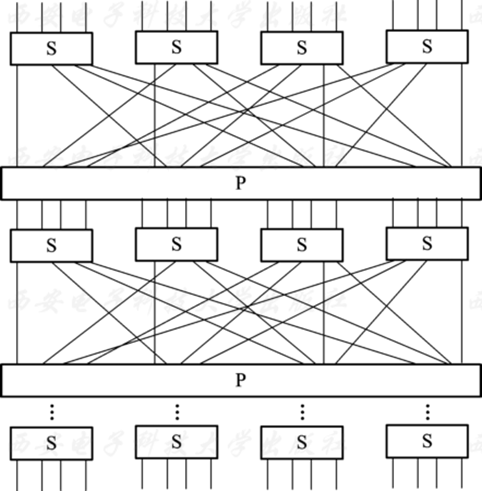
　　最典型的乘积密码是在1973年由Feistel提出的，整个处理过程包括多轮的代替和置换操作，主密钥可生产一个子密钥集\(k_i\)，每轮使用一个子密钥。在每轮中，明文被分为左右两部分,分别记为\(L_0\)和\(R_0\)，两部分分别进行交换，其中一个部分与子密钥混合，进行相应变换（可以把F视为一个函数），其中 \(\oplus\) 是异或运算。

在进行完 \(n\) 轮迭代之后，左右两半合并在一起再产生密文。示意图如下

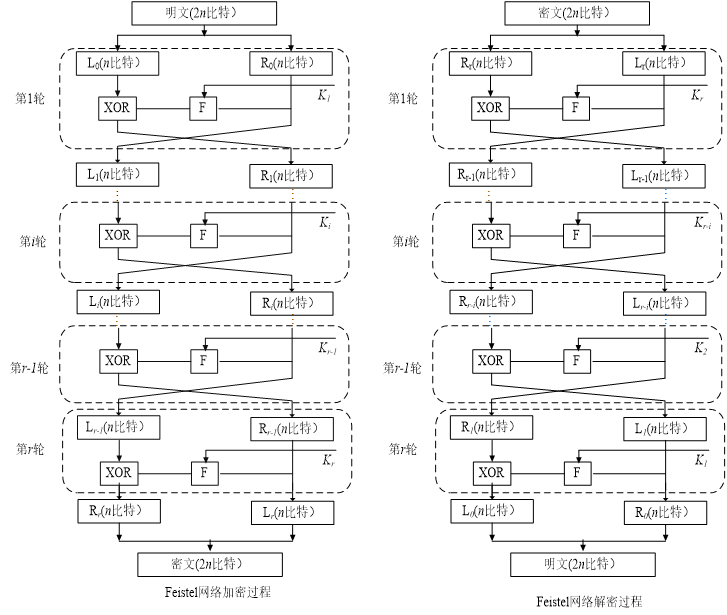
加密过程逻辑关系

\[L_{i}=R_{i-1}\\ R_{i}=L_{i-1}\oplus F(R_{i-1},k_{i}) \]

解密过程逻辑关系

\[R_{i-1}=L_i\\ L_{i-1}=R_{i}\oplus F(L_{i},k_{i}) \]

加密解密过程使用的是同一个F函数。

为了保证分组密码的安全性，与分组密码算法原则非常类似，Feistel网络结构实现与以下参数和特性有关：

• 分组大小：分组越大则安全性越高，但加密速度就越慢。分组密码设计中最为普遍使用的分组大小是64比特。
• 密钥大小：密钥越长则安全性越高，但加密速度就越慢。现在通常使用128比特的密钥长度。
• 轮数：多轮结构具有更高足够的安全性。一般轮数取为16。
• 子密钥产生算法：该算法的复杂性越大，则密码分析的困难性就越大。
• 轮函数（F）：轮函数的复杂性越大，密码分析的困难性也越大。

DES算法（数据加密标准）

基本属性

• 分组长度为64 bits (8 bytes)
• 密文分组长度也是64 bits。
• 密钥长度为64 bits，有8 bits奇偶校验位，有效密钥长度为56 bits。
• 加解密使用同一算法。
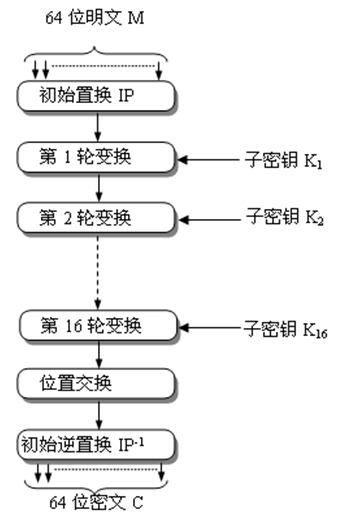
• 算法主要包括：初始置换IP、16轮迭代的乘积变换、逆初始置换\(IP^{-1}\)以及16个子密钥产生器。

总体流程图

初始置换

初始置换 \(IP^{-1}\)。将64 bit明文的位置进行置换，得到一个乱序的64 bit明文组，如下图，将原本在第58位的字符放到第1位；将原本在第50位的字符放到第2位，依次。置换完成后分成左右两段，每段为32 bit，以\(L_0\)和\(R_0\)表示。

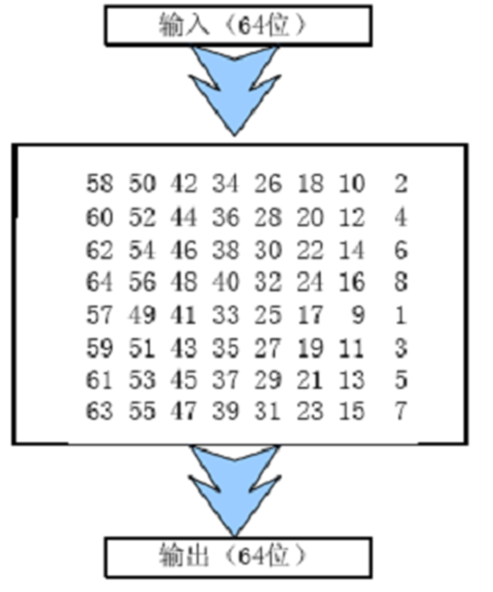
逆初始置换

逆初始置换 \(IP^{-1}\)将16轮迭代后给出的64 bit组进行置换，得到输出的密文组。输出为阵中元素按行读得的结果。

是IP的逆操作，满足\(Y=IP^{-1}(X)=IP^{-1}(IP(M))\)，比如刚才把第1位字符放到了第40位，现在就要换回来。

\(IP\) 和 \(IP^{-1}\) 在对加密意义上作用不大，它们的作用在于加密过程打乱原来输入的明文顺序。

密钥生成

密匙用于变换时参与F函数运算。

其中第8、16、......64位是奇偶校验位，不参与DES运算。

PC表示缩小选择换位（置换选择），LS表示循环左移，C、D表示密匙两个部分。

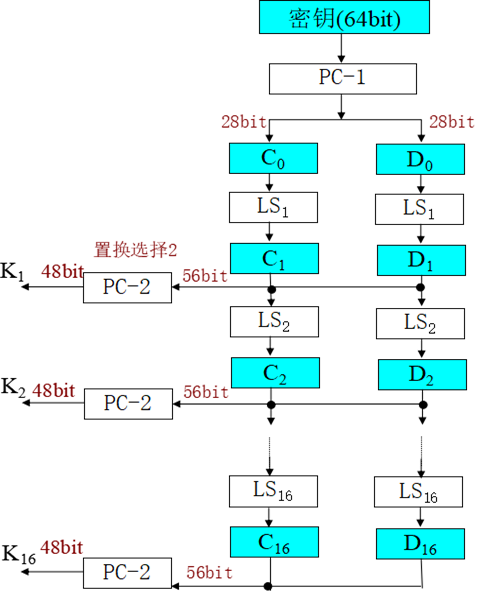
置换选择（PC）

轮结构（F变换）

DES采用了典型的Feistel结构，一次迭代过程图如下

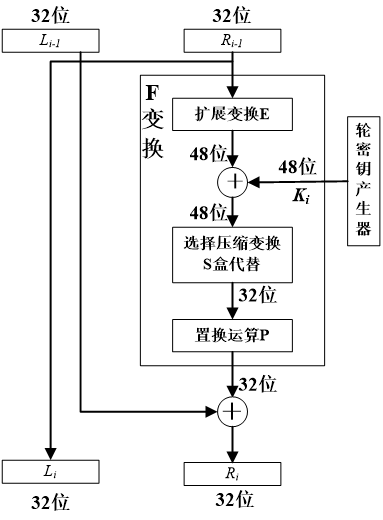
满足

\[L_{i}=R_{i-1}\\R_{i}=L_{i-1}\oplus F(R_{i-1},k_{i}) \]

F函数的变换过程如下，DES算法的安全性关键在于非线性函数F的性质。F以长度为32位的比特串作为输入，产生的中间结果为48位，并在最终产生长度为32位的比特串作为输出。

选择扩展运算 E盒

E-扩展运算是扩位运算，将32比特扩展为48比特，用方阵形式可以容易地看出其扩位其中粗方框中的为原始输入数据，边上的两列是扩展数据。最右列是第二列（原数据的第一列）向上循环移动一位，最左列是倒数第二列（原数据的最后一列）向下循环移动一位。

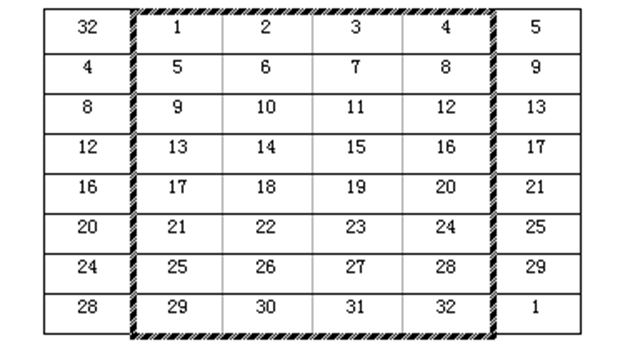
与子密钥异或

函数F将扩展置换得到的48位输出与子密钥 \(k_i\)（48位）进行异或运算。

S盒运算

S盒运算由8个S盒函数构成

\[S(x_1,x_2,\cdots ,x_{48})=S_1(x_1\cdots x_6)||S_2(x_7\cdots x_{12})||\cdots||S_8(x_{43}\cdots x_{48}) \]

其中，每一个S盒函数都是6比特的输入，4比特的输出。值就是对应表\(S_i\)中\((x_1x_6)_B\) （表示的二进制数）行和\((x_2x_3x_4x_5)_B\)列上的值。

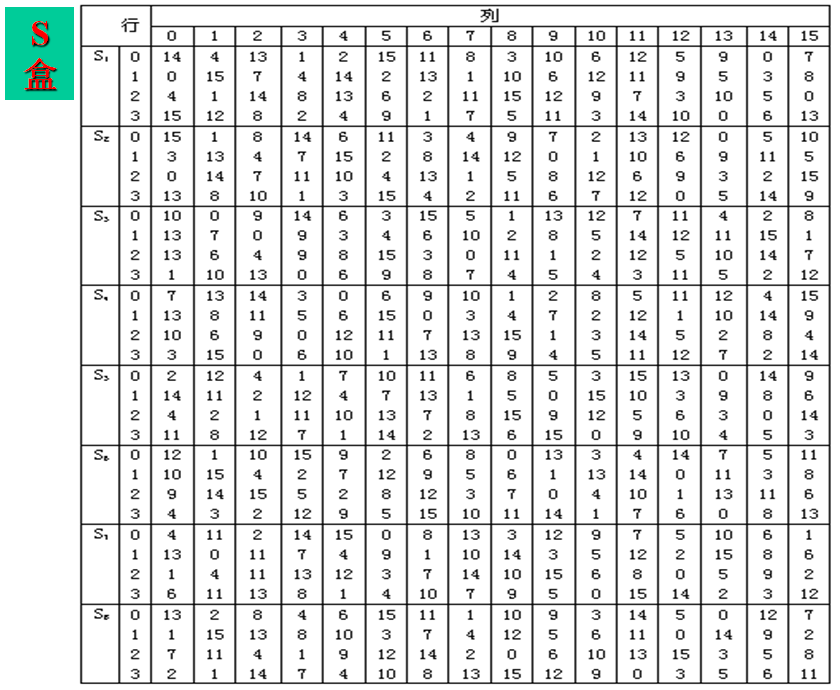
​ S盒是函数F的核心所在，同时，也是DES算法的关键步骤。实际上除了S盒以外，DES的其他运算都是线性的，而S盒是非线性的，它决定了DES算法的安全性。48位的比特串（分为8个6位分组）在经过8个S盒进行代替运算后，得到8个4位的分组，它们重新组合在一起形成一个32位的比特串。这个比特串将进行下一步运算：P盒置换。

P盒置换

P置换是对8个S盒的输出进行变换，可以扩散单个S-盒的效果，如下图所示，规则同 \(IP\) 和 \(IP^{-1}\)。

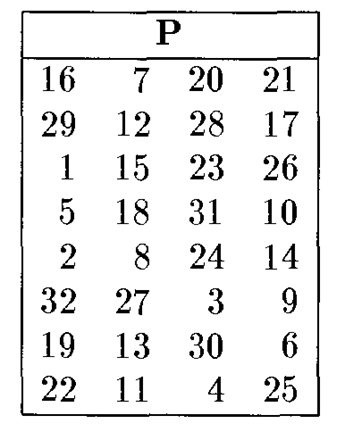
最后再来看一眼总流程，在执行16轮后，执行逆初始置换。

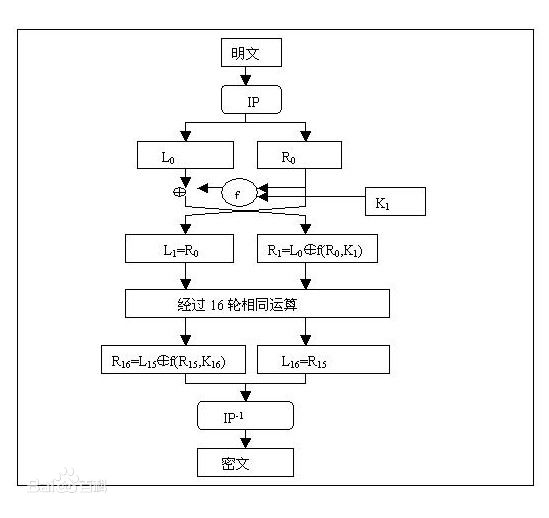
DES算法的解密

由于使用了Feistel网络结构，因此DES的解密和加密使用同一算法，但子密钥使用的顺序相反。

DES算法的安全性

​ DES运用了置换、替代、代数等多种密码技术，算法结构紧凑，条理清楚，而且加密与解密算法类似，便于工程实现。然而从DES诞生之日起人们就对它的安全性持怀疑态度，并展开了激烈的争论，主要的反对意见如下：

1. 对DES的S盒，迭代次数，密钥长度等的设计准则有争议

   ​ 因为DES算法中的参数都是固定的，人们担心若在算法是否存在后门，在这些争议中，对S盒的设计准则的质疑最为强烈。因为：除了S盒以外，DES中的所有运算都是线性的（如计算两个输出的异或，先形成两个输入的异或计算输出其结果都是相同的）。因此，S盒作为DES的非线性组件对安全性是至关重要的。

   ​ S盒的设计准则还没有完全公开，我们仍然不知道S盒的构造中是否使用了进一步设计的准则。这也使人们的猜测无法得到消除，关于S盒的争议仍在继续。关于S盒的设计，密码学家在这方面做出了许多工作，发表了大量的文献，可以参考一些文献获得进一步的知识。

2. DES存在一些弱密钥和半弱密钥

3. DES的56位有效密钥无法满足安全性要求

   ​ 1993年，R.Session和M.Wiener给出了一个非常详细的密钥搜索机器的设计方案，它基于并行的密钥搜索芯片，此芯片每秒测试\(5×10^7\)个密钥，当时这种芯片的造价是10.5美元，5760个这样的芯片组成的系统需要10万美元，这一系统平均1.5天即可找到密钥（最差情况：$ \dfrac {2^{56}-1}{24\times 60\times 60\times 5\times 10^{7}\times 5760} \approx 2.9 $，平均1.5），如果利用10个这样的系统，费用是100万美元，但搜索时间可以降到2.5小时。可见这种机制是不安全的。

   尽管DES有这样那样的不足，但是作为第一个公开密码算法的密码体制成功地完成了它的使命，它在密码学发展历史上具有重要的地位。

AES算法

太多了，这一段暂时不整理了。

对称密码体制的工作模式

ECB模式

​ 也叫电子码本模式，是最简单的模式，直接利用加密算法分别对分组数据组加密。明文分成64比特的分组进行加密，必要时填充，每个分组用同一密钥加密，同样的明文分组得到相同的密文。

ECB模式的特性：

• ECB运行模式在给定的密钥下，同一明文组总产生同样的密文组。
• 具有链接依赖性，各组的加密独立于其它分组，重排密文分组，将导致相应的明文分组重排。
• 具有无错误传播的特点，单个密文分组中有一个或多个比特错误只会影响该分组的解密结果。
• 安全性有限。由于同一明文产生同样的密文，这会暴露明文数据的格式和统计特征。

CBC模式

​ 也叫密码分组链接模式，比ECB模式实现复杂、更安全，因此它是最普遍使用的对称密码运行模式。CBC模式中加密过程第一个明文分组与初始矢量IV(Initial Vector)进行异或运算，而后面的明文分组和前一密文分组也做异或运算，再使用相同的密钥送至加密算法加密，形成一条链，这样每个明文分组的加密函数输入与明文分组之间不再有固定的关系。

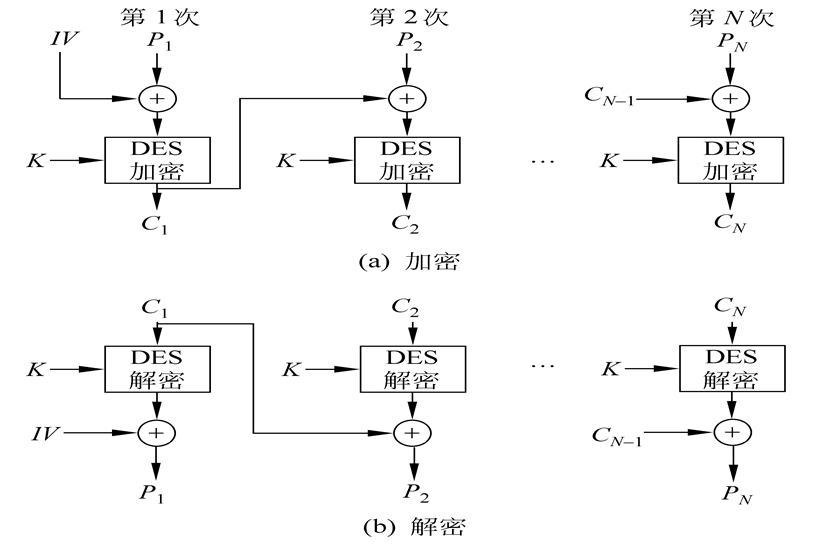
CBC模式的特性：

• CBC模式各密文分组不仅与当前明文组有关，而且通过反馈作用还与以前的明文组有关。在CBC模式下，最好是每发一个消息，都改变IV，比如将其值加1，这样即使是两个相同的明文使用相同的密钥，也将产生不同的密文，这样大大提高了安全性。

• 错误传播：若某组密文组\(C_j\)出错时，则会影响到分组\(C_j\)和\(C_{j+1}\)的解密（因为\(P_j\)依赖\(C_{j-1}\)和\(C_j\)，\(P_{j+1}\)依赖\(C_j\)和\(C_{j+1}\)），即该组恢复的明文\(P_j\)和下一组\(P_{j+1}\)，一般来说完全随机的（50%有错），因此若密文\(C_j\)有错，但\(C_{j+1}\)之后没有错误，\(C_{j+2}\)及后面的分组解密将不会受中错误比特的影响。

CFB模式

DES是分组长为64比特的分组密码。下图是CFB（Cipher Feed Back）模式示意图。设传送的每个单元（如一个字符）是\(j\)比特长，通常取\(j=8\)，与CBC模式一样，明文单元被链接在一起，使得密文依赖是前面所有的明文。

​ CFB模式的特性 ：

• 输入相同明文，改变IV会导致相同的明文输入得到不同的加密输出，IV无需保密。若待加密消息必须按字符(如电传电报)或按比特处理时，可采用CFB模式。CFB实际上是将加密算法DES作为一个密钥流产生器，因此操作模式使得我们能把分组密码定义为流密码。另外，CFB模式除能获得保密性外，还能用于认证。
• CFB与CBC的区别是反馈的密文长度为j，且不是直接与明文相加，而是反馈至密钥产生器。解密采用相同方案，但是使用加密函数而非解密函数。密文分组\(C_j\)依赖于\(P_j\)和前面的明文分组。
• 在CFB模式中，若一个或多个比特错误出现在r比特的密文组\(C_j\)中，则会影响到分组\(C_j\)和后续［n/r］个密文分组的解密（直到n个比特的密文被处理，在此之后出错的分组\(C_j\)完全移出移位寄存器）。例如，对于8位（1个字节）的加密，则会产生9字节的错误。

OFB模式

​ OFB（Output Feed Back）模式的结构类似于CFB，将分组密码算法作为一个密钥流产生器，其输出的j比特密钥直接反馈至分组密码的输入端，同时这j比特密钥和输入的j比特明文段进行异或运算，如下页图所示。不同之处如下：OFB模式是将加密算法的输出反馈到移位寄存器，而CFB模式中是将密文单元反馈到移位寄存器，克服了CBC和CFB的错误传播所带来的问题。

OFB模式的特性：

• 与CFB、CBC相同，输入相同明文，改变IV会导致相同的明文输入得到不同的加密输出。
• OFB模式的传输过程中的比特错误不会被传播。例如Cj中出现一个或多个比特错误，在解密结果中只有Pj受到影响，以后各明文单元则不受影响。
• 与CFB模式相比，更易受到对消息流的篡改攻击，比如在密文中取1比特的补，那么在恢复的明文中相应位置的比特也为原比特的补。因此使得敌手有可能通过对消息校验部分的篡改和对数据部分的篡改，而以纠错码不能检测的方式篡改，因此对于密文被篡改难以进行检测。

CTR模式

​ 计数器模式，与CFB、OFB模式类似，CTR（Counter）模式也可将分组密码转换为流密码，使用与明文分组规则相同的计数器长度产生密钥流，与明文分组进行异或。加密不同的分组所使用的计数器值必须不同，解密采用相同方案，但是使用加密函数而非解密函数。

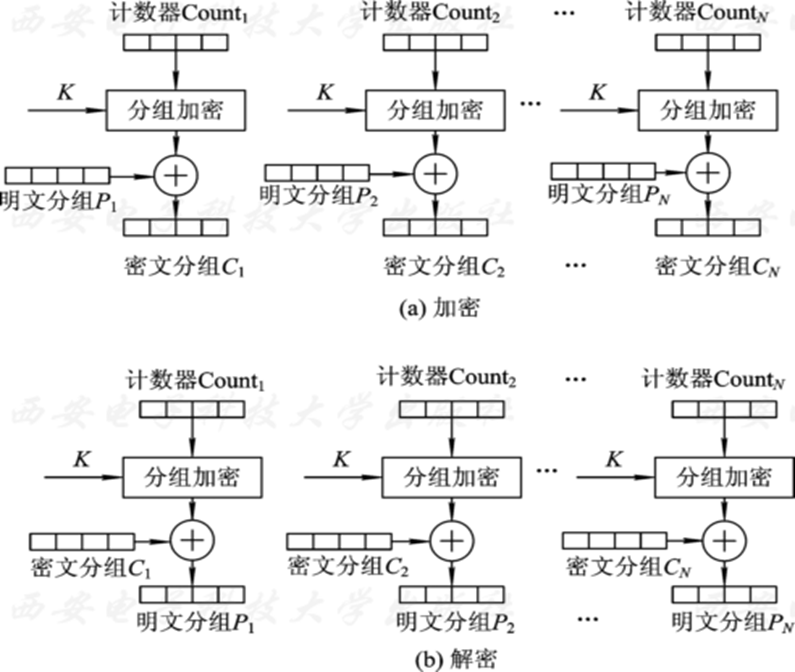
CTR模式的特性：

• CTR模式能够对多个分组的加、解密进行并行处理，进行异或之前的基本加密处理不依赖明文和密文的输入。
• CTR模式可以看做是OFB模式的一种简化，它使用计数器来更新输入分组，而不是反馈。
• 密文分组的处理与其它密文无关，实现简单。