基本代数概念与有限域下的椭圆曲线【密码学笔记】
群
群 \(G(group)\)是指由一个集合和一个二元运算 \(*\) (这里的 \(*\) 不是指乘法)构成的代数系,含有以下四个性质
- 群在 \(*\) 下的运算是封闭的
对于任意\(G\)中的两个元素,\(a\) 和 \(b\),\(a*b\) 也是 \(G\) 中的一个元素。
- 群中有一个元素 \(e\),称为单位元
对于群中的每个元素 \(a\) 都满足 \(a*e=e*a\)
- 群中每个元素都有逆元,记作\(a^{-1}\)
对于群中每个元素 \(a\) 都满足 \(a*a^{-1}=a^{-1}*a=e\)
- 群中运算都满足结合律
对于群中任意元素,\(a,b,c\) 都满足 \((a*b)*c=a*(b*c)\)
如果 \(G\) 满足交换律,则称群 \(G\) 为交换群或者阿贝尔群。
举个例子,整数集 \(Z\) 就是一个具有加法运算的群,也是阿贝尔群,\(0\) 位单位元,每个元素\(a\) 都有逆元 \(-a\),加法运算满足结合律。而整数集 \(Z\) 就不是一个具有乘法运算的群,因为元素 \(0\) 没有逆元。
每个群中的单位元都是唯一的,同时,群中每个元素的逆元也是唯一的,并且一个元素的逆元的逆元是该元素本身。\((a^{-1})^{-1}=a\)。
每当群中运算用于同一个元素与其自身相运算两次或多次时,可以采用指数运算来表示。这样就有 \(a^2=a*a\) ,\(a^{n}=a* a \ldots * a\),也就是说在整数集的加法运算下,\(a^2=a+a\),只是这不符合大家的习惯。
域
域 \(F\) 是一个含有至少两个元素的集合,含有两个二元运算称为 \(+\) 和 \(.\)(并不一定是我们通常意义上的加法和乘法),并满足以下性质:
- 集合 \(F\) 在 \(+\) 下是一个阿贝尔群,且具有单位元素 \(0\) 。
- 集合 \(F\) 在乘法下是封闭的,且域中所有非零元素构成的集合在乘法下是一个阿贝尔群
- 对于集合F中所有的\(a,b,c\),分配率 \((a+b)c=ac+bc\) 都成立。
有限域
若域中元素个数有限,则称 \(F\) 为有限域。并记作 \(F_q\) 或 \(GF(q)\) ,其中 \(q\) 为该有限域的元素个数,也叫做有限域的阶数。
例如,设 \(p\) 为素数,对于非空集合\(F=\{0,1, ...,p-1\}\),在模 \(p\) 的情况下做加法和乘法运算,定义运算规则为:
\(F\)关于加法构成交换群,加法单位元为\(0\);\(F\) 中全体非零元对乘法构成交换群,乘法单位元为1;分配率也成立。故 \(F\) 在定义的加法和乘法运算下构成有限域,用 \(GF(p)\) 或\(F_p\)表示。
例如,\(GF(2)\), 域中元素只有\(0,1\).域中运算为:\(1+1=0,1+0=1,0+1=1,0+0=0,1*1=1,1*0=0,0*1=0,0*0=0\).
域上的一元多项式
基本性质
数学家已经证明(好厉害哟),一个有限域 \(GF(k)\),其 \(k\) 必为 \(p\) 或者 \(p^m\) ( \(p\) 为素数),其它的 \(k\) 将不能构成有限域。 \(p^m\) ( \(p\) 为素数)的完全剩余集的每一个元素,可以使用 \(m\) 位的 \(p\) 进制数来表示,并进而可以使用多项式来表示。
令 \(a∈GF(p^m)\) ,则 \(a\) 可表示成如下次数为 \(m-1\) 的多项式
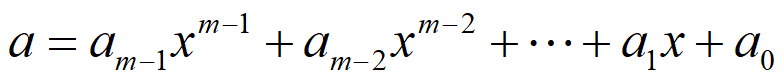
其中的系数 \(a_i\) 为模 \(p\) 的整数,\(x=p\),该表达式实质上是把一个整数用 \(m\) 位的 \(p\) 进制数来表示,系数 \(a_i\) 就是每一位的具体数字。
例如:在 \(GF(3^3)\) ,即\(GF(27)\)中,\(a=2x^2+x+2\)
表示成三位三进制数212,转换成十进制数为 \(2×3^2+1×3^1+2=23\)
多项式的运算
实质就是在 \(P\) 进制下的运算。

加法
举例:在\(GF(3^3)\)中,若\(a=2x^2+x+2,b=2x^2+2x+2\)
则有 \(c=a+b=x^2+1\)
减法
在有限域内,做减法,就是需要注意,对负数取模(模数为正时),结果一定是正的。
举例:在\(GF(3^{3})\)中,若 \(a=2x^2+x+2\),\(b=2x^2+2x+2\)
则有 \(c=a-b=2x\)
乘法
在\(GF(3^{3})\)中,若 \(a=2x^2+x+2\),\(b=2x^2+2x+2\),求 \(ab\) 的过程如下
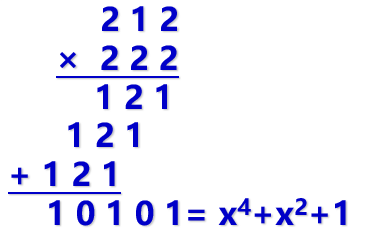
得 \(d=ab=x^4+x^2+1\)
计算过程中没有进位一说,每一步都进取模操作。
除法
求\(x^4+x^2+1\), 除以\(x^3+2x+1\)
\(x^4+x^2+1——10101\)
\(x^3+2x+1——1021\)
二者相除,得到的余数为\(221\),则计算结果为\(2x^2+2x+1\)。
和乘法相类似,计算过程中也没有借位一说,出现负数就进行取模。
椭圆曲线
椭圆曲线是形如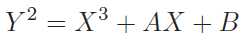 的方程的解集,这种方程式被叫做\(Weierstrass\)方程。例如:
的方程的解集,这种方程式被叫做\(Weierstrass\)方程。例如:

椭圆曲线的一个特点是能够用椭圆曲线上的两个点“相加”生成第三个点。
之所以用“相加”来表示,是因为这个操作在某些方面类似于加法操作。用几何学来描述“相加”操作,设 \(P\) 和 \(Q\)为椭圆曲线 \(E\) 上的两个点,若通过\(P,Q\)两点的直线交 \(E\) 于 \(R\) ,若 \(R'\) 为 \(R\) 关于 \(x\) 轴的对称点,则记 $ P\oplus Q=R' $。

例如:
设椭圆曲线E为 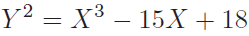 ,点P为(7,16),点Q为(1,2)。
,点P为(7,16),点Q为(1,2)。
由两点可以得出直线L: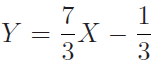 ,为得到E和L的交点,我们计算
,为得到E和L的交点,我们计算
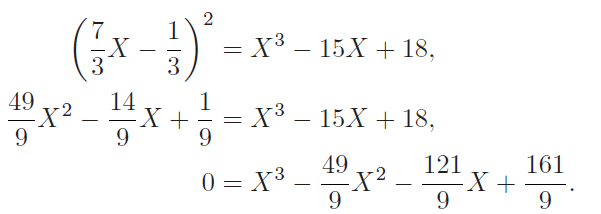
我们需要得到方程式的根,由于我们已经知道X=7和X=1,所以有
从而得到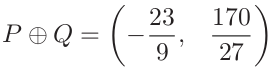
那么当我们想要得到 \(P\oplus P\) 时,应该怎么做呢?
设 \(P\) 为椭圆曲线 \(E\) 上的两个点,若通过\(P\) 的一条切线交 \(E\) 于 \(R\),若 \(R'\) 为 \(R\) 关于 \(x\) 轴的对称点 ,则记 $2P = P\oplus P=R' $。
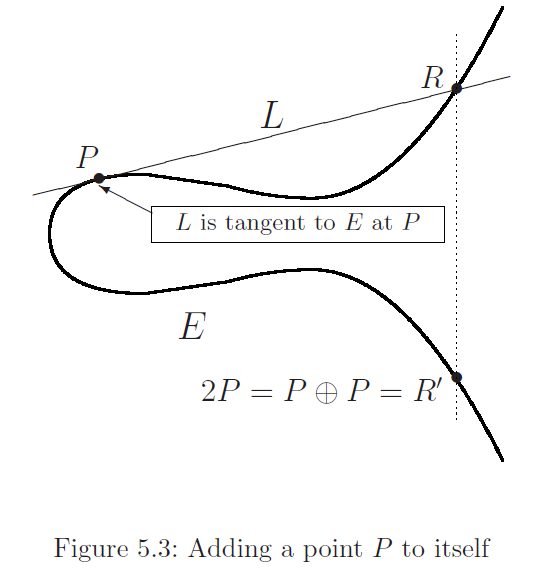
例如:
设椭圆曲线为 ,点P为(7,16) 。计算 \(P\oplus P\) 。
,点P为(7,16) 。计算 \(P\oplus P\) 。
通过隐式微分方程求解:
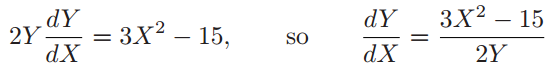
由于P=(7,16),得到斜率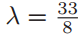 ,所以
,所以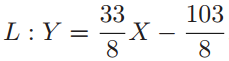
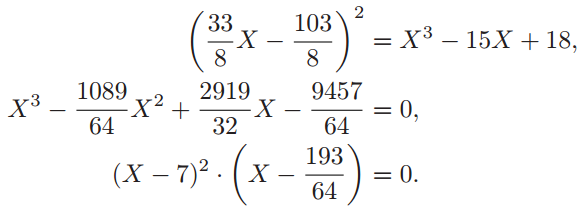
注意P的X轴坐标X=7为3次多项式的2重根,得到
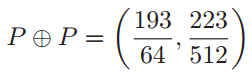
当然椭圆曲线上的“相加法则”也存在着一个潜在的问题。如果我们尝试做\(P=(a,b)\)点关于x轴的对称点\(P’=(a,-b)\)。那么通过\(P\)和\(P’\)的直线\(L\)是垂直线\(x=a\),这条线与\(E\)的交点只有\(P\)和\(P’\)。
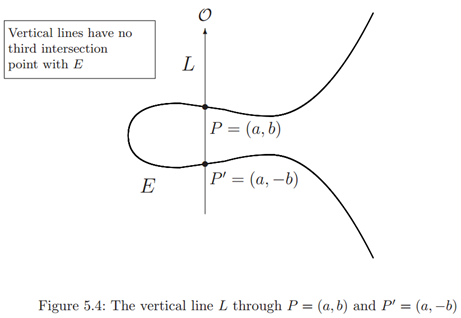
基于 \(P\oplus P'\) ,有一种解决办法就是创造一个额外的点\(O\) (无穷远处),这个点不存在在XY平面中,但是我们假设它存在在每一垂直线上。所以有\(P\oplus P'=O\),从而可以得出\(P\oplus O=P'\),所以\(O\)在椭圆曲线加法中相当于零。
相关定义:
椭圆曲线E为\(Weierstrass\)方程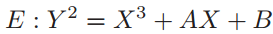 的所有解以及点\(O\)所构成的集合,其中常量A和B满足:
的所有解以及点\(O\)所构成的集合,其中常量A和B满足:
-
\(4A^3+27B^2\neq 0\),书上没有证明,这个俺不会,就跟一元二次方程里的\(\Delta = b^2-4ac\) 一样,数学家证明过了。
-
\(P,Q\)为椭圆曲线\(E\)上的两个点,直线\(L\)过\(P\)和\(Q\)两点,或为当\(P=Q\)时在\(P\)点的切线。这时\(L\)和\(E\)有\(P,Q,R\)三个交点,同时认为\(O\)位于每一垂直线上。设\(R=(a,b)\),\(P\)和\(Q\)的和被定义为\(R\)关于\(x\)轴的对称点\(R’=(a,-b)\),写成 \(P\oplus Q\)或\(P+Q\)。
-
进一步,若\(P=(a,b)\),那么\(P\)点的反射点为 \(\ominus P=(a,-b)\),或写成\(-P\),我们定义 \(P\ominus Q\) 或\(P-Q\) 或\(P\oplus (\ominus Q)\)
-
相似的,连加可以表示为点与整数的乘积:
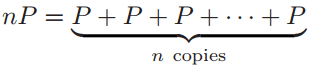
定义中 \(\Delta _E=4A^3+27B^2\) 叫做 \(E\) 的判别式。\(\Delta _E\neq 0\) 等价于3次多项式 \(X^3+AX+B\) 没有重复根。我们可以把多项式改成 \(X^3+AX+B=(X-e_1)(X-e_2)(X-e_3)\) ,那么\(4A^3+27B^2\neq 0\),当且仅当\(e_1、e_2、e_3\)互不相等。
定理1:
椭圆曲线E上的加法满足以下性质:
-
存在单位元:\(P+O=O+P=P\)
-
可逆:\(P+(-P)=O\)
-
满足结合律:\((P+Q)+R=P+(Q+R)\)
-
满足交换律:\(P+Q=Q+P\)
定理2:
椭圆曲线加法算法:
设椭圆曲线\(E:Y^2=X^3+AX+B\)上两点为\(P_1\)和\(P_2\):
(a) 如果\(P_1=O\),则\(P_1+P_2=P_2\)。
(b) 否则,如果\(P_2=O\),则\(P_1+P_2=P_1\)。
(c) 否则,记\(P_1=(x_1,y_1)\),\(P_2=(x_2,y_2)\)。
(d) 如果\(x_1=x_2\)且\(y_1=-y_2\),则\(P_1+P_2=O\)。
(e) 否则,定义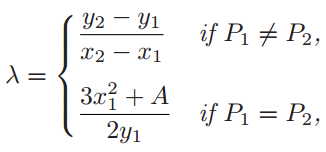
并设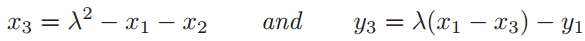
则\(P_1+P_2=(x_3,y_3)\)
这个书上有证明,这个俺会了,但是不想写。
有限域上椭圆曲线
为了将椭圆曲线应用到密码学中,需要这样一种椭圆曲线,其上的点的坐标在有限域\(F_p\)中。我们定义一种在有限域\(F_p(p>3)\)上的椭圆曲线:
\(E:Y^2=X^3+AX+B,A,B∈F_p\) ,其判别式满足\(4A^3+27B^2(mod\ p)\neq\ 0\)。记为:\(E_p(A,B)\)
\(E\)上的点的坐标在\(F_p\)中记为:
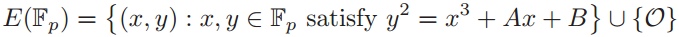
例如:
域\(F_{13}\)上的椭圆曲线\(E:Y^2=X^3+3X+8\)。
我们将所有可能的\(X=0,1,2,…,12\)代入\(X^3+3X+8\)并检查哪些值是模\(13\)的二次剩余。例如,将\(X=0\)代入,得到\(8\),而\(8\)不是模\(13\)的二次剩余;再将\(X=1\)代入,得到\(12\),由于\(5^2≡12(mod\ 13)\)和\(8^2≡12(mod\ 13)\),所以\((1,5)\)和\((1,8)\)在\(E(F_{13})\)中。依此计算最终得到:
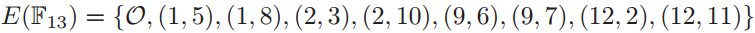
定理3
设\(E\)是\(F_p\)上的椭圆曲线,\(P\)和\(Q\)是\(E(F_p)\)中的点。
(a). 对\(P\)和\(Q\)应用椭圆曲线加法算法(定理2)可以得到一个\(E(F_p)\)中的点,记为\(P+Q\)。
(b). \(E(F_p)\)上的加法满足定理1列举的所有性质。也就是说,加法使\(E(F_p)\)成为一个有限群。
证明:
定理2 (e)的公式是通过将过P和Q直线的方程代入E求解X而导出的,从而加法的结果必然是E上的点,也就是方程所定义的E的解,所以(a)为真;对于(b),存在单位元由加法算法的步骤(a)和(b)得到,可逆由加法算法的步骤(d)得到,满足交换律很容易得到,因为可以很简单的验证:如果将两点交换,加法算法会得到相同的结果。但满足结合律不是很容易说明。可以通过加法算法公式直接验证,但要考虑很多特殊情况。
例如:
域\(F_{13}\)上的椭圆曲线\(E:Y^2=X^3+3X+8\)。我们使用加法算法(定理2)在\(E(F_{13})\)中将\(P=(9,7)\)和\(Q=(1,8)\)两点相加。根据算法步骤(e)首先计算
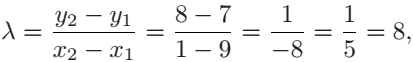
注意所有的计算都在域\(F_{13}\)上,所以\(-8\ mod\ 13=5\)且\(1/5=5^{-1}=8\) (数论倒数)。下一步我们计算
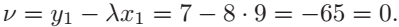
最后,根据加法算法我们计算
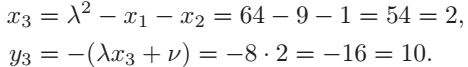
这样就得到
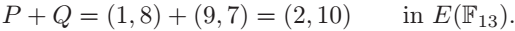
相似地,我们可以使用加法算法将\(P=(9,7)\)自身相加。注意所有的计算都在域\(F_{13}\)上,我们得到
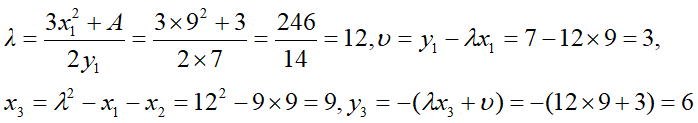
所以在域\(F_{13}\)上\(P+P=(9,7)+(9,7)=(9,6)\)。相似地,我们计算\(E(F_{13})\)上每一对点的和。计算结果如下表: