数据结构篇——二叉排序（查找，搜索）树

引入

基本性质：

二叉排序树（又叫二叉搜索、查找树) 是一种特殊的二叉树，定义如下：

若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
左、右子树也分别为二叉排序树。
不允许有键值相同结点。【如果真的出现了，那么放在左子树，右子树是无所谓的】

二分查找与二叉排序树

二分查找也称为折半查找，要求原线性表有序，它是一种效率很高的查找方法。如果在需要进行频繁修改的表中采用二分查找，其效率也是非常低下的，因为顺序表的修改操作效率低。如果只考虑频繁的修改，我们可以采用链表。然而，链表的查找效率又非常低。综合这两种数据结构的优势，二叉查找树(Binary Sort/Search Tree)登场了。

给定一串数\(（65,32,87,46,71,98,39）\)，使用插入构造法，步骤如下：

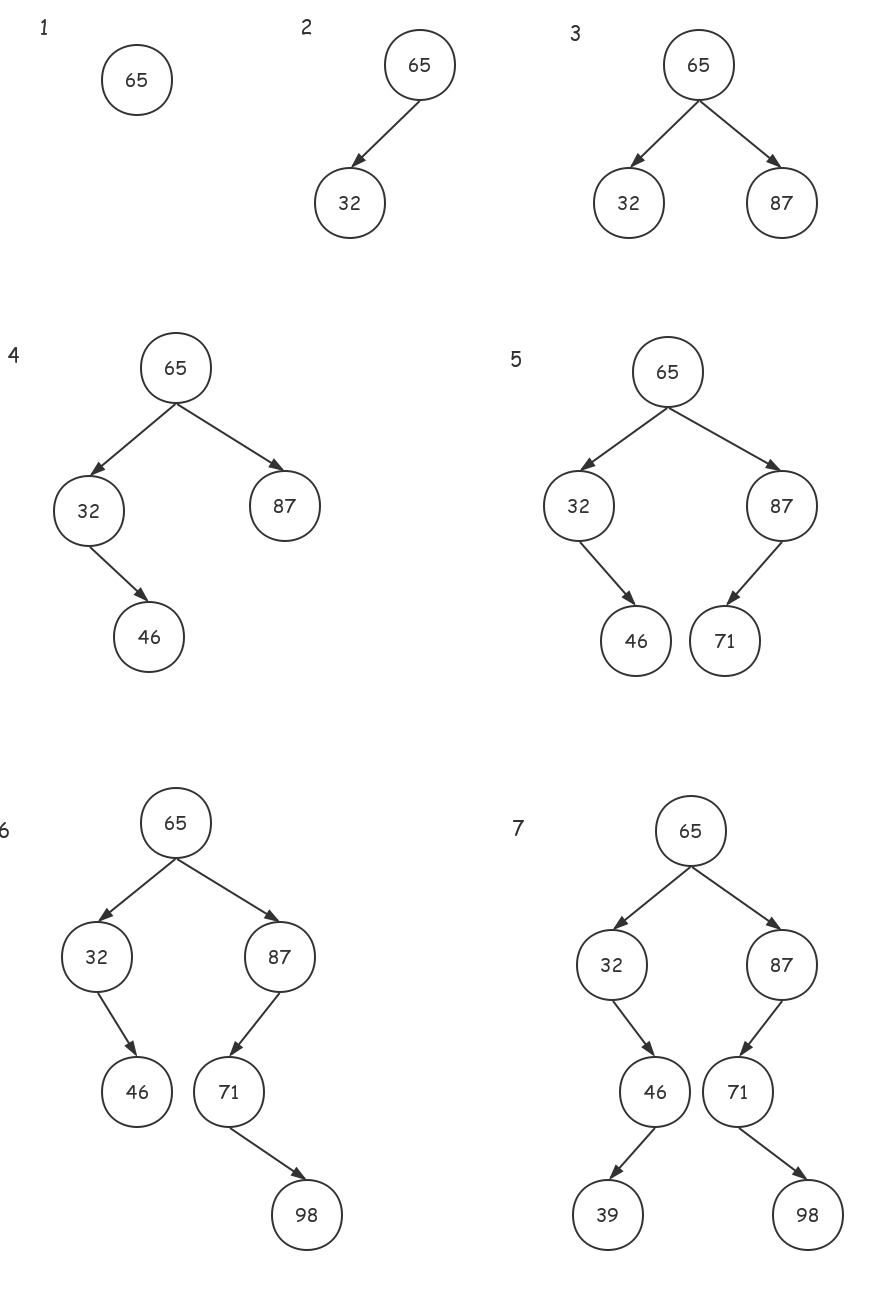
二叉排序树的基本操作

结构体定义

typedef struct BTNode
{
	char data;
	struct BTNode* Left;
	struct BTNode* Right;
}*BTree;

typedef BTNode BSTNode, *BSTree;

查找节点

如果是普通二叉树的查找操作，因为无法确定二叉树的具体特性，因此只能对其左右子树都进行遍历。但二叉排序树的特性，则会有一条确定的路线。

//找不到返回NULL，找到返回该节点。
//递归
BSTNode* BSTreeFind(BSTree t, int x) {
	if (!t)return NULL;
	if (t->data == x) return t;
	if (x < t->data) return BSTreeFind(t->Left, x);
	if (x > t->data) return BSTreeFind(t->Right, x);
}
//非递归
BSTNode* BSTFind(BSTree T,int x) {
	BSTree p = T;
	while (p) {
		if (x == p->data)
			return p;
		p = x > p->data ? p->Right : p->Left;
	}
	return NULL;
}

插入节点

对于一颗二叉排序树来说，如果查找某个元素成功，说明该结点存在；如果查找失败，则查找失败的地方一定就是该结点应该插入的地方。

BSTree InsertBStree(BSTree BST, int x) {
	if (BST == NULL) {
		BST = new BSTNode;
		BST->data = x;
		return BST;
	}
	if (x < BST->data)
		BST->Left = InsertBStree(BST->Left, x);
	else
		BST->Right = InsertBStree(BST->Right, x);
	return BST;
}

二叉排序树的建立

建立一颗二叉排序树，就是先后插入\(n\)个结点的过程，与一般二叉树的建立是完全一样的。

BSTree BuildBSTree(int* a, int length) {
	BSTree BST = NULL;
	for (int i = 0; i < length; i++)
		BST = InsertBStree(BST, a[i]);
	return BST;
}

二叉排序树的删除

二叉查找树的删除操作一般有两种常见做法，复杂度都是\(O(h)\)或\(O(log(n))\)，其中 \(h\) 为树的高度，\(n\) 为结点个数。

如下图的二叉排序树，如果要删除结点 \(5\)，则有两种办法，一种办法是以树中比 \(5\) 小的最大结点（结点 \(4\) ）覆盖结点 \(5\) ，另一种是用树中比 \(5\) 大的最小结点（结点 \(6\) ）覆盖结点 \(5\)。

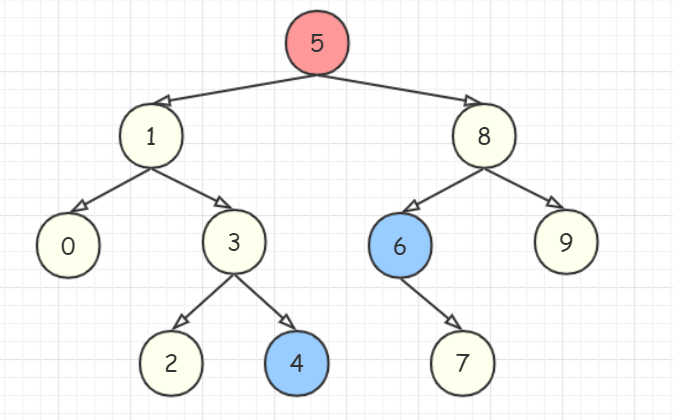
在二叉排序树中把比该结点权值小的最大结点称为该结点的前驱，把比该结点权值大的最小结点称为该结点的后继。结点的前驱是左子树的最右结点，结点的后继是右子树的最左结点。用下面两个函数用来寻找以root为根的树中最大、最小权值的结点，后面会使用到。

//获得以root为根结点的树中的最大值结点
int GetMax(BSTree root) {
	while (root->Right != NULL)
		root = root->Right;
	return root->data;
}

//获得以root为根结点的树中的最小值
int GetMin(BSTree root) {
	while (root->Left != NULL) {
		root = root->Left;
	}
	return root->data;
}

假设决定使用结点\(N\)的前驱 \(P\) 来替换 \(N\) ，于是就把问题转换为，先用 \(P\) 的值去覆盖 \(N\) 的权值，再删除结点\(P\)，于是删除操作的实现如下：（写法1好理解，写法2更简洁）

写法1：

使用 BSTree root，如果 root 为要删除的结点， \(P\) 为父节点，删除情况有以下3种：

　　1. root 结点是叶子，将 \(P\) 节点的 left 或 right 指针域置为NULL。

　　2. root 结点只有左子树，将 root 节点的 left 重新到结点 \(P\) 上。和删除单链表节点类似。（只有右子树时情况相似。第一种情况，写的时候可以和第二种合并起来）

　　3. root 结点既有左子树，也有右子树，寻找结点的前驱 pre（或者后继），用 pre 的值去覆盖 root 的权值，再删除结点 pre，而这个 pre 的删除一定属于情况 1 或者 2 。

这个写法更适合JAVA，代码里的那些 delete 还可以省去，但是必须要注意的是：函数的返回值不是多余的，删除只有一个（或没有）子树的根节点的时候，必须用到这个返回值。

实现方法1：

//删除结点左子树的最大值结点
BSTree DelMax(BSTree root) {
    if (root->Right == NULL) {
        BSTNode *t= root->Left;
        delete root;
        return t;
    }
    root->Right = DelMax(root->Right);
    return root;
}

BSTree BSTDel(BSTree root,int x) {
    if (root == NULL) 
        return NULL;
    if (root->data == x) {
        //情况1和2，被删除的结点只有左子树或右子树，或没有子树
        if (! root->Right || !root->Left) {
            BSTNode *t = !root->Right ? root->Left : root->Right;
            delete root;
            return t;
        }
        //删除既有左子树，也有右子树的结点
        else{
            root->data = GetMax(root->Left);
        	root->Left = DelMax(root->Left);
        }
    }
    else if (x > root->data) 
        root->Right = BSTDel(root->Right, x);
    else  
        root->Left = BSTDel(root->Left, x);
    return root;
}

实现方法2：

//删除子树中的最大值
void DelMax(BSTree &root,int &value) {
	if (!root)return;
	if (root->Right == NULL) {
		BSTNode *t= root;
		value = root->data;
		root = root->Left;
		delete t;
	}
	else
		DelMax(root->Right, value);
}

void BSTDel(BSTree &root,int x) {
	if (root == NULL) 
		return;
	BSTree p = root;
	if (p->data == x) {
		if (! p->Right || !p->Left) {
			root = !p->Right ? p->Left : p->Right;
			delete p;
		}
		else
			//因为使用的方法是值替换，并没有把原来的root覆盖掉，所以delete p不能像和下面方法2一样写在整个大if里
			DelMax(root->Left, root->data);
	}
	else if (x > p->data) BSTDel(p->Right, x);
	else  BSTDel(p->Left, x);
}

写法2：

使用 BSTree *root，和上面的BSTree &root是等价的，如果 root 为要删除的结点，删除情况也是以下3种：

　　1. 当前 `root` 结点是叶子，将 `root` 置空。
　　2. `root` 结点只有左子树，将 `root` 置为 `root->Right`（只有右子树时情况相似。第一种情况，写的时候可以和第二种合并起来）
　　3. 被删除的结点既有左子树，也有右子树，寻找结点的前驱 `pre`（或者后继），用 `root` 的指针域覆盖 `pre` 的指针域，再把结点 `root` 删除。（形象化来说就是删除 `root`，把 `pre` 移动到 `root` 的位置）

void BSTDel(BSTree *root, int x){
    if (!*root) return; 
    BSTree p = *root;
    if (p->data == x) {
        if (!p->Right || !p->Left)
        	*root = !p->Right ? p->Left : p->Right;
        else{
                BSTNode *parent = p->Left, *q = p->Left;
                if (!q->Right) q->Right = p->Right;
                else {
                    while (q->Right) {
                        parent = q;
                        q = q->Right;
                    }
                    parent->Right = q->Left;
                    q->Left = p->Left;
                    q->Right = p->Right;
                }
                *root = q;
        }
        delete p;
    }
    else if (x > p->data) //向右找
        BSTDel(&(p->Right), x);
    else if (x < p->data) //向左找
        BSTDel(&(p->Left), x);
}

二叉排序树的性质

二叉排序树最基本的性质：二叉排序树的中序序列是有序的。

如果合理调整二叉排序树的形态，使得树上的每个结点都尽量有两个子结点，这样整个二叉树的高度就会大约在\(log(n)\) 左右，其中 \(n\) 为结点个数。实现这个要求的一种树就是下一篇平衡二叉树（AVL Tree）。

posted @ 2019-11-02 23:53 czc1999 阅读(837) 评论(1) 编辑收藏举报

刷新页面返回顶部

czc1999