数据结构篇——二叉树
引入
在数据结构中,将现实生活中的树根抽象为根节点(Root)树叉抽象为结点(Node),将叶子抽象为(Leaf),将树枝抽象为边(Edge),且一条边只用来连接两个结点,互为父子节点。
二叉树的性质
二叉树
-
树可以没有结点,这种情况下把树称为空树。
-
树的层次从根节点开始算,即根节点算第\(1\)层。【也有的教材规定根结点在第\(0\)层,这里全部以\(1\)层为准】
-
把结点的子树颗数称为结点的度(degree),树中所有结点的最大的度称为树的度(也叫做树的宽度)。
-
由于一条边连接两个结点,且树中不会存在环,因此对于有\(n\)个结点的树,边树一定是\(n-1\)。
-
结点的深度是指从根节点(深度为\(1\))开始自顶向下逐层累加至该结点时的深度值;结点的高度是指从最底层叶子结点(高度为\(1\))开始自底向上逐层累加至该结点时的高度值。树的深(高)度是结点的最大深(高)度,所以对树而言,深度和高度一定是相等的。
-
对于任何一棵非空的二叉树,如果叶节点个数为\(n_{0}\),度数为\(2\)的节点个数为\(n_2\),则有: $n_0 = n_2 + 1 $
在一棵二叉树中,除了叶子结点(度为\(0\))之外,就剩下度为\(2(n_2)\)和\(1(n_1)\)的结点了。在二叉树中结点总数为\(T\),\(T = n_0+n_1+n_2\);而总度数为\(T-1\)。所以有:\(n_0+n_1+n_2-1 = 2*n_2 +n_1\);得\(n_0 = n_2+1\);
完全二叉树
- 除了最下面一层之外,其余的结点数都达到了本层能达到的最大结点数。且最下面一层从左至右连续存在若干结点。
- 本质上还是一颗二叉树,适用二叉树的所有不与1矛盾的性质。
满二叉树:
- 每一层的节点数都达到了本层能达到的最大结点数。
- 本质上还是一颗完全二叉树,适用所有完全二叉树不与1矛盾的性质。

二叉树的存储结构
二叉树
一般来说,二叉树的数据结构定义为二叉链表,两个指针域分别指向左子树和右子树,不存在指向NULL。
typedef struct BTNode
{
char data;
struct BTNode* Left;
struct BTNode* Right;
}*BTree;
完全二叉树
对于完全二叉树,它完全可以也采用上面的二叉链表存储,但由于其特性,还可以有更便捷的存储方法。对于一个完全二叉树,如果对所有结点按层次、左右顺序编号,规定根结点编号为\(1\),对任一层的节点\(k(1<=k<=n)\)
- 结点\(k\)的左孩子为\(2*k\)
- 右孩子为\(2*k+1\)
- 如果有父节点(\(k>1\)),父节点为 \(k / 2\) 下取整。
也就是说完全二叉树可以通过建立一个大小为\(n\)的数组来存放所有节点的信息。
而且事实上,即便不是完全二叉树,可以将其视为完全二叉树,用一个特殊值(比如 \(-1\) )表示空节点即可,但这样空间消耗十分巨大。
二叉树的遍历
二叉树的遍历是指通过一定顺序访问二叉树的所有节点。二叉树的有四种遍历方式,先、中、后序遍历,“先、中、后”表示根结点的遍历次序。此外,还有一种层次遍历。其中前三种一般使用DFS实现,层次遍历一般使用BFS实现。
先序遍历
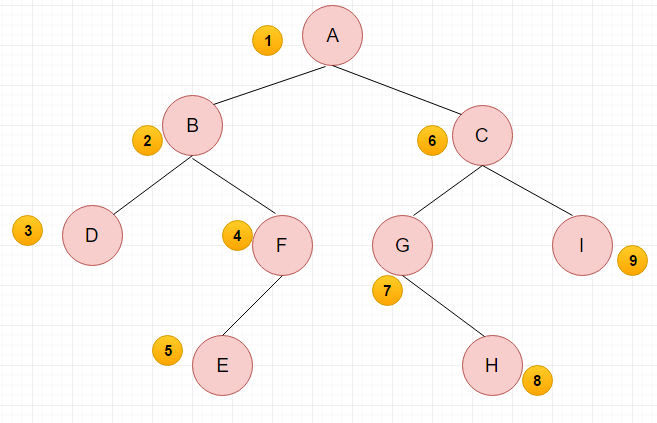
先遍历分支的根结点,再遍历左子树,最后遍历右子树。
先序序列:\(ABDFECGHI\)
递归实现
void Preorder(BTree t) {
if (!t)return;
cout << t->data << " ";
Preorder(t->Left);
Preorder(t->Right);
}
非递归实现
对于任一结点p:
- 访问该结点p,并将结点p入栈;
- 判断结点p的左孩子是否为空,若为空,则取栈顶结点并进行出栈操作,并将栈顶结点的右孩子置为当前的 结点p,循环置a;若不为空,则将p的左孩子置为当前结点p;
- 直到p为空,并且栈为空,则遍历结束。
void preorderUnRecur(BTree T) {
stack<BTree>s;
s.push(T);
while (!s.empty()) {
T = s.top();
s.pop();
cout << T->data << " ";
if (T->Right)
s.push(T->Right);
if (T->Left)
s.push(T->Left);
}
cout << endl;
}
先序序列性质
由于先序序列优先访问根结点,因此对于一颗二叉树的先序序列来说,序列的第一个一定是根结点,对子树同样适用。
中序遍历
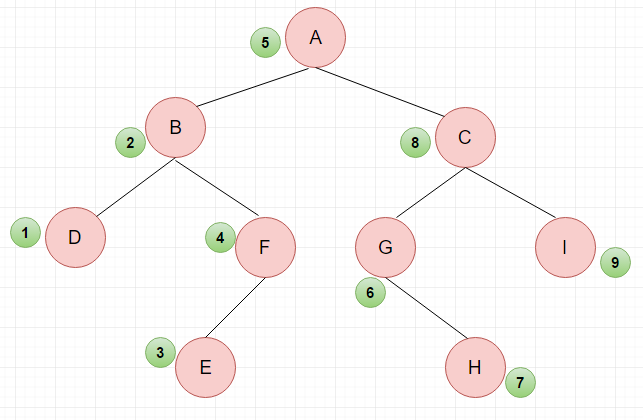
先遍历左子树,再遍历根结点,最后遍历右子树。
中序序列:\(DBEFAGHCI\)
递归实现
void Inorder(BTree t) {
if (!t)return;
Inorder(t->Left);
cout << t->data << " ";
Inorder(t->Right);
}
非递归实现
对于任一结点:
- 若其左孩子不为空,则将p入栈,并将p的左孩子设置为当前的p,然后对当前结点再进行相同的操作;
- 若其左孩子为空,则取栈顶元素并进行出栈操作,访问该栈顶结点,然后将当前的p置为栈顶结点的右孩子;
- 直到p为空并且栈为空,则遍历结束。
void inorderUnRecur(BTree T) {
if (!T)return;
stack<BTree>s;
while (!s.empty() || T) {
if (T) {
s.push(T);
T = T->Left;
}
else {
T = s.top(); s.pop();
cout << T->data << " ";
T = T->Right;
}
}
cout << endl;
}
中序序列性质
由于中序序列总是把根结点放在左子树和右子树中间,所以只要知道根结点在哪个位置,就可以通过根结点在中序序列中的位置区分出左子树和右子树。对子树同样适用。
比如中序序列:\(DBEFAGHCI\),\(A\)为根结点,则一定可以知道,树中\(DBEF\)一定是\(A\)的左子树部分,而\(GHCI\)一定是\(A\)的右子树部分。
后序遍历
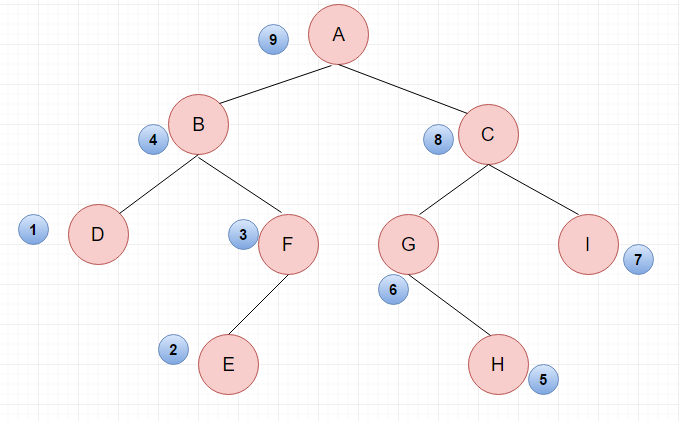
先遍历分支的左子树,再遍历右子树,最后遍历根结点。
后序序列:\(DEFBHGICA\)
递归实现
void Postorder(BTree t) {
if (!t)return;
Postorder(t->Left);
Postorder(t->Right);
cout << t->data << " ";
}
非递归实现
在后序遍历中,要保证左孩子和右孩子都已被访问,并且左孩子在右孩子之前访问才能访问根结点,对于任一结点p,先将其入栈。再将p的右孩子和左孩子依次入栈,这样就保证了每次取栈顶元素的时候,左孩子在右孩子之前别访 问,左孩子和右孩子都在根结点前面被访问。
使用两个栈 A,B,想要输出LRN的后序序列,那么压栈顺序就得是NRL,程序如下,用栈来做宽搜,大二下算法课学过,当时完全懂这玩意有鸟用,但总会有一些访问顺序的要求是这么特殊的。
void postorderUnRecur(BTree T) {
if (!T)return;
stack<BTree>A,B;
s1.push(T);
while (!A.empty()) {
T = A.top(); A.pop();
B.push(T);
if (T->Left)A.push(T->Left);
if (T->Right)A.push(T->Right);
}
while (!B.empty()) {
cout << B.top()->data << " ";
B.pop();
}
cout << endl;
}
后序序列性质
后序序列总是把根结点放在最后访问,这和先序序列正好相反,因此对于后序遍历来说,序列的最后一个结点一定是根结点。对子树同样适用。
层次遍历
层次遍历是指自上而下的顺序从根结点向下逐层进行遍历,宽搜。
void LevelTraversal(BTNode* root) {
queue<BTNode*> Q;
Q.push(root);
while (!Q.empty()) {
BTNode* T = Q.front();
Q.pop();
cout << T->data << " ";
if (T->Left) {
Q.push(T->Left);
}
if (T->Right) {
Q.push(T->Right);
}
}
}
中序序列+xx序列构建二叉树
给定包含中序序列的两个序列(也包括层序序列,代码没有写)可以重建出唯一的二叉树(不包含中序序列的两个、甚至三个序列创建出的二叉树不唯一)。
BTree BuildTree_pre_in(char* pre, char* in, int length) {
if (length == 0)
return NULL;
BTree BT = new BTNode;
BT->data = *pre;
int rootIndex = 0;
//先序序列的首个结点,是当前树的根结点
while (in[rootIndex] != *pre)
rootIndex++;
//刚才找到的结点,在中序序列中,它左边的部分是它的左子树,右边的部分是它的右子树,。
BT->Left = BuildTree_pre_in(pre + 1, in, rootIndex);
BT->Right = BuildTree_pre_in(pre + rootIndex + 1, in + rootIndex + 1, length - (rootIndex + 1));//因为rootIndex是下标,所以这里都要+1
return BT;
}
BTree BuildTree_in_post(char* in, char* post, int length) {
if (length == 0)
return NULL;
BTree BT = new BTNode;
BT->data = *(post + length - 1);
int rootIndex = length - 1;
//当前子树后序序列的最后一个结点,是当前子树的根。
while (in[rootIndex] != *(post + length - 1))
rootIndex--;
//刚才找到的结点,在中序序列中,它左边的部分是它的左子树,右边的部分是它的右子树。
BT->Left = BuildTree_in_post(in, post, rootIndex);
BT->Right = BuildTree_in_post(in + rootIndex + 1, post + rootIndex, length - (rootIndex + 1));
return BT;
}
完整测试代码如下:
#include <iostream>
#include <stack>
using namespace std;
typedef struct BTNode
{
char data;
struct BTNode* Left;
struct BTNode* Right;
}*BTree;
BTree BuildTree_pre_in(char* pre, char* in, int length) {
if (length == 0)
return NULL;
BTree BT = new BTNode;
BT->data = *pre;
int rootIndex = 0;
//当前子树先序序列的首个结点,是当前子树的根。
while (in[rootIndex] != *pre)
rootIndex++;
//刚才找到的结点,在中序序列中,它左边的部分是它的左子树,右边的部分是它的右子树。
BT->Left = BuildTree_pre_in(pre + 1, in, rootIndex);
BT->Right = BuildTree_pre_in(pre + rootIndex + 1, in + rootIndex + 1, length - (rootIndex + 1));//因为rootIndex是下标,所以这里都要+1
return BT;
}
BTree BuildTree_in_post(char* in, char* post, int length) {
if (length == 0)
return NULL;
BTree BT = new BTNode;
BT->data = *(post + length - 1);
int rootIndex = length - 1;
//当前子树后序序列的最后一个结点,是当前子树的根。
while (in[rootIndex] != *(post + length - 1))
rootIndex--;
//刚才找到的结点,在中序序列中,它左边的部分是它的左子树,右边的部分是它的右子树。
BT->Left = BuildTree_in_post(in, post, rootIndex);
BT->Right = BuildTree_in_post(in + rootIndex + 1, post + rootIndex, length - (rootIndex + 1));
return BT;
}
void Inorder(BTree T) {
/*if (!BT)return;
Inorder(BT->Left);
cout << BT->data << " ";
Inorder(BT->Right);*/
if (!T)return;
stack<BTree>s;
while (!s.empty() || T) {
if (T) {
s.push(T);
T = T->Left;
}
else {
T = s.top(); s.pop();
cout << T->data << " ";
T = T->Right;
}
}
cout << endl;
}
void Preorder(BTree BT) {
/*if (!BT)return;
cout << BT->data << " ";
Preorder(BT->Left);
Preorder(BT->Right);*/
stack<BTree>s;
s.push(BT);
while (!s.empty()) {
BT = s.top();
s.pop();
cout << BT->data << " ";
if (BT->Right)
s.push(BT->Right);
if (BT->Left)
s.push(BT->Left);
}
cout << endl;
}
void Postorder(BTree T) {
/*if (!BT)return;
Postorder(BT->Left);
Postorder(BT->Right);
cout << BT->data << " ";*/
if (!T)return;
stack<BTree>s1, s2;
s1.push(T);
while (!s1.empty()) {
T = s1.top(); s1.pop();
s2.push(T);
if (T->Left)s1.push(T->Left);
if (T->Right)s1.push(T->Right);
}
while (!s2.empty()) {
cout << s2.top()->data << " ";
s2.pop();
}
cout << endl;
}
int main() {
char pre[] = "ABDGHCEIF";
char in[] = "GDHBAEICF";
char post[] = "GHDBIEFCA";
BTree T1 = BuildTree_pre_in(pre, in, strlen(in));
BTree T2 = BuildTree_in_post(in, post, strlen(in));
Postorder(T1);
Postorder(T2);
Preorder(T1);
Preorder(T2);
Inorder(T1);
Inorder(T2);
cout << endl;
return 0;
}
后补
二叉树的前驱后继结点,表示中序遍历时,一个结点的前一个和后一个。
获取二叉树的深度
递归
int Height(BTNode* root) {
if (!root)return 0;
return max(Height(root->Left), Height(root->Right)) + 1;
}
非递归
int Height(BTNode* root) {
queue<BTNode*>Q;
Q.push(root);
int height = 0;
while (!Q.empty()) {
int cnt = Q.size();//获取本层结点数
height++;
for (int i = 0; i < cnt; i++) {
BTNode* T = Q.front(); Q.pop();
if (T->Left)Q.push(T->Left);
if (T->Right)Q.push(T->Right);
}
}
return height;
}
判断一颗树是不是完全二叉树
bool CompleteBTree(BTNode* root) {
queue<BTNode*> Q;
bool leaf = false;
Q.push(root);
while (!Q.empty()) {
BTNode* T = Q.front();
Q.pop();
if (T->Left) {
if (leaf) return false;
Q.push(T->Left);
if (T->Right)
Q.push(T->Right);
else
//有左子树,但是没有右子树,后面所有的结点都必须是叶子结点
leaf = true;
}
else if (!T->Left && !T->Right)
//没有子树,后面所有的结点都必须是叶子结点
leaf = true;
//只有右子树,没有左子树,直接返回false
else return false;
}
return true;
}
求每个根结点的权重
int Size(BTNode *root) {
if (!root)return 0;
//懒得去改数据结构了,用data代替一下weight
return root->data = Size(root->Left) + Size(root->Right) + 1;
}



