数论篇3——扩展欧几里得算法

1、引入

最大公约数gcd算法：

辗转相除法

int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}

最小公倍数lcm算法：

根据 a*b = gcd(a,b) * lcm(a,b)

有 lcm = a*b / gcd，避免溢出，推荐写成lcm = a / gcd *b

int lcm(int a, int b) {
    return a / gcd(a, b) * b;
}

2、扩展欧几里得算法

算法定义：

算法实现

 

也就是说，我们得到了一个和gcd算法中，gcd(m,n)=gcd(n,m%n)相似，自底向上的恒等式

 

举个例子，就是

 

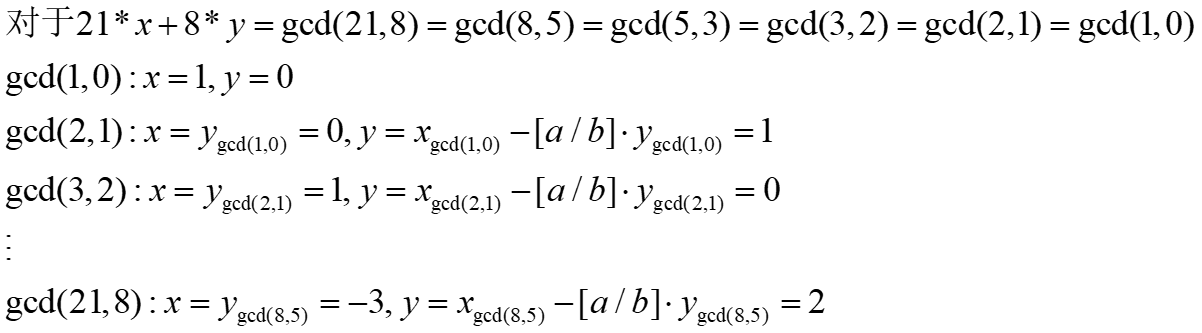
 如果想要x为正值，根据

 

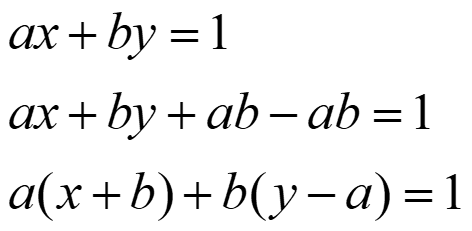
 只再做一步：

if (x < 0) {
    x += b; y -= a;
}

推广的一般情况（k为任意整数）：

$$ax+by=ax+by+\dfrac {ab}{gcd\left( a,b\right) }-\dfrac {ab}{gcd\left( a,b\right) }\\\begin{cases}x'=x+\dfrac {b}{\gcd }*k\\ y'=y-\dfrac {a}{\gcd }* k\end{cases}$$

完整代码：

int extend_gcd(int a, int b, int& x, int& y) {
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    int q = extend_gcd(b, a % b, x, y);
    int temp = x;
    x = y;
    y = temp - a / b * y;
    return q;
}

扩展：