随手练——HDU 5015 矩阵快速幂

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=5015

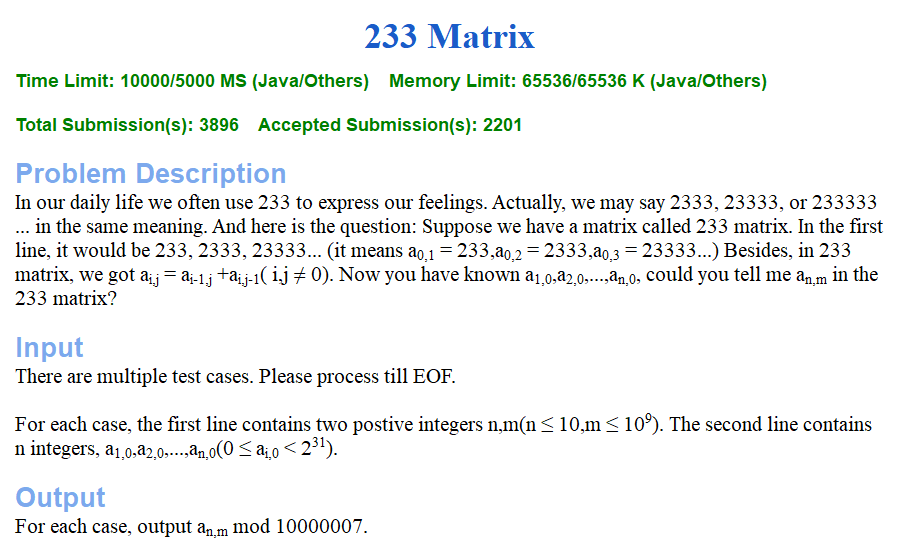
　　看到这个限时，我就知道这题不简单~~矩阵快速幂，找递推关系

 

我们假设第一列为：

23

a1

a2

a3

a4

则第二列为：

23*10+3

23*10+3+a1

23*10+3+a1+a2

23*10+3+a1+a2+a3

23*10+3+a1+a2+a3+a4

进一步转化可以得到：

代码：

#include <iostream>
#include <string.h>
using namespace std;
#define N 15
#define mod 10000007

typedef long long LL;

int n;
class Matrix{
public:
    LL mat[N][N];
    Matrix() {
        for (int i = 0; i < N; i++) {
            memset(mat[i], 0, sizeof(mat[i]));
        }
    }
    Matrix operator*(Matrix b){
        Matrix temp;
        for (int i = 0; i <= n + 1; i++){
            for (int j = 0; j <= n + 1; j++){
                for (int k = 0; k <= n + 1; k++){
                    if (mat[i][k] && b.mat[k][j]){
                        temp.mat[i][j] = (temp.mat[i][j] + (mat[i][k] % mod * b.mat[k][j] % mod) % mod) % mod;
                    }
                }
            }
        }
        return temp;
    }
};

void MatrixMulti(Matrix &M,int m){
    Matrix ans;    
    for (int i = 0; i <= n + 1; i++)
        ans.mat[i][i] = 1;
    while (m){
        if (m & 1)
            ans = ans * M;
        m >>= 1;
        M = M * M;
    }
    M = ans;
}
Matrix initialize(){
    Matrix M;
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j <= n + 1; j++) {
            if (j == 0)M.mat[i][j] = 10;
            else if (i >= j)M.mat[i][j] = 1;
            else if (j == n + 1)M.mat[i][j] = 1;
            else M.mat[i][j] = 0;
        }
    }
    M.mat[n + 1][n + 1] = 1;
    return M;
}
int main(){
    int i, m;
    while (~scanf("%d%d", &n, &m)){
        int a[N];a[0] = 23;a[n + 1] = 3;
        for (int i = 1; i <= n; i++)
            scanf("%d", &a[i]);
        Matrix M = initialize();
        MatrixMulti(M, m);
        LL res = 0;
        for (i = 0; i <= n + 1; i++)
            res = (res + (M.mat[n][i] % mod * a[i] % mod) % mod) % mod;
        cout << res << endl;
    }
    return 0;
}

 

本来是不想直接 mat[N] [N]这样直接开个大数组，时间空间上都浪费，但是这题用指针写起来真的很麻烦！！！而且不知道哪儿写错了，好一会儿我也找不到 -_-，就换成上面这个了。

#include <iostream>
#include <stdio.h>
using namespace std;

typedef long long ll;
#define mod 10000007

int** initialize(int *A,int n) {
    A[0] = 23;
    for (int i = 1; i <= n; i++) {
        cin >> A[i];
    }
    A[n + 1] = 3;
    int **M = new int*[n + 2];
    for (int i = 0; i <= n + 1; i++) {
        M[i] = new int[n + 2];
        for (int j = 0; j <= n + 1; j++) {
                if (j == 0)
                    M[i][j] = 10;
                else if (j <= i)M[i][j] = 1;
                else if (j == n + 1)M[i][j] = 1;
                else M[i][j] = 0;
        }
    }
    for (int i = 0; i <= n + 1; i++) {
        if (i == n + 1)M[n + 1][i] = 1;
        else M[n + 1][i] = 0;
    }
    return M;
}
void MatrixMulti(int **M1,int **M2,int n,int **M) {
    int t[10][10] = { 0 };
    for (int i = 0; i <= n + 1; i++) {
        for (int j = 0; j <= n + 1; j++) {
            for (int k = 0; k <= n + 1; k++) {
                t[i][j] = (t[i][j] + M1[i][k] % mod * M2[k][j] % mod) % mod;
            }
        }
    }
    for (int i = 0; i <= n + 1; i++) {
        for (int j = 0; j <= n + 1; j++) {
            M[i][j] = t[i][j];
        }
    }

}
int **getBasicMatrix(int n) {
    int **m = new int*[n + 2];
    for (int i = 0; i <= n + 1; i++) {
        m[i] = new int[n + 2];
        for (int j = 0; j <= n + 1; j++) {
            if (i == j)m[i][j] = 1;
            else m[i][j] = 0;
        }
    }
    return m;
}
int** MatrixQuickPower(int **M, int n, int m) {
    int **res = getBasicMatrix(n);
    while (m) {
        if (m & 1)
            MatrixMulti(res, M, n, res);
        MatrixMulti(M, M, n, M);
        m >>= 1;
    }
    return res;
}
int main() {
    int n, m;
    while (~scanf("%d%d", &n, &m)) {
        int res = 0; 
        int *A = new int[n + 2];
        int **M = initialize(A, n);
        M = MatrixQuickPower(M, n, m);
        for (int i = 0; i <= n + 1; i++) {
            res = (res + M[n][i] % mod * A[i] % mod) % mod;
        }
        cout << res << endl;
    }
    return 0;
}