随手练——几个递归小题目
递归最重要的两点:
1.base case(递归出口)。必须有某些基本情形,它无需递归就能解出。
2.分解 或者 分类。分解成子问题,或者每层递归分叉,也就是一个N叉树模型。
例题:
-
打印一个字符串的所有子串
分解:按顺序每个字母是否打印,分解。
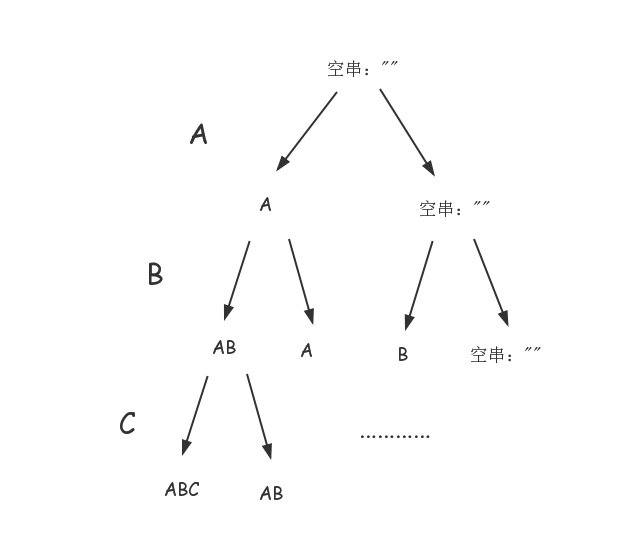
base case: 当 pos==length,分解到了最后一步
void process(char *s,int pos,int length,string res) { if (pos == length) { cout << res << endl; return; } process(s, pos + 1,length,res); process(s, pos + 1, length, res + s[pos]); } int main() { char str[] = "abc"; process(str, 0, 3,""); return 0; }
-
打印一个字符串的全排列
那里是否交换回来,都可以打印出来全排列,但是最后出来的顺序是不一样的,想要严格字典序,不换回来。
void process(string s, int n) { if (n == s.length()) { cout << s << endl; return; } for (int i = n; i < s.length(); i++) { swap(s[i], s[n]); process(s, n + 1); //swap(s[i], s[n]); } }
-
给定一个数组,数组中元素能否累加得到 指定值aim
要注意带返回值的递归函数写法:
bool recur(int *a, int n,int res,int aim,int length) { if (n == length || res == aim) { return res == aim; } return recur(a, n + 1, res + a[n], aim,length)|| recur(a, n + 1, res, aim,length); }
-
不是所有题目都适合用递归
比如:HDU 2018:http://acm.hdu.edu.cn/showproblem.php?pid=2018
两种解法,虽然递归解法要短很多,但是时间上,填表要快很多,因为递归会重复计算已经算过的值:
#include <iostream> using namespace std; int a[55]; int f(int n) { if (n <= 4) return n; return f(n - 1) + f(n - 3); } int main() { int n; a[1] = 1; a[2] = 2; a[3] = 3; a[4] = 4; for (int i = 5; i < 55; i++) { a[i] = a[i - 1] + a[i - 3]; } while (cin >> n) { if (n == 0)break; cout << a[n]<< endl; } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号