随手练——O(n)解决无序数组排序后的相邻最大差值
题目从这儿看到的 : https://mp.weixin.qq.com/s/2OXg67MfBuQjDPAJxxD8rQ,但是公众号上讲错了,问题还挺严重的。
题目知识点:桶排序。
题目:有一个无序数组2,3,1,4,6,排序后是1,2,3,4,6,最大差值是 6 - 4 = 2。
- 先找到数组的max和min。
- 创建一个长度为N+1的桶,前N个桶,(max-min)/N得到范围,左闭右开,最后一个桶只存储最大值。
- 除去第一个和最后一个,也就是N-1个数往N个桶里放,那么至少会有一个桶为空。(鸽笼原理)
- 遍历新数组Array,计算每一个非空桶中的最大值,与下一个非空桶的最小值的差,数值最大的差即为原数组排序后的相邻最大差值。(所以,每个桶只需要记录当前桶的最大值、最小值即可)
原公众号文章就是第四步错了:
举个简单的例子就知道是不对的了,最大值并不一定出现 在空桶的两侧。
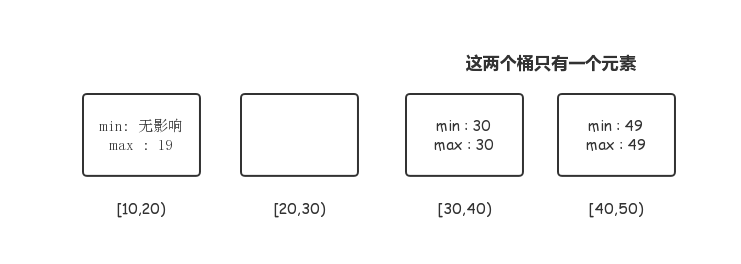
一定会有一个空桶,只能告诉我们:最大差值一定不再同一个桶里。但并不一定在空桶两侧。
代码实现:
#include "tools.h" int find_Max_Offset(int *a, int length) { int min = getMin(a, length), max = getMax(a, length); if (max == min) return 0; bool *exsit = new bool[length + 1]; memset(exsit, false, sizeof(bool)*(length + 1)); int *MAX = new int[length + 1]; int *MIN = new int[length + 1]; for (int i = 0; i < length; i++) { int index = (a[i] - min) * length / (max - min); if (!exsit[index]) { MAX[index] = MIN[index] = a[i]; exsit[index] = true; } else { MAX[index] = a[i] > MAX[index] ? a[i] : MAX[index]; MIN[index] = a[i] < MIN[index] ? a[i] : MIN[index]; } } int offset = 0; for (int i = 0; i < length;) { int max = MAX[i++]; while (exsit[i] == false) i++; int min = MIN[i]; offset = min - max > offset ? min - max : offset; } return offset; }



