BZOJ 4815 数论

今年的重庆省选？

具体就是，对于每次修改，A[p,q]这个位置，  设d=gcd(p,q) ,则 gcd为d的每一个格子都会被修改，且他们之间有个不变的联系

A[p,q]/p/q==A[k,t]/k/t   所以只要记录对于gcd为d的所有格子，只要保存A[d][d]的值就可以了。

那么求前k行k列的值ans，则所有gcd(p,q)==d的A[p,q]对答案的贡献就是    {

　　　　　　设k'=k/d;  （下取整）  f[k']*A[p,q]/(p/d)/(q/d)

}

首先有个基本结论（当n>1时）：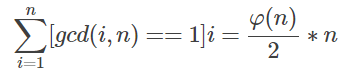

（ 若x与n互质，则n-x也与n互质 →  与n互质的数的平均数是n/2）

 

然后推得   f[n]=

代码如下：【BZOJ里最短了吧。。跑的也挺快】

 1 #include <bits/stdc++.h>
 2 #define LL long long
 3 using namespace std;
 4 const LL mo=1000000007;
 5 int S,n,m,k,t,p,q,a[4000005],f[4000005],op[10005][2];
 6 LL d,x,ans;
 7 int gcd(int x,int y){ return y?gcd(y,x%y):x;}
 8 int main(){
 9     scanf("%d%d",&m,&n); f[1]=1;
10     for (int i=2;i<=n;++i){
11         if (!a[i]) a[++t]=i,f[i]=i-1;
12         for (int j=1;j<=t;++j){
13             x=a[j]*i; if (x>n) break; a[x]=1;
14             if (!(i%a[j])) {f[x]=f[i]*a[j]; break; }else f[x]=f[i]*f[a[j]];
15         }
16     }
17     for (int i=1;i<=n;++i) f[i]=((LL)i*i%mo*f[i]+f[i-1])%mo;
18     for (int i=1;i<=m;++i){
19         scanf("%d%d%lld%d",&p,&q,&x,&k);
20         d=gcd(p,q); p/=d; q/=d;
21         op[i][0]=d; op[i][1]=(x/p/q-d*d)%mo;
22         if (op[i][1]<0) op[i][1]+=mo;
23         ans=(LL)(1+k)*k/2%mo;
24         ans=ans*ans%mo;
25         for (int j=1;j<=i;++j)
26         if (op[j][0]){
27             if (j!=i&&op[j][0]==d){ op[j][0]=0; continue;}
28             ans+=(LL)f[k/op[j][0]]*op[j][1]%mo;
29             if (ans>=mo) ans-=mo;
30         }
31         printf("%lld\n",ans);
32     }
33     return 0;
34 }
杀老师

 然后附 查了一个下午的 智障错误。。

看第21行。x/p/q-d*d， 原来这个d是不开LL的。然而 d*d可能会爆int 所以，以前一直下意识的以为只要表达式把(LL)x放最前面 后面就会自动转成LL了 。现在看来是要留个心眼了。。

posted @ 2017-05-03 21:12  cyz666  阅读(107)  评论(0)  编辑  收藏  举报