【学习笔记】一类极角排序题
总结:
- 极角排序和凸包问题有很紧密的联系。
- 通常,统计相交的计数没有统计不相交的好做。
- 为了避免精度误差,极角排序可以先判断象限,然后用叉积。
1.「日常训练」最大凸包
给出点集 \(P\),求 \(P\) 的一个子集 \(P'\),使得 \(P'\) 的所有点构成了一个凸包,并且凸包内部不包含任何其他点(不包括边界),求 \(P'\) 的最大面积为多少。\(|P| \leq 100\)。
时空限制:\(\texttt{1s/512MB}\)
枚举凸包的最低点(\(x\) 坐标最小的点,相同时取 \(y\) 最小的)作为极点,然后将极点右方的点进行极角排序。
现在有两个限制,一个限制是我们选取的点集必须构成凸包;另一个限制是凸包内不能有其他点。
对于第一个限制,考虑 \(\text{Graham}\) 扫描法的过程,就是对极角排序完的序列依次插入凸包,每次插入的时候检查当前凸包上的最后一条边是否不合法。现在每个点有选和不选两种决策。要保证选出一个点集,这个点集恰好就是凸包,当且仅当逆时针方向每两条相邻的边 \(A_kA_j,A_jA_i\) 要满足 \(\overrightarrow{A_kA_j} \times \overrightarrow{A_jA_i} > 0\)。
对于第二个限制,考虑利用我们枚举的极点 \(O\),要求这个极点 \(O\) 一定在凸包上。那么将整个凸包三角剖分,对于凸包上相邻的两个点 \(A_i,A_{i+1}\),保证 \(\triangle OA_iA_{i+1}\) 内没有点即可。
也就是说,如果我们按极角序来枚举点,我们只需要保证新加进去的点能够和最后一条边满足条件即可。因此可以考虑 DP,记 \(f(i,j)\) 表示当前凸包内最后一个点是 \(A_i\),上一个点是 \(A_j\) 的当前最大面积,那么就可以利用上面的判断条件 \(\mathcal O(n)\) 转移。总的时间复杂度为 \(\mathcal O(n^4)\)。
如果想要更给力的复杂度,可以考虑优化转移过程。考虑在转移的时候,如果我们已经求出了 \(f(i,j)\),接下来将其转移到 \(f(k,i)\),那么 \(k\) 和 \(j\) 要满足什么条件。
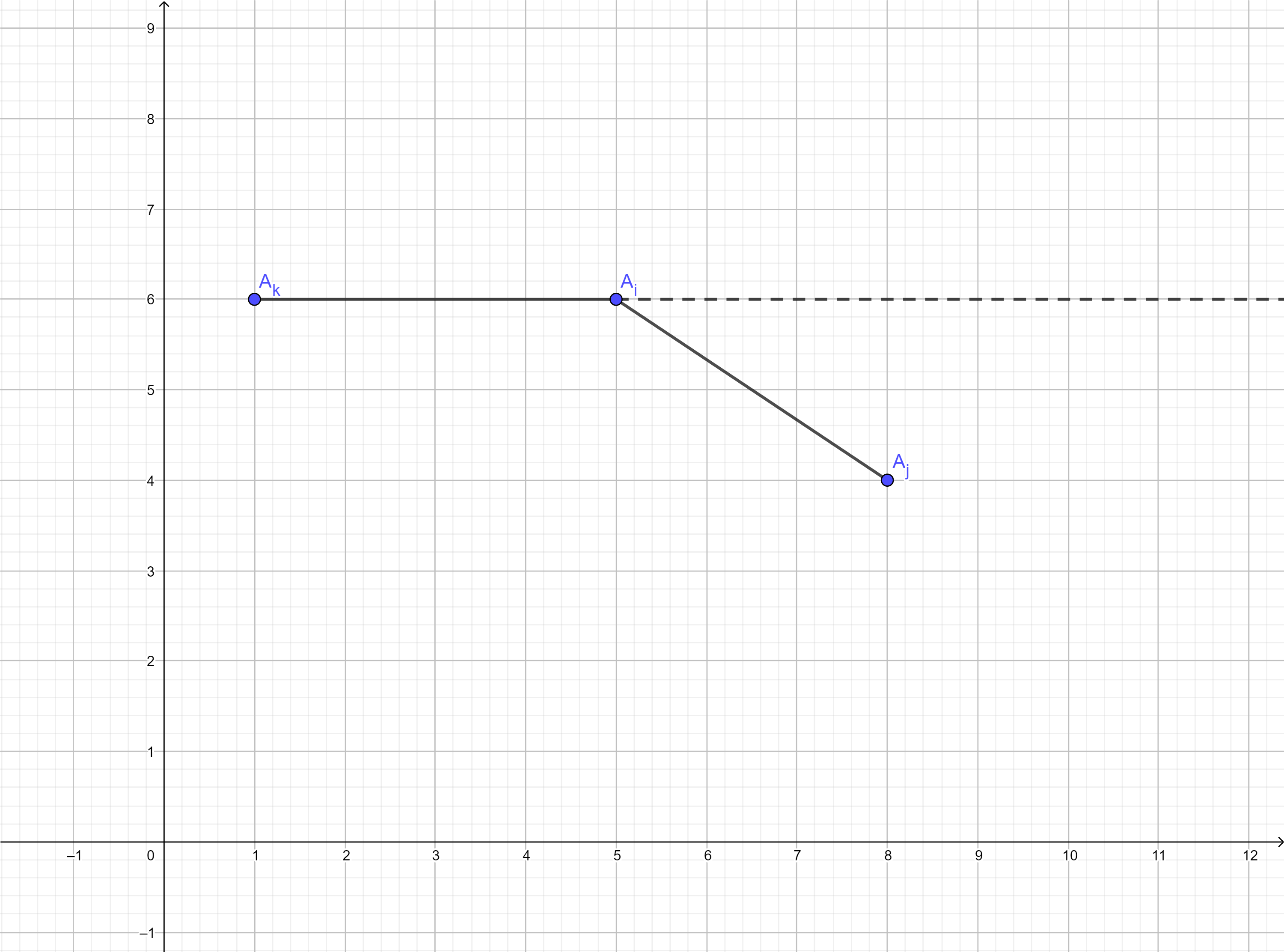
我们可以固定点 \(A_i\),将其他点极角排序,那么按极角序枚举 \(k\),用一个指针扫合法的 \(j\),必须要满足 \(\overrightarrow{A_jA_i}\times \overrightarrow{A_iA_k} > 0\)。我们就将这个部分的时间复杂度优化到了 \(\mathcal O(n^3\log n)\)。
这一题还有三角形的限制,我们可以用 bitset 存下每个线段左侧的点,优化判断过程。
代码暂时没有。
2. 「Luogu2992」三角形计数
给定一个平面内的点集,不存在两点的连线与原点相交,不存在一点与原点重合。求包含原点的三角形个数。\(n \leq 10^5\)。
时空限制:\(\texttt{1s/128MB}\)
以原点为极点极角排序。不妨尝试补集转化,转为求不包含原点的三角形个数。
枚举三角形中极角序最小的那个点 \(A\),假设它的极角为 \(\alpha\),那么极角序最大的点 \(B\) 的极角必须在 \([\alpha,\alpha+\pi)\) 之内,可以用一个指针来扫描出一个 \(B\) 能选的范围 \([l,r]\),然后这种的方案数就是在里面选两个的方案数。
最后可能需要扣除共线的情况。
代码暂时没有。
3.「CF1284E」新年和城堡建设
给定大小为 \(N\) 的点集 \(S\)。保证点集中的任意三点不共线,且不存在重复的点。
设 \(f(p)\) 表示满足如下条件的 \(S\) 的四元子集 \(T\) 的个数:
- \(T \subset S \land p \notin T\)
- \(T\) 中的元素存在一个组成四边形的方案,满足 \(p\) 在四边形内部。
请你求出的 \(\sum_{p \in S} f(p)\) 的值。\(N \leq 2500\)。
时空限制:\(\texttt{3s/1GB}\)
枚举点 \(p\),同样补集转化,求不包含它的四元子集个数。
注意到对于四个点,如果它们能构成凸四边形,那么这个凸四边形包含的点数一定是最多的。否则对于四个点,如果它们只能构成凹四边形,它们实际包含的点数(按照题目的定义)是这四个点的凸包包含的点数。
于是同样将枚举的点 \(p\) 作为极点然后夹角排序。像上面那题一样,同样先枚举一个极角最小的点,那么极角最大的点和它的跨度同样不能超过 \(\pi\),记个指针即可。扫描的时候有一些细节需要注意。时间复杂度 \(\mathcal O(n)\)。
蛮放个代码。
#include <bits/stdc++.h>
template <class T>
inline void read(T &x)
{
static char ch;
static bool opt;
while (!isdigit(ch = getchar()) && ch != '-');
x = (opt = ch == '-') ? 0 : ch - '0';
while (isdigit(ch = getchar()))
x = x * 10 + ch - '0';
if (opt)
x = ~x + 1;
}
typedef long long s64;
const int MaxN = 1e4 + 5;
struct point
{
int x, y;
point(){}
point(int _x, int _y):
x(_x), y(_y) {}
inline void scan()
{
read(x), read(y);
}
inline bool which() const
{
return y < 0 || (!y && x < 0);
}
inline void adjust()
{
if (which())
x = -x, y = -y;
}
inline point operator + (const point &rhs) const
{
return point(x + rhs.x, y + rhs.y);
}
inline point operator - (const point &rhs) const
{
return point(x - rhs.x, y - rhs.y);
}
inline s64 operator * (const point &rhs) const
{
return 1LL * x * rhs.y - 1LL * y * rhs.x;
}
inline bool operator < (const point &rhs) const
{
if (which() == rhs.which())
return *this * rhs > 0;
else
return which() < rhs.which();
}
}a[MaxN], b[MaxN];
int n, m;
inline s64 C4(int n)
{
return 1LL * n * (n - 1) * (n - 2) * (n - 3) / 24;
}
inline s64 C3(int n)
{
return 1LL * n * (n - 1) * (n - 2) / 6;
}
inline s64 C2(int n)
{
return 1LL * n * (n - 1) >> 1;
}
int main()
{
read(n);
for (int i = 1; i <= n; ++i)
a[i].scan();
s64 ans = 0;
for (int st = 1; st <= n; ++st)
{
ans += C4(n - 1);
m = 0;
for (int i = 1; i <= n; ++i)
if (st != i)
b[++m] = a[i] - a[st];
std::sort(b + 1, b + m + 1);
for (int i = 1; i <= m; ++i)
b[i + m] = b[i];
s64 res = 0;
for (int i = 1, j = 2; i <= m; ++i)
{
if (j == i - 1)
j = i;
while (j + 1 < i + m && b[i] * b[j + 1] > 0)
++j;
ans -= C3(j - i);
}
ans -= res;
}
std::cout << ans << std::endl;
return 0;
}
4.「HNOI2019」鱼
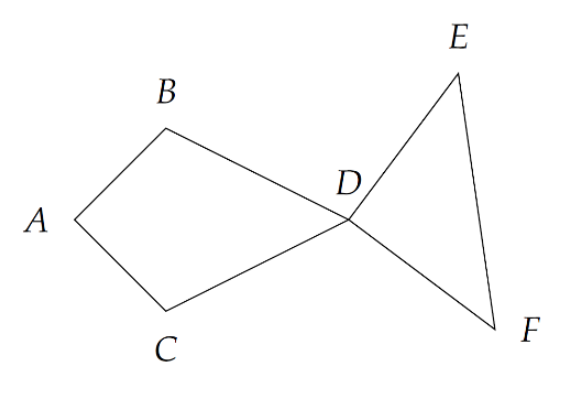
在平面坐标系上给定 \(n\) 个不同的整点(也即横坐标与纵坐标皆为整数的点)。我们称从这 \(n\) 个点中选择 \(6\) 个不同的点所组成的有序六元组 \(\langle A,B,C,D,E,F\rangle\) 是一条「鱼」,当且仅当:\(AB=AC,BD=CD,DE=DF\)(身形要对称),并且 \(\angle BAD,\angle BDA\) 与 \(\angle CAD,\angle CDA\) 都是锐角(脑袋和屁股显然不能是凹的),\(\angle ADE,\angle ADF\) 大于 \(90^\circ\)(也即为钝角或平角,为了使尾巴不至于翘那么别扭)。
下图就是一个合法的鱼的例子:
注意 \(E,F\) 都在 \(AD\) 上侧也可以是合法的。
\(n \leq 1000\)
时空限制:\(\texttt{2s/512MB}\)
不难想到枚举 \(D\) 作为极点,然后再枚举 \(A\)。那么现在 \((B,C)\) 和 \((E,F)\) 属于不同的两个区域,显然他们的选取是独立的。
\(E,F\) 必须属于一个和 \((D,A)\) 有关的半平面,同样考虑拿指针扫描,然后用哈希表(或者map啥的)来维护距离相同的点对数。
现在的主要问题是如何统计合法的点对 \((B,C)\) 的数量。我们发现,一个点对 \((B,C)\) 是合法的,当且仅当它们的连线被 \(AD\) 垂直平分,并且交点在线段 \(AD\) 上(不包括端点)。
于是我们可以将每个 \((B,C)\) 的信息表示成它们的中点和垂直于 \(BC\) 的方向向量。
那么对于每个 \((A,D)\),我们需要找的,就是和 \(AD\) 垂直(方向向量为第一关键字),并且中点在直线 \(AD\) 上(方向向量和中点的距离为第二关键字),并且中点在 \(AD\) 之间的(横纵坐标为第三关键字)。于是我们将所有 \((B,C)\) 按照上面三个关键字排序,然后查询的时候只要二分就能得到合法的 \((B,C)\) 所在区间。
坐标范围比较大,尽量避免实数运算,有些地方需要实现得比较巧妙,比如中点坐标直接用两倍存。时间复杂度 \(\mathcal O(n^2 \log n)\)。
贴个代码。
#include <bits/stdc++.h>
template <class T>
inline void read(T &x)
{
static char ch;
static bool opt;
while (!isdigit(ch = getchar()) && ch != '-');
x = (opt = ch == '-') ? 0 : ch - '0';
while (isdigit(ch = getchar()))
x = x * 10 + ch - '0';
if (opt)
x = ~x + 1;
}
typedef long long s64;
const int MaxN = 2e3 + 5;
const int MaxM = 3e6 + 5;
struct point
{
int x, y;
point(){}
point(int _x, int _y):
x(_x), y(_y) {}
inline point operator + (point rhs) const
{
return point(x + rhs.x, y + rhs.y);
}
inline point operator - (point rhs) const
{
return point(x - rhs.x, y - rhs.y);
}
inline bool operator < (point rhs) const
{
return x < rhs.x || (x == rhs.x && y < rhs.y);
}
inline bool operator != (point rhs) const
{
return x != rhs.x || y != rhs.y;
}
inline s64 operator * (point rhs) const
{
return 1LL * x * rhs.y - 1LL * y * rhs.x;
}
inline void scan()
{
read(x), read(y);
}
inline point rotate() const
{
return point(-y, x);
}
inline s64 norm() const
{
return 1LL * x * x + 1LL * y * y;
}
inline friend s64 dot(point lhs, point rhs)
{
return 1LL * lhs.x * rhs.x + 1LL * lhs.y * rhs.y;
}
inline void simplify()
{
int d = std::__gcd(abs(x), abs(y));
x /= d, y /= d;
if (x < 0 || (!x && y < 0))
x = -x, y = -y;
}
}a[MaxN];
inline bool where(point a)
{
return a.y < 0 || (a.y == 0 && a.x < 0);
}
inline bool cmp_angle(point a, point b)
{
if (where(a) != where(b))
return where(a) < where(b);
else
return a * b > 0;
}
struct seg
{
point st, dir;
seg(){}
seg(point _st, point _dir):
st(_st), dir(_dir) {dir.simplify();}
inline bool operator < (const seg &rhs) const
{
if (dir != rhs.dir)
return dir < rhs.dir;
else if (st * dir != rhs.st * dir)
return st * dir < rhs.st * dir;
else
return st < rhs.st;
}
}s[MaxM];
int n, m;
s64 cur_S;
inline int find(point a, point b)
{
if (b < a)
std::swap(a, b);
seg t1(a + a, b - a), t2(b + b, b - a);
int l = std::upper_bound(s + 1, s + m + 1, t1) - s;
int r = std::lower_bound(s + 1, s + m + 1, t2) - s;
return std::max(0, r - l);
}
int main()
{
#ifdef orzczk
freopen("fish.in", "r", stdin);
freopen("fish.out", "w", stdout);
#endif
read(n);
for (int i = 1; i <= n; ++i)
a[i].scan();
for (int i = 1; i < n; ++i)
for (int j = i + 1; j <= n; ++j)
s[++m] = seg(a[i] + a[j], (a[j] - a[i]).rotate());
std::sort(s + 1, s + m + 1);
s64 ans = 0;
for (int D = 1; D <= n; ++D)
{
int cnt = 0;
static point b[MaxN];
for (int i = 1; i <= n; ++i)
if (i != D)
b[++cnt] = point(a[i] - a[D]);
std::sort(b + 1, b + cnt + 1, cmp_angle);
for (int i = 1; i <= cnt; ++i)
b[cnt + i] = b[i];
std::map<s64, int> S;
S.clear(); cur_S = 0;
int l = 1, r = 1; //[l, r)
for (int A = 1; A <= cnt; ++A)
{
while (b[A] * b[r] > 0 || (b[A] * b[r] == 0 && r <= cnt) || dot(b[A], b[r]) < 0)
cur_S += S[b[r++].norm()]++;
while (l < r && dot(b[l], b[A]) >= 0)
cur_S -= --S[b[l++].norm()];
if (cur_S)
ans += 1LL * cur_S * find(a[D], a[D] + b[A]);
}
}
std::cout << (ans << 2) << '\n';
return 0;
}
5.「JOISC 2014 Day4」两个人的星座
平面内有 \(n\) 个点,有三种颜色,每个点的颜色是三种中的一种。求没有公共点且不是包含关系的三色三角形对数。
\(n \leq 3000\)
时空限制:\(\texttt{9s/512MB}\)
首先拿到这题可能是毫无头绪的。需要找到突破口,我们发现还是不相交的情况比较好计数。
考虑到两个相离的三角形必然有两条内公切线。
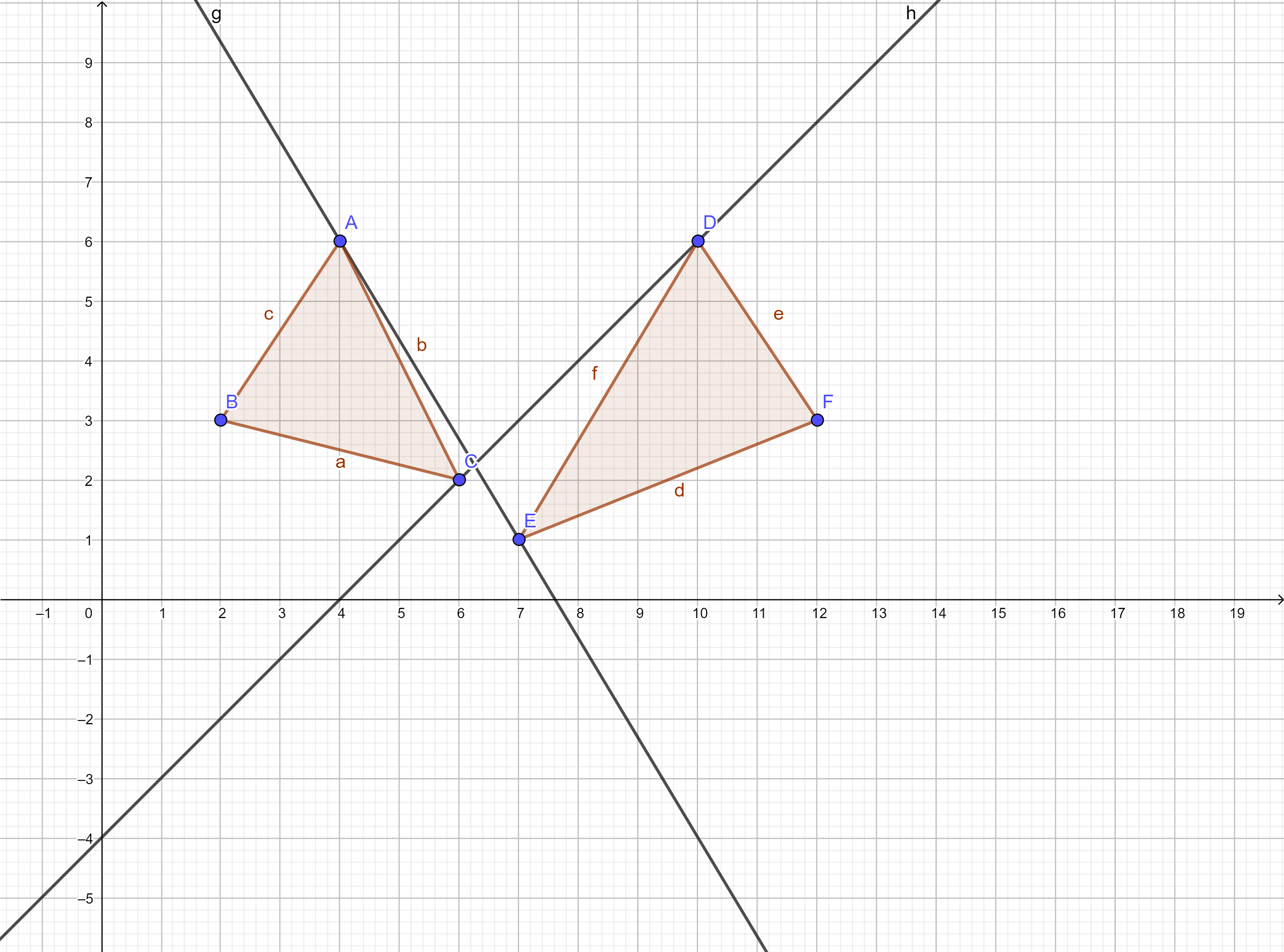
那么枚举其中内公切线一个端点作为极点,其他点极角排序,然后枚举另外一个点作为内公切线的另一个端点。
那么两个三角形就要分属两侧,我们记两个数组表示两侧每种颜色的点数有多少个,然后根据这两个点的颜色计数即可。会被重复计数 \(4\) 次,最后除一下就行。时间复杂度 \(\mathcal O(n^2\log n)\)。
贴个代码。
#include <bits/stdc++.h>
template <class T>
inline void read(T &x)
{
static char ch;
static bool opt;
while (!isdigit(ch = getchar()) && ch != '-');
x = (opt = ch == '-') ? 0 : ch - '0';
while (isdigit(ch = getchar()))
x = x * 10 + ch - '0';
if (opt)
x = ~x + 1;
}
typedef long long s64;
const int MaxN = 1e4 + 5;
struct point
{
int x, y, c;
point(){}
point(int _x, int _y, int _c = 0):
x(_x), y(_y), c(_c) {}
inline void scan()
{
read(x), read(y), read(c);
}
inline bool which() const
{
return y < 0 || (!y && x < 0);
}
inline point operator + (point rhs) const
{
return point(x + rhs.x, y + rhs.y);
}
inline point operator - (point rhs) const
{
return point(x - rhs.x, y - rhs.y, c);
}
inline s64 operator * (point rhs) const
{
return 1LL * x * rhs.y - 1LL * y * rhs.x;
}
inline bool operator < (const point &rhs) const
{
if (which() != rhs.which())
return which() < rhs.which();
else
return *this * rhs > 0;
}
}a[MaxN];
int n, m;
s64 ans;
int main()
{
read(n);
for (int i = 1; i <= n; ++i)
a[i].scan();
for (int st = 1; st <= n; ++st)
{
static point b[MaxN];
static int cnt[2][3];
m = 0;
memset(cnt, 0, sizeof(cnt));
for (int i = 1; i <= n; ++i)
if (i != st)
{
b[++m] = a[i] - a[st];
++cnt[0][b[m].c];
}
std::sort(b + 1, b + m + 1);
for (int i = 1; i <= m; ++i)
b[i + m] = b[i];
for (int i = 1, j = 1; i <= m; ++i)
{
if (j == i)
{
--cnt[0][b[j].c];
++cnt[1][b[j].c];
++j;
}
while (j < i + m && b[i] * b[j] > 0)
{
--cnt[0][b[j].c];
++cnt[1][b[j].c];
++j;
}
--cnt[1][b[i].c];
s64 cur1 = 1, cur2 = 1;
for (int k = 0; k < 3; ++k)
{
if (k != a[st].c)
cur1 *= cnt[0][k], cur2 *= cnt[1][k];
if (k != b[i].c)
cur1 *= cnt[1][k], cur2 *= cnt[0][k];
}
ans += cur1 + cur2;
++cnt[0][b[i].c];
}
}
std::cout << (ans >> 2) << std::endl;
return 0;
}
6. 「日常训练」踢罐子
给定平面上的 \(n\) 个整点,不存在两点重合、三点共线。
现在等概率地选取一点 \(A\),再从剩下 \(n-1\) 个点中等概率地选取一个点 \(B\),再从剩下 \(n-2\) 个点中等概率地选取一个点 \(C\)。接下来计算 \((A,B,C)\) 这种选取方案的权值。
作 \(A,B,C\) 的外接圆,考虑 \(n\) 个点的出现位置。对于弧 \(BC\) 上的点(包括 \(B,C\)),每个点贡献 $\frac 1 2 $ 的权值;对于弧 \(BC\) 和线段 \(BC\) 之间的点(不包括边界),每个点贡献 \(1\) 的权值;特别地,\(A\) 点贡献 \(1\) 的权值。
\(3 \leq n \leq 1000\)
先把 \(ABC\) 三点的贡献额外处理,即 \(2\times 2n(n-1)(n-2)\)。
发现 \(D\) 在 \(ABC\)(\(A\) 和 \(D\) 相对)的外接圆弧和弦之间当且仅当,\(ABCD\) 构成凸四边形且 \(A+D\geq π\)。特殊的当 \(A+D=π\) 时四点共圆,任选其中三点,另外一个点一定在弧上,对答案总贡献 \(4\)。
否则 \(A+D>π,B+C<π\),那么 \(A\) 和 \(D\) 分别剩下三个点的外接圆的弧和弦之间,\(B\) 和 \(C\) 则不在,因此对答案贡献也是 \(4\)。
因此问题转化为统计凸四边形个数(非凸四边形任取三点都无贡献)。考虑一个四边形四个顶点两两连边,凸四边形有四种情况剩下两个点在同侧,两种情况在异侧;非凸四边形则分别有三种情况。
因此设有 \(a\) 个凸四边形,\(b\) 个非凸四边形,枚举点对统计多少剩下两点在异侧/同侧方案数,记作 \(X,Y\),则 \(2a+3b=X,4a+3b=Y\),所以 \(a=\frac{Y-X}{2}\),最后答案是 \(4a\)。
现在的问题就是如何枚举点对,计算出同侧异侧的点对数。
我们可以枚举点对的其中一个点,将其他点按极角排序,然后扫描一遍就能顺便维护出这个信息了。时间复杂度 \(O(n^2\log n)\)。
贴个程序(题比较早以前写的,极角排序写得比较 naive)
#include <bits/stdc++.h>
const int MaxN = 2e3 + 5;
const double pi = acos(-1.0);
typedef long long s64;
struct point
{
double x, y;
point(){} point(double a, double b): x(a), y(b) {}
inline void scan()
{
scanf("%lf%lf", &x, &y);
}
inline double slope()
{
return atan2(y, x);
}
inline point operator - (const point &rhs) const
{
return point(x - rhs.x, y - rhs.y);
}
}p[MaxN];
int n;
s64 ans;
double a[MaxN];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
p[i].scan();
ans = 4LL * n * (n - 1) * (n - 2);
if (n == 3)
{
std::cout << ans << std::endl;
return 0;
}
int tot;
for (int st = 1; st <= n; ++st)
{
tot = 0;
for (int i = 1; i <= n; ++i)
{
if (i == st) continue;
a[++tot] = (p[i] - p[st]).slope();
if (a[tot] < 0) a[tot] += 2 * pi;
if (a[tot] > 2 * pi) a[tot] -= 2 * pi;
a[++tot] = a[tot - 1] + 2 * pi;
}
std::sort(a + 1, a + tot + 1);
int r = 1;
for (int i = 1; i < n; ++i)
{
for (; r < tot && a[r + 1] <= a[i] + pi; ++r);
int lef = r - i;
int rit = n - 2 - lef;
s64 X = (1LL * lef * (lef - 1) + 1LL * rit * (rit - 1)) >> 1;
s64 Y = 1LL * lef * rit;
ans += 2 * (X - Y);
}
}
std::cout << ans << std::endl;
return 0;
}
7. 「COCI 2021.3」Geometrija
给定平面内 \(n\) 个整点,不存在三点共线,统计有多少线段与其他线段都不相交(两个线段相交,当且仅当二者存在一个端点之外的公共点)。\(n \leq 1000\),坐标绝对值 \(\leq 10^9\)。
好久之后又碰到了这种题,结果发现自己竟然想不到反过来做。
一个线段和其他线段都不相交,直观的想法是判断是否存在一个线段和它相交,但是统计和它不相交的线段数会好做很多。如果和它不相交的线段数等于 \(\dbinom {n - 2} 2\),就意味着这个线段合法。
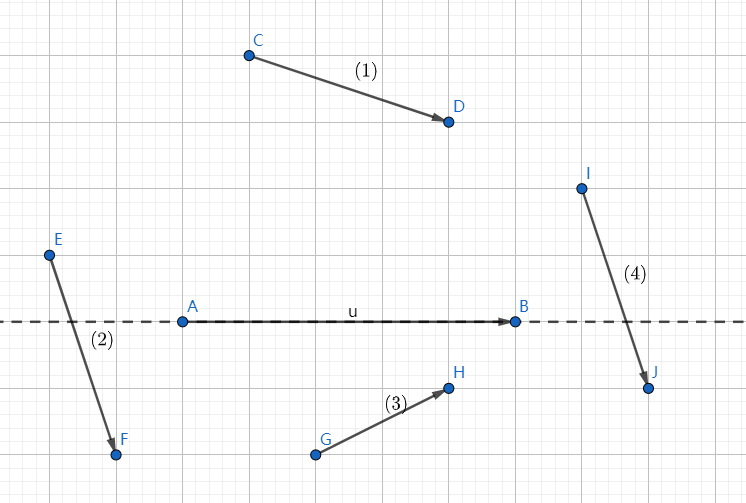
对于线段 \(\overline{AB}\),有上图四类不相交的线段,\((3)(4)\) 和 \((1)(2)\) 是对称的,可以类似统计。
\((1)\) 相当好数,只需要枚举 \(A\) 然后以 \(A\) 为极点将其他点极角排序,然后扫一遍,用指针维护 \(\vec{AB}\) 上侧的点数即可。
\((2)\) 就做一些转化,将下侧的点翻到上侧。具体地来说就是把每个点关于 \(A\) 中心对称点都找出来一起极角排序(这样你甚至不需要存指针,排序后 \(B\) 和 \(B'\) 之间的点就是 \(\vec{AB}\) 上侧的),然后统计一下 翻转点 极角序在 未反转点 之前的点对数即可(因为只会在头尾增减,所以很容易维护)。
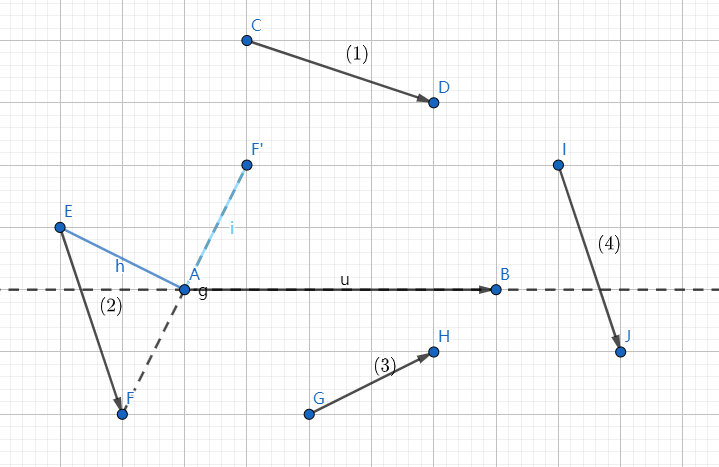
时间复杂度 \(\mathcal O(n^2 \log n)\)。
#include <bits/stdc++.h>
using namespace std;
typedef long long s64;
struct point {
int x, y;
point(){}
point(int xa, int xb): x(xa), y(xb) {}
inline point operator - (const point &rhs) const {
return point(x - rhs.x, y - rhs.y);
}
inline s64 operator * (const point &rhs) const {
return 1LL * x * rhs.y - 1LL * y * rhs.x;
}
inline int side() const {
if (y > 0 || (y == 0 && x > 0)) {
return 0;
} else {
return 1;
}
}
inline bool operator < (const point &rhs) const {
if (side() != rhs.side())
return side() < rhs.side();
else
return *this * rhs > 0;
}
};
const int MaxN = 1000 + 5;
int n;
point a[MaxN];
struct node {point p; int opt, pos;};
vector<node> p[MaxN];
int sze;
int ans[MaxN][MaxN];
int C2(int x) {
return x * (x - 1) / 2;
}
void solve(int S) {
vector<node> &V = p[S];
int cnt[2] = {0};
auto nxt = [&](int x) {
return ++x == sze ? 0 : x;
};
++cnt[V[0].opt];
for (int i = 0, j = 0, cp = 0; i < sze; ++i) {
while (nxt(j) != i && V[i].p * V[nxt(j)].p > 0) {
j = nxt(j);
if (V[j].opt == 0) cp += cnt[1];
++cnt[V[j].opt];
}
if (V[i].opt == 1) cp -= cnt[0];
--cnt[V[i].opt];
if (V[i].opt == 0)
ans[S][V[i].pos] = C2(cnt[0]) + cp;
}
}
int main() {
#ifdef orzczk
freopen("c.in", "r", stdin);
freopen("c.out", "w", stdout);
#endif
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d%d", &a[i].x, &a[i].y);
}
sze = (n - 1) << 1;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j)
if (i != j) {
p[i].push_back({a[j] - a[i], 0, j});
p[i].push_back({a[i] - a[j], 1, j});
}
sort(p[i].begin(), p[i].end(), [&](node pa, node pb) {
return pa.p < pb.p;
});
}
for (int i = 1; i <= n; ++i) {
solve(i);
}
int ansCount = 0;
for (int i = 1; i < n; ++i)
for (int j = i + 1; j <= n; ++j) {
// cerr << i << ' ' << j << ' ' << ans[i][j] << ' ' << ans[j][i] << ' ' << C2(n - 2) - ans[i][j] - ans[j][i] << '\n'; //
ansCount += ans[i][j] + ans[j][i] == C2(n - 2);
}
cout << ansCount << '\n';
return 0;
}