实验3 C语言函数应用编程

问题1：
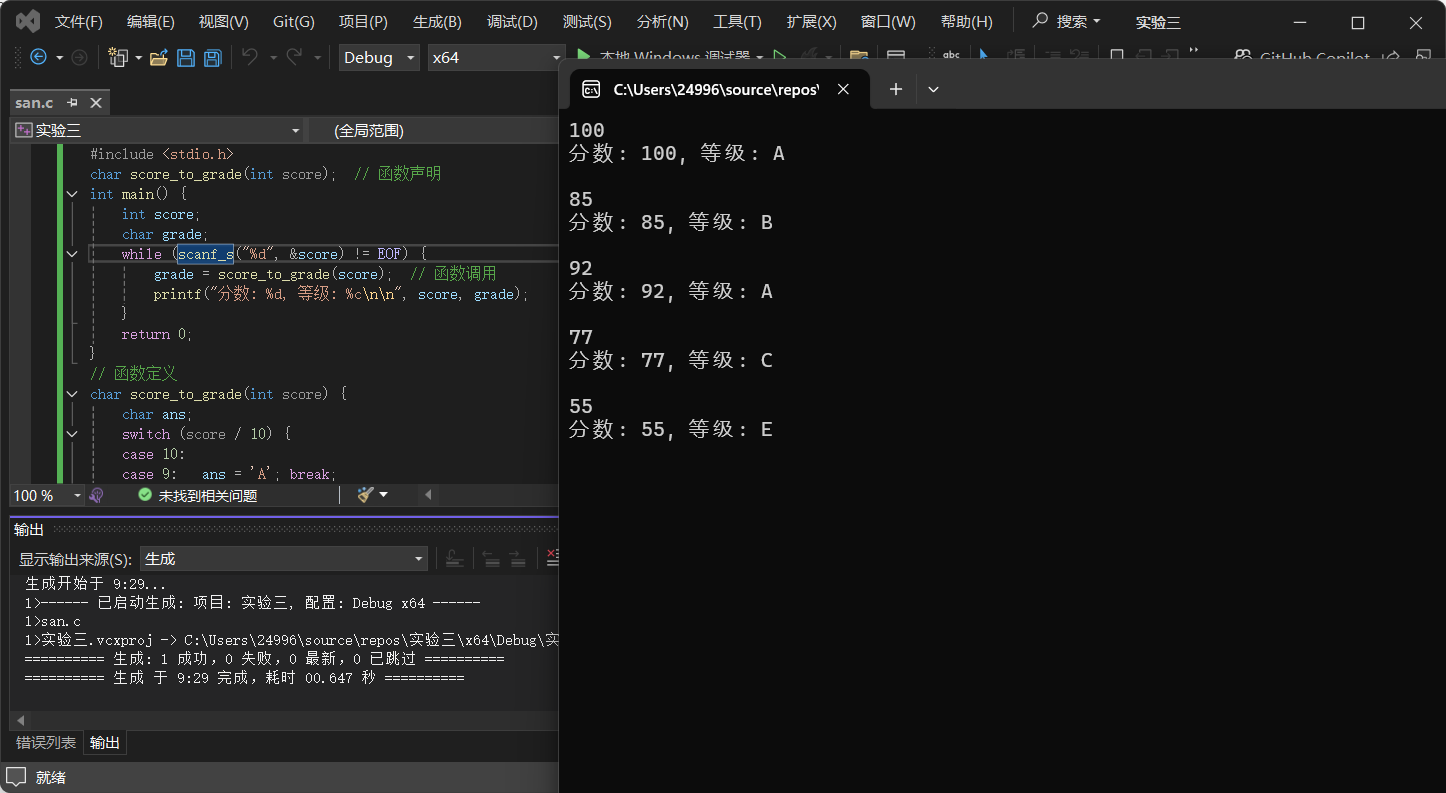
函数score_to_grade的功能是将输入的整数分数（0-100）转换为对应的等级（A-E）。形参类型是int，返回值类型是char。

问题2：
修改后的switch代码存在以下问题：1.缺少break语句：每个case分支后未使用break，导致控制流穿透。例如，当分数为90时，会依次执行case 9到default的所有分支，最终结果错误。2.类型不匹配：case分支中使用双引号"A"表示字符串，而ans是char类型，应使用单引号'A'。双引号会导致编译错误

问题1：
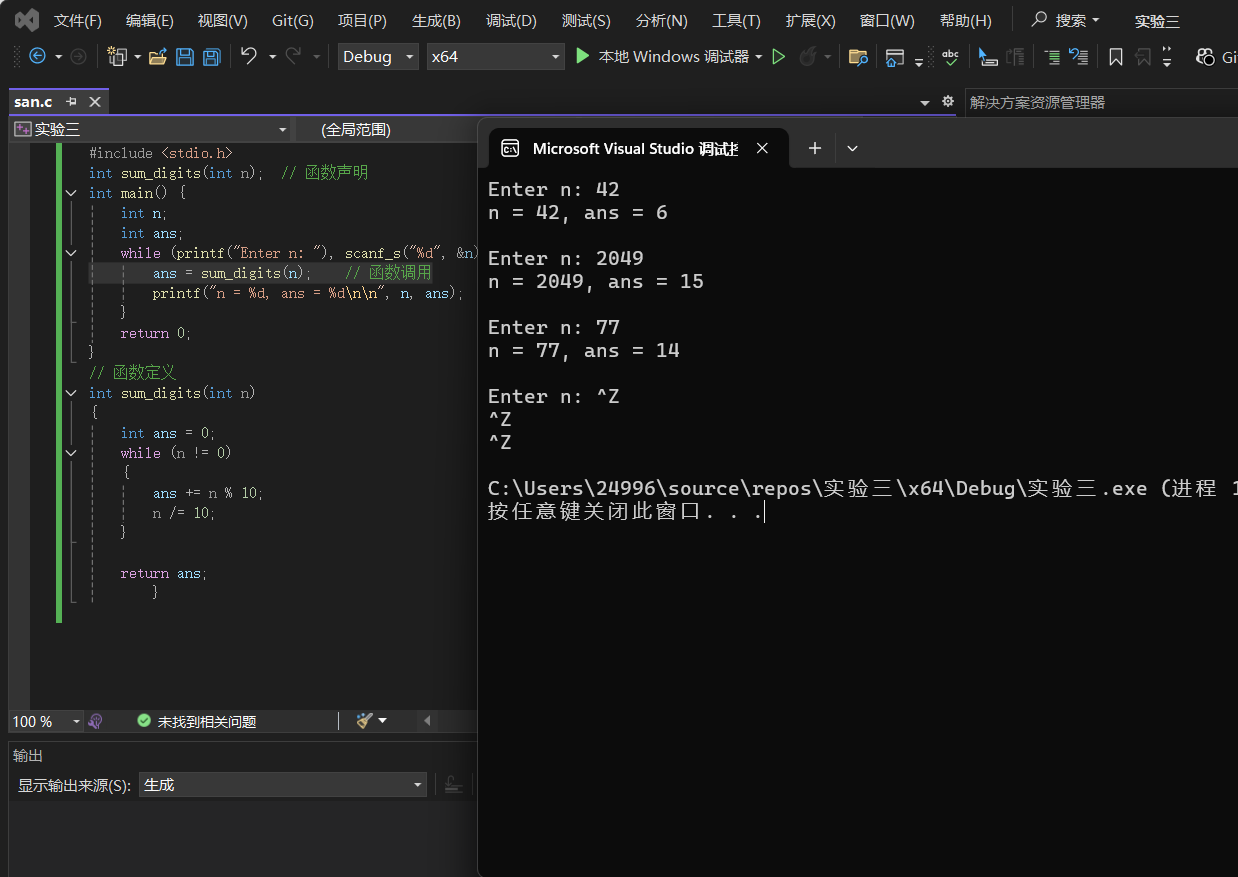
函数sum_digits的功能是计算整数n的各位数字之和。例如，输入42时，计算4 + 2 = 6；输入2049时，计算2 + 0 + 4 + 9 = 15。

问题2：
如果将函数sum_digits改为递归实现，可以实现同等效果。两种实现方式的算法思维区别如下：

原函数（迭代）：

算法思维：通过循环逐次取n的个位数字（n % 10），累加到结果中，然后通过n /= 10去掉已处理的个位，直到n变为0。

特点：显式使用循环控制流程，逐步处理每一位，是典型的迭代思维。

递归版本：

算法思维：将问题分解为更小的子问题。每次递归处理去掉个位后的剩余数字（n / 10），并将当前个位（n % 10）与子问题的结果相加。

特点：通过函数自身的递归调用隐式分解问题，最终通过基线条件（n < 10）终止递归，是分治思想的体现。

问题一：

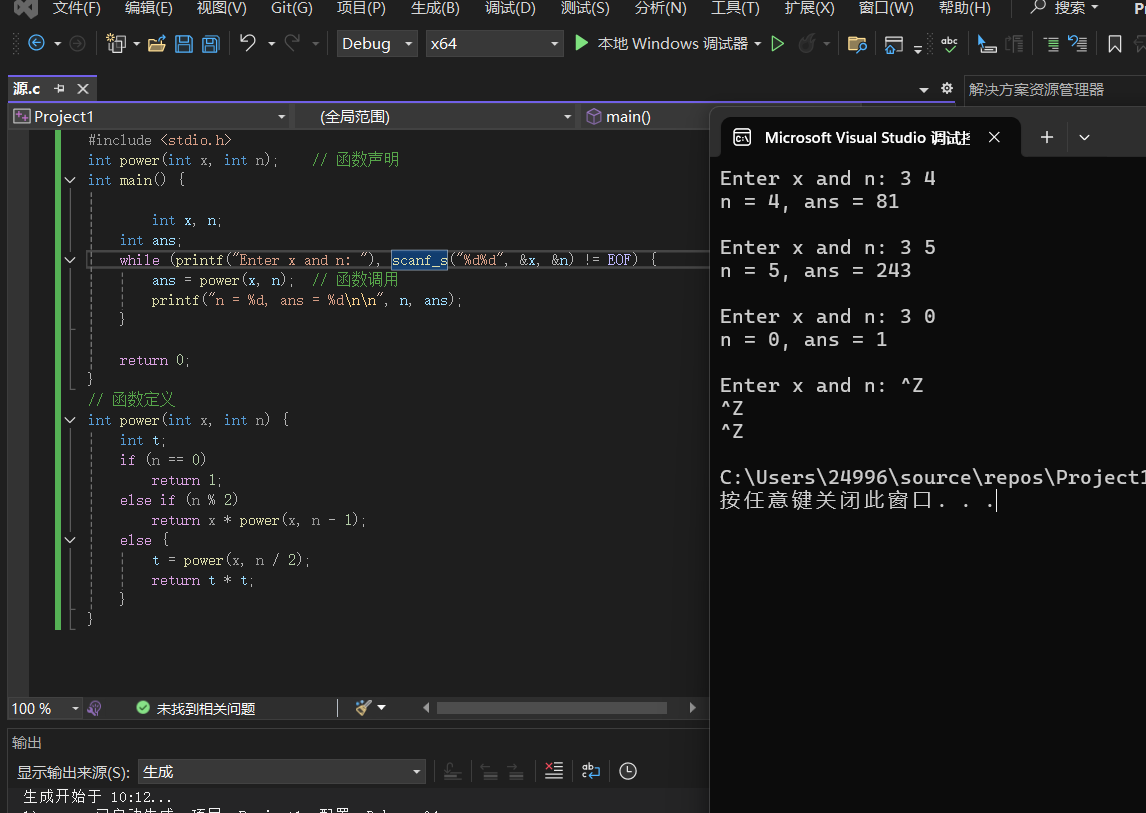
函数 power 的功能是计算整数 x 的 n 次幂（即 x^n）。它通过递归的方式实现了幂运算，并针对 n 的奇偶性进行了优化：

如果 n 是 0，直接返回 1（因为任何数的 0 次幂都是 1）。
如果 n 是奇数，递归计算 x * power(x, n - 1)。
如果 n 是偶数，递归计算 power(x, n / 2) 的平方（即 t * t）。

这种分治策略将问题规模不断减半，使得时间复杂度从朴素递归的 O(n) 优化到 O(log n)。

问题二：

是的，函数 power 是一个递归函数。它的递归模式如下：

基本情况（Base Case）：当 n == 0 时，power(x, n) = 1。
递归情况（Recursive Cases）：1.如果 n 是奇数（即 n % 2 != 0），则：
如果 n 是偶数（即 n % 2 == 0），则: $power(x,n)=power(x,n/2)^2$
对于奇数 n，先计算 x^(n-1)（递归），然后乘以 x。对于偶数 n，先计算 x^(n/2)（递归），然后平方结果。
- 这种分治策略避免了重复计算，显著提高了效率。例如：
  - 计算 3^4：
    - 3^4 = (3^2)^2 = 9^2 = 81。
  - 计算 3^5：
    - 3^5 = 3 * 3^4 = 3 * 81 = 243。

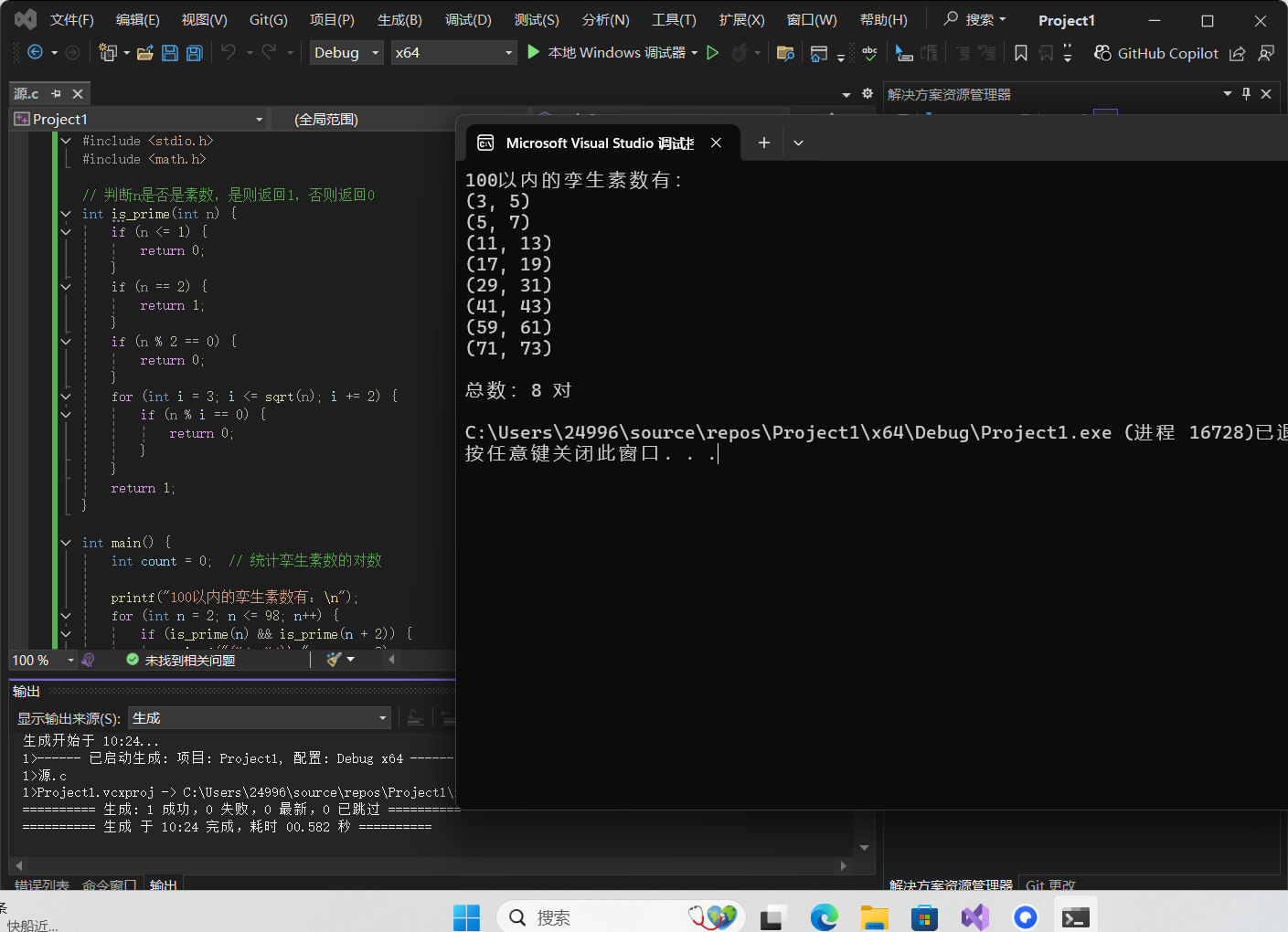
#include <stdio.h>
#include <math.h>

// 判断n是否是素数，是则返回1，否则返回0
int is_prime(int n) {
    if (n <= 1) {
        return 0;
    }
    if (n == 2) {
        return 1;
    }
    if (n % 2 == 0) {
        return 0;
    }
    for (int i = 3; i <= sqrt(n); i += 2) {
        if (n % i == 0) {
            return 0;
        }
    }
    return 1;
}

int main() {
    int count = 0;  // 统计孪生素数的对数

    printf("100以内的孪生素数有：\n");
    for (int n = 2; n <= 98; n++) {
        if (is_prime(n) && is_prime(n + 2)) {
            printf("(%d, %d)\n", n, n + 2);
            count++;
        }
    }

    printf("\n总数：%d 对\n", count);
    return 0;
}

#include <stdio.h>

// 全局变量：记录移动次数
int move_count = 0;

// Hanoi 塔递归函数
void hanoi(int n, char from, char to, char aux) {
if (n == 1) {
printf("Move disk 1 from %c to %c\n", from, to);
move_count++;
return;
}
hanoi(n - 1, from, aux, to);
printf("Move disk %d from %c to %c\n", n, from, to);
move_count++;
hanoi(n - 1, aux, to, from);
}

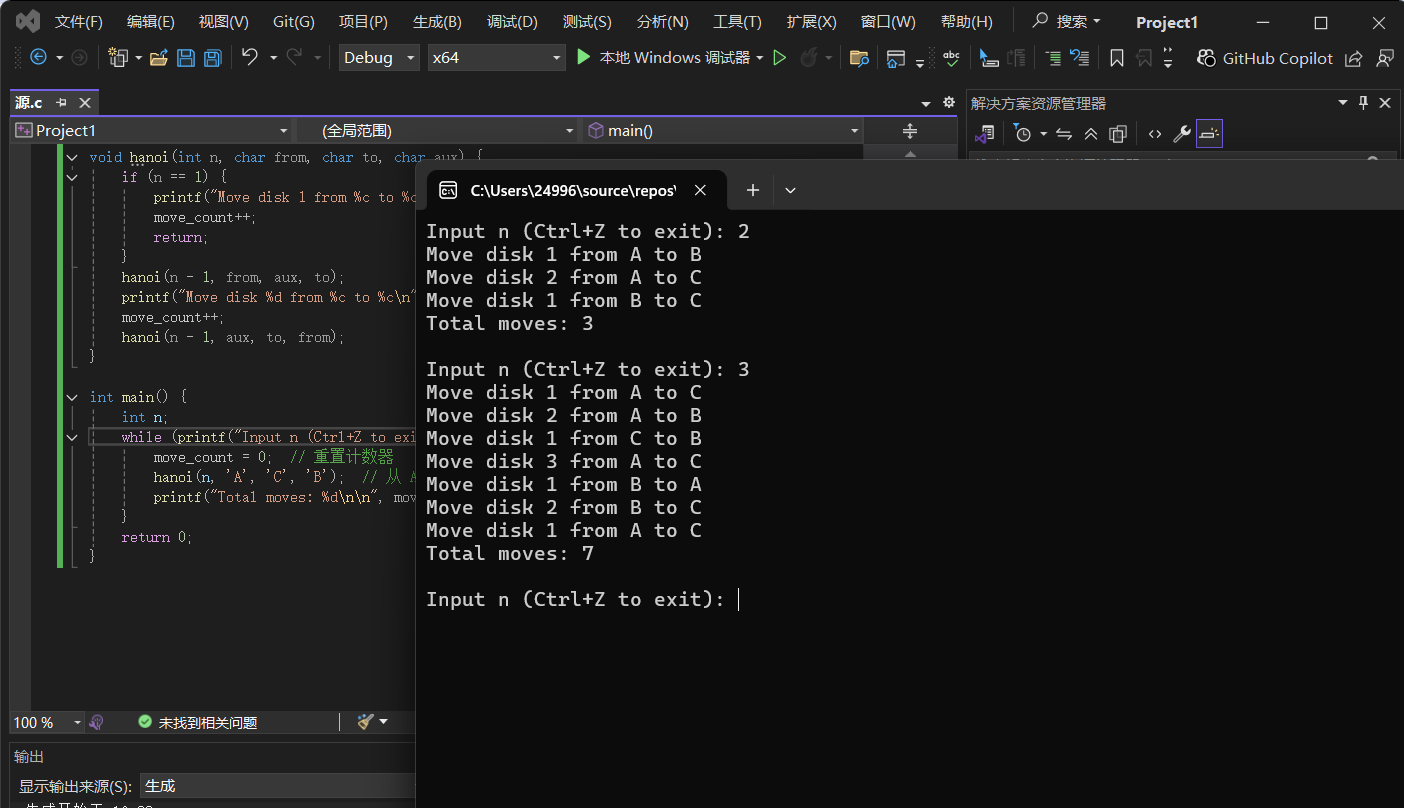
int main() {
int n;
while (printf("Input n (Ctrl+Z to exit): "), scanf_s("%d", &n) != EOF) {
move_count = 0; // 重置计数器
hanoi(n, 'A', 'C', 'B'); // 从 A 移动到 C，借助 B
printf("Total moves: %d\n\n", move_count);
}
return 0;
}

#include <stdio.h>

// 方法1：迭代方式计算组合数
int func_iterative(int n, int m) {
if (m < 0 || m > n) {
return 0; // 非法输入
}
if (m == 0 || m == n) {
return 1;
}
// 优化计算方式，避免阶乘溢出
long long res = 1;
for (int i = 1; i <= m; i++) {
res = res * (n - m + i) / i;
}
return (int)res;
}

// 方法2：递归方式计算组合数
int func_recursive(int n, int m) {
if (m < 0 || m > n) {
return 0; // 非法输入
}
if (m == 0 || m == n) {
return 1;
}
return func_recursive(n - 1, m - 1) + func_recursive(n - 1, m);
}

// 主函数（题目已给出）
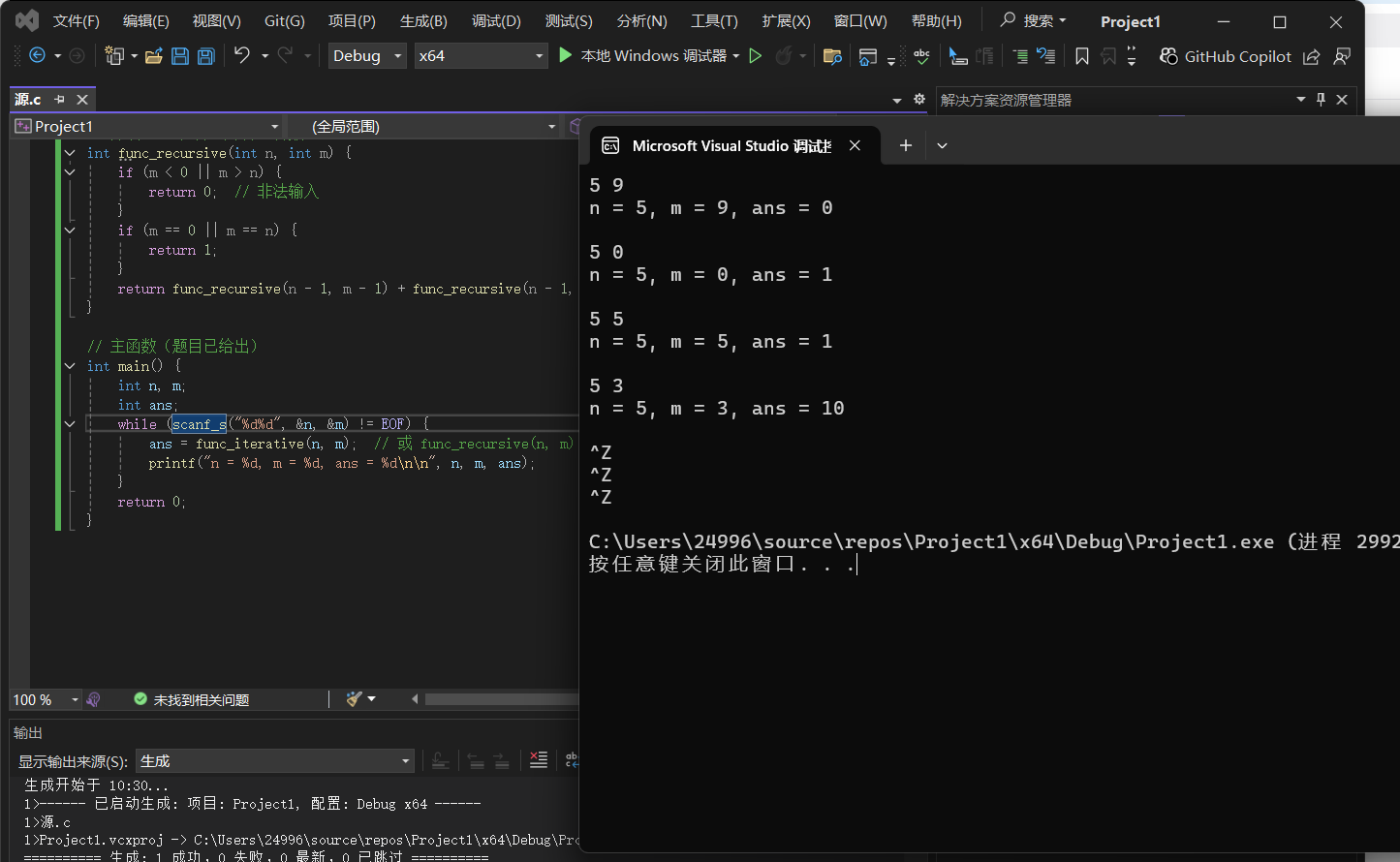
int main() {
int n, m;
int ans;
while (scanf_s("%d%d", &n, &m) != EOF) {
ans = func_iterative(n, m); // 或 func_recursive(n, m)
printf("n = %d, m = %d, ans = %d\n\n", n, m, ans);
}
return 0;
}

#include <stdio.h>

// 函数定义：计算三个数的最大公约数（穷举法）
int gcd(int a, int b, int c) {
int min = a; // 先假设 a 是最小的
if (b < min) min = b;
if (c < min) min = c;

// 从 min 开始递减检查
for (int i = min; i >= 1; i--) {
if (a % i == 0 && b % i == 0 && c % i == 0) {
return i; // 找到最大公约数
}
}
return 1; // 所有数至少公约数为 1
}

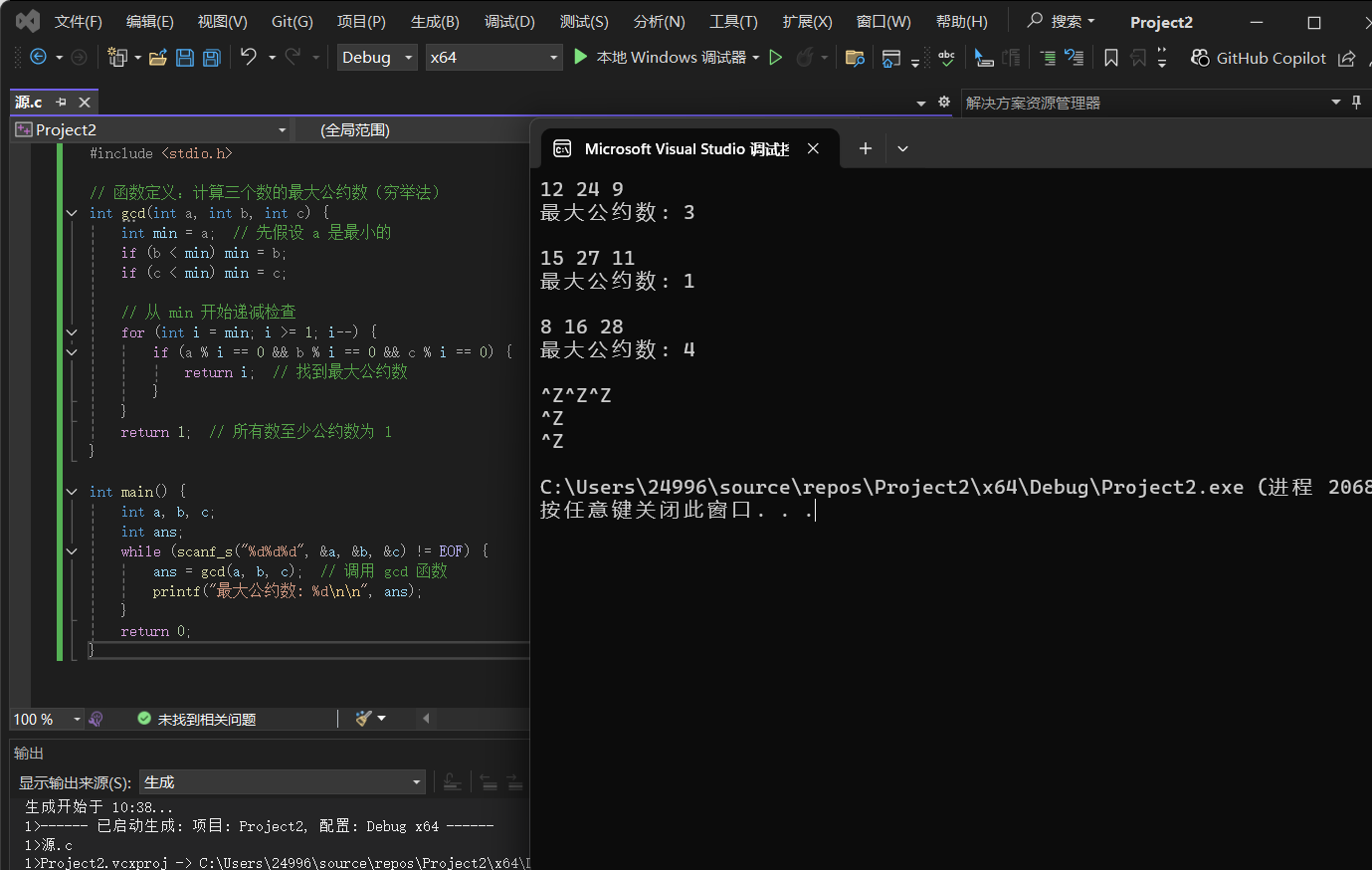
int main() {
int a, b, c;
int ans;
while (scanf_s("%d%d%d", &a, &b, &c) != EOF) {
ans = gcd(a, b, c); // 调用 gcd 函数
printf("最大公约数: %d\n\n", ans);
}
return 0;
}

posted @ 2025-04-07 10:39 awfasf 阅读(5) 评论(0) 收藏举报

刷新页面返回顶部

实验3 C语言函数应用编程

公告