洛谷P2597 [ZJOI2012] 灾难 [拓扑排序，LCA]

　　题目传送门

灾难

 

题目描述

 

阿米巴是小强的好朋友。

 

阿米巴和小强在草原上捉蚂蚱。小强突然想，如果蚂蚱被他们捉灭绝了，那么吃蚂蚱的小鸟就会饿死，而捕食小鸟的猛禽也会跟着灭绝，从而引发一系列的生态灾难。

 

学过生物的阿米巴告诉小强，草原是一个极其稳定的生态系统。如果蚂蚱灭绝了，小鸟照样可以吃别的虫子，所以一个物种的灭绝并不一定会引发重大的灾难。

 

我们现在从专业一点的角度来看这个问题。我们用一种叫做食物网的有向图来描述生物之间的关系：

 

一个食物网有N个点，代表N种生物，如果生物x可以吃生物y，那么从y向x连一个有向边。

 

这个图没有环。

 

图中有一些点没有连出边，这些点代表的生物都是生产者，可以通过光合作用来生存； 而有连出边的点代表的都是消费者，它们必须通过吃其他生物来生存。

 

如果某个消费者的所有食物都灭绝了，它会跟着灭绝。

 

我们定义一个生物在食物网中的“灾难值”为，如果它突然灭绝，那么会跟着一起灭绝的生物的种数。

 

举个例子：在一个草场上，生物之间的关系是：

 

如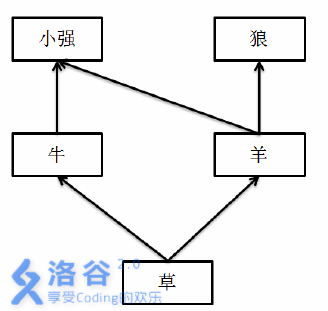 

 

如果小强和阿米巴把草原上所有的羊都给吓死了，那么狼会因为没有食物而灭绝，而小强和阿米巴可以通过吃牛、牛可以通过吃草来生存下去。所以，羊的灾难值是1。但是，如果草突然灭绝，那么整个草原上的5种生物都无法幸免，所以，草的灾难值是4。

 

给定一个食物网，你要求出每个生物的灾难值。

 

输入输出格式

输入格式：

 

 

输入文件 catas.in 的第一行是一个正整数 N，表示生物的种数。生物从 1 标

 

号到 N。

 

接下来 N 行，每行描述了一个生物可以吃的其他生物的列表，格式为用空

 

格隔开的若干个数字，每个数字表示一种生物的标号，最后一个数字是 0 表示列

 

表的结束。

 

 

输出格式：

 

 

输出文件catas.out包含N行，每行一个整数，表示每个生物的灾难值。

 

 

 

输入输出样例

 

输入样例#1： 

5
0
1 0
1 0
2 3 0
2 0

输出样例#1： 

4
1
0
0
0

 

说明

 

【样例说明】

 

样例输入描述了题目描述中举的例子。

 

【数据规模】

 

对50%的数据，N ≤ 10000。

 

对100%的数据，1 ≤ N ≤ 65534。

 

输入文件的大小不超过1M。保证输入的食物网没有环。

---

　　分析：

　　看懂题意后很自然朝着拓扑排序的方向想，那么在拓扑的过程中我们怎么记录节点对答案的贡献呢？

　　实际上这道题在拓扑排序的过程中是没办法记录节点对答案的贡献的，那么就换一种思路，在拓扑排序过程中我们把这张图重建成一棵树，树上某个节点的祖先就是灭绝以后会波及到这个节点的节点，那么我们就只需要在拓扑过程中同时在树上动态维护$LCA$（这里跳$LCA$只要暴力跳就行了），最后做树上前缀和求答案就行了。具体实现看代码。

　　Code：

 

//It is made by HolseLee on 13th Oct 2018
//Luogu.org P2012
#include<bits/stdc++.h>
using namespace std;

const int N=2e6+7;
int n,head[N],cnte,fa[N],lca[N],h[N],cnt,ans[N],dg[N],dep[N];
struct Edge {
    int to,nxt;
}e[N<<2],edge[N<<2];
queue<int>t;

inline int read()
{
    char ch=getchar(); int num=0; bool flag=false;
    while( ch<'0' || ch>'9' ) {
        if( ch=='-' ) flag=false; ch=getchar();
    }
    while( ch>='0' && ch<='9' ) {
        num=num*10+ch-'0'; ch=getchar();
    }
    return flag ? -num : num;
}

inline void add(int x,int y)
{
    e[++cnte].to=y;
    e[cnte].nxt=head[x];
    head[x]=cnte;
}

inline void add_edge(int x,int y)
{
    edge[++cnt].to=y;
    edge[cnt].nxt=h[x];
    h[x]=cnt;
}

inline int LCA(int x,int y)
{
    if( !x || !y ) return 0;
    if( dep[x]<dep[y] ) swap(x,y);
    while( dep[x]>dep[y] ) x=fa[x];
    while( x!=y ) x=fa[x], y=fa[y];
    return x;
}

void dfs(int x)
{
    for(int i=h[x],y; i; i=edge[i].nxt) {
        y=edge[i].to;
        dfs(y);
        ans[x]+=(ans[y]+1);
    }
}

int main()
{
    memset(lca,-1,sizeof(lca));
    n=read(); 
    int x,y;
    for(int i=1; i<=n; ++i) {
        while( 555 ) {
            x=read(); if( !x ) break;
            add(x,i); dg[i]++;
        }
    }
    for(int i=1; i<=n; ++i) 
        if( !dg[i] ) t.push(i),add_edge(0,i),fa[i]=0,dep[i]=0;
    while( !t.empty() ) {
        x=t.front(); t.pop();
        for(int i=head[x]; i; i=e[i].nxt) {
            y=e[i].to; dg[y]--;
            if( lca[y]==-1 ) lca[y]=x;
            else lca[y]=LCA(lca[y],x);
            if( !dg[y] ) t.push(y),dep[y]=dep[lca[y]]+1, add_edge(lca[y],y),fa[y]=lca[y];
        }
    }
    dfs(0);
    for(int i=1; i<=n; ++i) printf("%d\n",ans[i]);
    return 0;
}