洛谷P3391文艺平衡树（Splay）

　　题目传送门

　　转载自https://www.cnblogs.com/yousiki/p/6147455.html，转载请注明出处

　　

经典引文

空间效率：O(n)

时间效率：O(log n)插入、查找、删除

创造者：Daniel Sleator 和 Robert Tarjan

优点：每次查询会调整树的结构，使被查询频率高的条目更靠近树根。

Tree Rotation

 

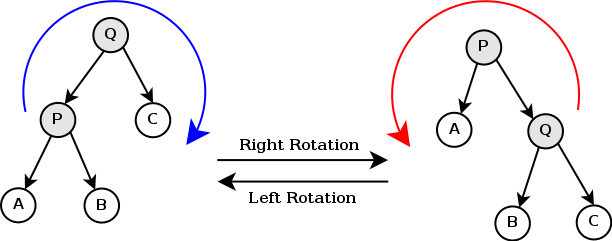
树的旋转是splay的基础，对于二叉查找树来说，树的旋转不破坏查找树的结构。

 

Splaying

 

Splaying是Splay Tree中的基本操作，为了让被查询的条目更接近树根，Splay Tree使用了树的旋转操作，同时保证二叉排序树的性质不变。

Splaying的操作受以下三种因素影响：

• 节点x是父节点p的左孩子还是右孩子
• 节点p是不是根节点，如果不是
• 节点p是父节点g的左孩子还是右孩子

同时有三种基本操作：

 

Zig Step

当p为根节点时，进行zip step操作。

当x是p的左孩子时，对x右旋；

当x是p的右孩子时，对x左旋。

 

Zig-Zig Step

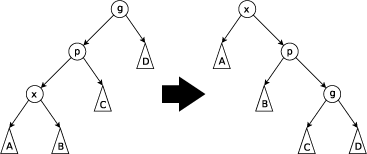
当p不是根节点，且x和p同为左孩子或右孩子时进行Zig-Zig操作。

当x和p同为左孩子时，依次将p和x右旋；

当x和p同为右孩子时，依次将p和x左旋。

 

 

Zig-Zag Step

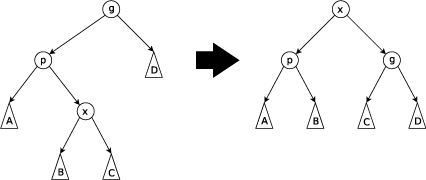
当p不是根节点，且x和p不同为左孩子或右孩子时，进行Zig-Zag操作。

当p为左孩子，x为右孩子时，将x左旋后再右旋。

当p为右孩子，x为左孩子时，将x右旋后再左旋。

 

 

应用

 

Splay Tree可以方便的解决一些区间问题，根据不同形状二叉树中序遍历结果不变的特性，可以将区间按顺序建二叉查找树。

每次自下而上的一套splay都可以将x移动到根节点的位置，利用这个特性，可以方便的利用Lazy的思想进行区间操作。

对于每个节点记录size，代表子树中节点的数目，这样就可以很方便地查找区间中的第k小或第k大元素。

对于一段要处理的区间[x, y]，首先splay x-1到root，再splay y+1到root的右孩子，这时root的右孩子的左孩子对应子树就是整个区间。

这样，大部分区间问题都可以很方便的解决，操作同样也适用于一个或多个条目的添加或删除，和区间的移动。

 

最后附上自己写的洛谷的模板题的代码：　

 

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+7;
int n,m,root,tot;
struct Node{
  int ch[2],size;
  int fa,mark,val;
  void add(int x,int y){
    ch[0]=ch[1]=mark=0;
    val=x;fa=y;size=1;}
}t[N];
inline int read()
{
  char ch=getchar();int num=0;bool flag=false;
  while(ch<'0'||ch>'9'){if(ch=='-')flag=true;ch=getchar();}
  while(ch>='0'&&ch<='9'){num=num*10+ch-'0';ch=getchar();}
  return flag?-num:num;
}
inline void pushup(int x)
{
  int l=t[x].ch[0],r=t[x].ch[1];
  t[x].size=t[l].size+t[r].size+1;
}
inline void pushdown(int x)
{
  if(t[x].mark){
    t[t[x].ch[0]].mark^=1;
    t[t[x].ch[1]].mark^=1;
    swap(t[x].ch[0],t[x].ch[1]);
    t[x].mark=0;}
}
inline void rotate(int x)
{
  int y=t[x].fa;
  int z=t[y].fa;
  int k=(t[y].ch[1]==x);
  t[z].ch[t[z].ch[1]==y]=x;
  t[x].fa=z;
  t[t[x].ch[k^1]].fa=y;
  t[y].ch[k]=t[x].ch[k^1];
  t[x].ch[k^1]=y;
  t[y].fa=x;
  pushup(y);pushup(x);
}
inline void splay(int x,int tag)
{
  while(t[x].fa!=tag){
    int y=t[x].fa;
    int z=t[y].fa;
    if(z!=tag)
      (t[y].ch[1]==x)^(t[z].ch[1]==y)?
    rotate(x):rotate(y);
    rotate(x);
  }
  if(tag==0)root=x;
}
inline void insert(int x)
{
  int now=root,fa=0;
  while(now)
    fa=now,now=t[now].ch[x>t[now].val];
  now=++tot;
  if(fa)t[fa].ch[x>t[fa].val]=now;
  t[now].add(x,fa);
  splay(now,0);
}
inline int find(int x)
{
  int now=root;
  while(555){
    pushdown(now);
    if(t[t[now].ch[0]].size>=x)now=t[now].ch[0];
    else if(t[t[now].ch[0]].size+1==x)return now;
    else x-=(t[t[now].ch[0]].size+1),now=t[now].ch[1];
  }
}
inline void work(int l,int r)
{
  l=find(l);r=find(r+2);
  splay(l,0);splay(r,l);
  t[t[t[root].ch[1]].ch[0]].mark^=1;
}
inline void print(int x)
{
  pushdown(x);
  if(t[x].ch[0])print(t[x].ch[0]);
  if(t[x].val>1&&t[x].val<n+2)
    printf("%d ",t[x].val-1);
  if(t[x].ch[1])print(t[x].ch[1]);
}
int main()
{
  n=read();m=read();
  for(int i=1;i<=n+2;i++)
    insert(i);
  for(int i=1;i<=m;i++){
    int l=read();int r=read();
    work(l,r);}
  print(root);
  return 0;
}