频域滤波
1、频域滤波的步骤小结
1、给定一副大小为M*N的输入图像 ,首先得到填充参数P和Q,通常填充
,首先得到填充参数P和Q,通常填充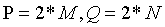 (满足
(满足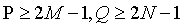 )。
)。
2、对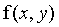 添加必要数量的0,形成大小P*Q的填充图像。
添加必要数量的0,形成大小P*Q的填充图像。
3、添加的虚部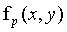 ,全部为0即可,合并成新的Mat对象
,全部为0即可,合并成新的Mat对象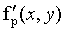 。
。
4、计算步骤3的图像的DFT,得到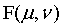 ,这里要将
,这里要将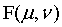 进行
进行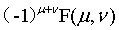 变换。
变换。
5、根据相应的算法生成P*Q大小的滤波函数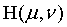 ,用阵列相乘
,用阵列相乘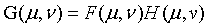 .
.
6、将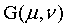 进行
进行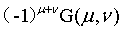 变换,然后对
变换,然后对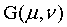 进行IDFT变换。
进行IDFT变换。
2、填充图像
填充图像主要是将图像由MN大小填充到PN大小,这里要满足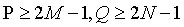 。
。
填充常数0。这样做的主要原因是避免循环卷积中的缠绕错误。常见的填充大小为P=2M,Q=2N。
2.1、填充代码
void paddingPQ(Mat& src, Mat& dst)
{
//要求输入一张单通道图片
//输入图像f(x,y) 通常P=2M Q=2N 这里填充为常量0
int M = src.rows;//高
int N = src.cols;//宽
cout << "M N" << M << " " << N << endl;
dst = Mat::zeros(Size(2 * N, 2 * M), CV_8UC1);
for (int i = 0; i < M; i++)
{
for (int j = 0; j < N; j++)
{
dst.at<uchar>(i, j) = src.at<uchar>(i, j);
}
}
}
2.2、填充结果
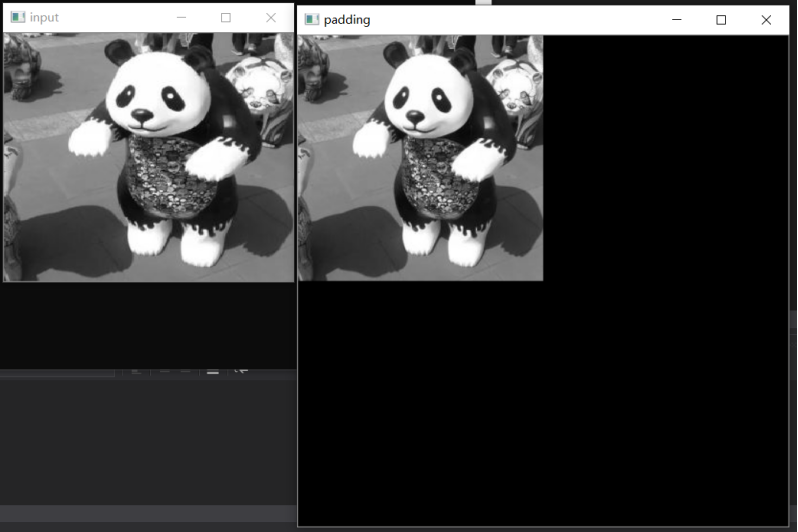
3 灰度图像的DFT和IDFT变换
3.1 DFT
1、对于输入一张灰度图片如果是CV_8UC1的,先转换成CV_32FC1。
2、构建输入图片的虚部,这也是一个CV_32F的Mat对象,数据全0就可以了。
3、将实部和虚部合并成一个Mat对象,调用dft()函数。
4、对步骤3得到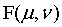 的乘以
的乘以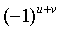 ,主要是将四个角的低频部分转换到中间。
,主要是将四个角的低频部分转换到中间。
5、计算实部和虚部的幅度值 ,并用
,并用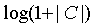 ,转换灰度值的范围(这步主要是为了方便观察)。
,转换灰度值的范围(这步主要是为了方便观察)。
6、展示处理结果。
3.2 DFT代码
void takeDFT(Mat& source, Mat& destination)
{
// CV_8UC1 to CV_32FC1
Mat originalFloat;
source.convertTo(originalFloat, CV_32FC1, 1.0 / 255.0);
// ready dft data complex;
Mat originalComplex[2] = { originalFloat,Mat::zeros(originalFloat.size(),CV_32F) };
Mat dftOriginal;
merge(originalComplex, 2, dftOriginal);
dft(dftOriginal, destination, DFT_COMPLEX_OUTPUT);
}
void showDFT(Mat& source)
{
Mat sourceComplex[2];
split(source, sourceComplex);
Mat logReady;
magnitude(sourceComplex[0], sourceComplex[1], logReady);
logReady += Scalar::all(1);
log(logReady, logReady);
changeQuadrant(logReady);
normalize(logReady, logReady, 0, 1, NORM_MINMAX);
namedWindow("spectrum", WINDOW_FREERATIO);
imshow("spectrum", logReady);
}
void changeQuadrant(Mat& source)
{
//draw spectrum
int cx = source.cols / 2;
int cy = source.rows / 2;
Mat q0(source, Rect(0, 0, cx, cy));
Mat q1(source, Rect(cx, 0, cx, cy));
Mat q2(source, Rect(0, cy, cx, cy));
Mat q3(source, Rect(cx, cy, cx, cy));
Mat tmp;
q0.copyTo(tmp);
q3.copyTo(q0);
tmp.copyTo(q3);
q1.copyTo(tmp);
q2.copyTo(q1);
tmp.copyTo(q2);
}
3.3、DFT效果
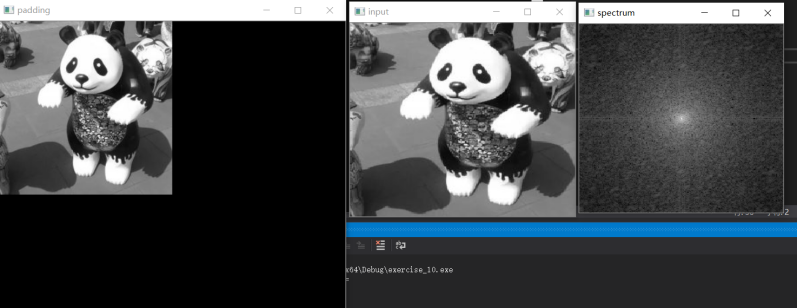
4 IDFT
IDFT基本步骤
1、将包含实部和虚部的数据信息的Mat对象,调用下idft()函数就可以,后面实验都有我就不做单独演示。
注意:如果前面做了象限的转换(将低频转到中间)这个步骤,现在做一下逆过程。
5 理想低通滤波器
对于做了DFT变换的图像,高频主要是图像中的细节信息,如果做低通滤波,保留的就是直流分量。大致的讲就是让图片变得模糊。其实这也告诉我们空域的卷积和频域的点乘可以达到同样的效果。
在原点为圆心,以为半径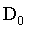 的圆内,无衰减的通过所有的频率,而圆外阻断所有的频率的低通滤波器称为理想低通滤波器(ILPF),它的的定义为
的圆内,无衰减的通过所有的频率,而圆外阻断所有的频率的低通滤波器称为理想低通滤波器(ILPF),它的的定义为
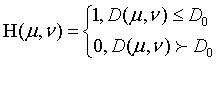
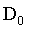 是一个正常值,
是一个正常值,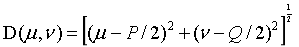 表示中心点到频域中心的距离。
表示中心点到频域中心的距离。
具体步骤:
1、创建P*Q的理想低通滤波过滤器
2、频域滤波,然后IDFT变换到空域。
5.1 理想低通滤波器实现代码
void make_ILPE_filter(int width, int height, double D0,Mat& dst)
{
dst = Mat::zeros(Size(width, height), CV_32F);
double D0_2 = pow(D0, 2);
double half_h = height * (1.0) / 2;
double half_w = width * (1.0) / 2;
//创建理想低通滤波器
for (int i = 0; i < height; i++)
{
for (int j = 0; j < width; j++)
{
double distance = pow((half_h - (double)i), 2) + pow((half_w - (double)j), 2);
if (less<double>()(distance,D0_2)) {
dst.at<float>(i, j) = 1;
}
}
}
}
void iILPF(Mat& src, Mat& dst, double D0)
{
//这里输入的src是刚通过DFT处理后的Mat 并没有进行其他的处理
//先将低频高亮部分移到中间
changeQuadrant(src);
//Mat sourceComplex[2];
//split(src, sourceComplex);
//创建低通滤波器
Mat ifilter;
make_ILPE_filter(src.cols, src.rows, D0, ifilter);
Mat sourceComplex[2];
split(src, sourceComplex);
Mat temp[2];
multiply(sourceComplex[0], ifilter, temp[0]);
multiply(sourceComplex[1], ifilter, temp[1]);
Mat idft;
merge(temp, 2, idft);
//转换回相应的象限
changeQuadrant(idft);
dft(idft, dst, DFT_INVERSE | DFT_REAL_OUTPUT | DFT_SCALE);
imshow("理想低通滤波", dst);
}
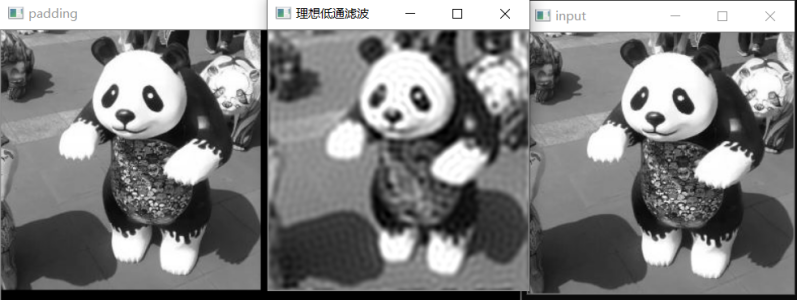
5.3理想低通滤波器实验效果
ILPE 并不实用,ILPE在空间域的振铃现象是特别的明显。
这里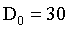 ,很明显过滤掉了很多细节。
,很明显过滤掉了很多细节。
6 理想高通滤波器
理想高通滤波器和理想低通滤波器功能相反,主要是保留图片的细节。
在原点为圆心,以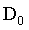 为半径的圆内,阻断通过所有的频率,而圆外通过所有的频率的高通通滤波器称为理想高通滤波器(IHPF),它的的定义为
为半径的圆内,阻断通过所有的频率,而圆外通过所有的频率的高通通滤波器称为理想高通滤波器(IHPF),它的的定义为
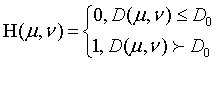
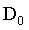 是一个正常值,截止频率,
是一个正常值,截止频率,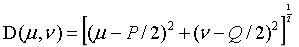 表示中心点到频域中心的距离
表示中心点到频域中心的距离
6.1、理想高通滤波器实现代码
void make_IHPE_filter(int width, int height, double D0, Mat& dst)
{
dst = Mat::ones(Size(width, height), CV_32F);
double D0_2 = pow(D0, 2);
double half_h = height * (1.0) / 2;
double half_w = width * (1.0) / 2;
//创建理想高通滤波器
for (int i = 0; i < height; i++)
{
for (int j = 0; j < width; j++)
{
double distance = pow((half_h - (double)i), 2) + pow((half_w - (double)j), 2);
if (less<double>()(distance, D0_2)) {
dst.at<float>(i, j) = 0;
}
}
}
}
void iHLPF(Mat& src, Mat& dst, double D1)
{
//这里输入的src是刚通过DFT处理后的Mat 并没有进行其他的处理
//先将低频高亮部分移到中间
changeQuadrant(src);
Mat ifilter;
make_IHPE_filter(src.cols, src.rows, D1, ifilter);
Mat sourceComplex[2];
split(src, sourceComplex);
Mat temp[2];
multiply(sourceComplex[0], ifilter, temp[0]);
multiply(sourceComplex[1], ifilter, temp[1]);
Mat idft;
merge(temp, 2, idft);
//转换回相应的象限
changeQuadrant(idft);
dft(idft, dst, DFT_INVERSE | DFT_REAL_OUTPUT | DFT_SCALE);
imshow("理想高通滤波", dst);
}
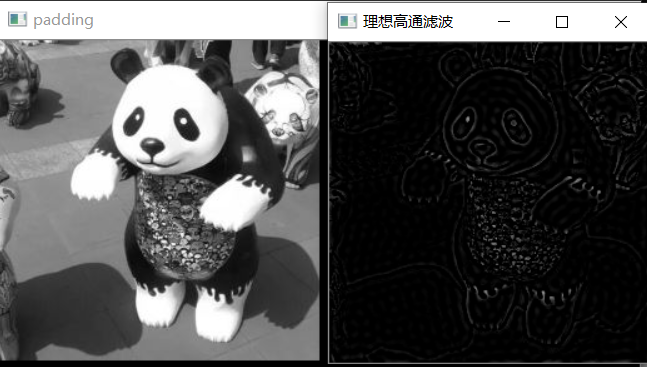
6.2、理想高通滤波器效果
IHPF和ILPF一样具有相同的振铃性质。
这里截止频率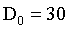
7 布特沃斯高通滤波器
布特沃斯高通滤波器的定义:
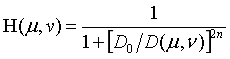
布特沃斯高通滤波器比理想高通滤波器更平滑,这里的n是阶数,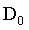 是截止频率。
是截止频率。
7.1布特沃斯高通滤波器实现
void make_BHPF_filter(int width, int height, double D0,double n, Mat& dst)
{
dst = Mat::ones(Size(width, height), CV_32F);
double D0_2 = pow(D0, 2);
double half_h = height * (1.0) / 2;
double half_w = width * (1.0) / 2;
//创建理想高通滤波器
for (int i = 0; i < height; i++)
{
for (int j = 0; j < width; j++)
{
double distance = pow((half_h - (double)i), 2) + pow((half_w - (double)j), 2);
double temp = pow(D0 / sqrt(distance), 2 * n);
dst.at<float>(i, j) = 1.0 / (1.0 + temp);
}
}
}
void iBHPF(Mat& src, Mat& dst, double D1,double n)
{
//这里输入的src是刚通过DFT处理后的Mat 并没有进行其他的处理
//先将低频高亮部分移到中间
changeQuadrant(src);
Mat ifilter;
make_BHPF_filter(src.cols, src.rows, D1,n, ifilter);
Mat sourceComplex[2];
split(src, sourceComplex);
Mat temp[2];
multiply(sourceComplex[0], ifilter, temp[0]);
multiply(sourceComplex[1], ifilter, temp[1]);
Mat idft;
merge(temp, 2, idft);
//转换回相应的象限
changeQuadrant(idft);
dft(idft, dst, DFT_INVERSE | DFT_REAL_OUTPUT | DFT_SCALE);
imshow("布特沃斯高通滤波", dst);
}
7.2 布特沃斯高通滤波器实验效果
n=2 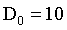

n=2 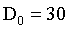

n=2 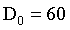

8 布特沃斯低通滤波器
布特沃斯低通滤波器的定义:
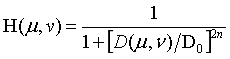
这里的n是阶数,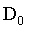 是截止频率。BLPF传递函数并没有通过频率和滤除频率之间给出明显截止的急剧不连续性,基本上没有振铃现象。
是截止频率。BLPF传递函数并没有通过频率和滤除频率之间给出明显截止的急剧不连续性,基本上没有振铃现象。
8.1布特沃斯低通滤波器代码实现
void make_BIPF_filter(int width, int height, double D0, double n, Mat& dst)
{
dst = Mat::ones(Size(width, height), CV_32F);
double D0_2 = pow(D0, 2);
double half_h = height * (1.0) / 2;
double half_w = width * (1.0) / 2;
//布特沃斯低通滤波器
for (int i = 0; i < height; i++)
{
for (int j = 0; j < width; j++)
{
double distance = pow((half_h - (double)i), 2) + pow((half_w - (double)j), 2);
double temp = pow(sqrt(distance)/D0, 2 * n);
dst.at<float>(i, j) = 1.0 / (1.0 + temp);
}
}
}
void iBIPF(Mat& src, Mat& dst, double D1, double n)
{
//这里输入的src是刚通过DFT处理后的Mat 并没有进行其他的处理
//先将低频高亮部分移到中间
changeQuadrant(src);
Mat ifilter;
make_BIPF_filter(src.cols, src.rows, D1, n, ifilter);
Mat sourceComplex[2];
split(src, sourceComplex);
Mat temp[2];
multiply(sourceComplex[0], ifilter, temp[0]);
multiply(sourceComplex[1], ifilter, temp[1]);
Mat idft;
merge(temp, 2, idft);
//转换回相应的象限
changeQuadrant(idft);
dft(idft, dst, DFT_INVERSE | DFT_REAL_OUTPUT | DFT_SCALE);
imshow("布特沃斯低通滤波", dst);
}
8.2布特沃斯低通滤波器实验效果
BLPF传递函数并没有通过频率和滤除频率之间给出明显的截止的急剧不连续。使用BLPF处理过的图像基本没有振铃现象。
空间域的一阶布特沃斯滤波器没有振铃现象,二阶中,振铃现象通常很难察觉,但是更高阶数的滤波器中振铃现象会很明显。
阶数越大,越接近理想滤波器。
n=2 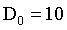

n=2 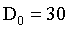

n=2 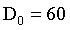

9、实验过程遇到的问题
1、虽然实验是自己做的也完成了,但是傅里叶变换的推导公式哪里还是有些懵懵的,之前学的时候搞懂了,现在又忘了。
2、实验中观察振铃现象,具体的频谱图我没记录下来,后面改进的时候将这部分代码单独拎出来。
后记
1、幅度谱决定了一副图像含有的各种频率分量的多少,相位谱决定每种频率分量的位置,通常在图像处理中是不用处理相位谱的。
2、先对图像做0填充,然后创建尺寸与填充图像一样大的滤波器,这会导致缠绕错误,因为没有对该滤波器进行填充。但是这种方式的错误可以通过
图像填充提供间隔有效地减轻,并且尽力消除振铃现象(本次实验中采用的方法是填充为P*Q大小)。
3、另外一种思路构建一个与图像尺寸大小相同的滤波器,然后计算它的空域滤波器,然后在空域进行填充,然后再计算IDF返回频域。这种方式会由于
频域滤波器的空间上具有无限扩展的成分,任何0填充的空间截断将引入不连续,通常会在频率域导致振铃现象(一般情况)。
4、以上的方法由于相位角与实部和虚部之比有关,改变实部和虚部并没有改变相位,我们称这样的滤波器为“零相移滤波器”。
5、 高斯滤波器没有振铃现象。




