图片直方图均衡化
对于输入像素点r和输出像素点s都在灰度级 [0,L-1]之间,r = 0 代表黑色, r = L - 1代表白色。对于r和s的变换形式为:

r和s满足一下条件:
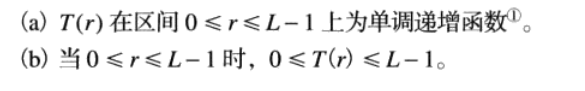
利用反函数来从s推r时,有以下定义:
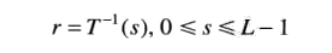
r和s满足条件:
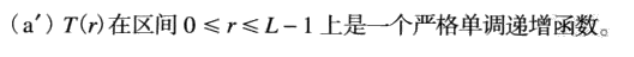
条件a是为了保证输出的灰度级不少于输入,这是为了防止二义性。条件b是为了保证输出的灰度范围和输入的灰度范围相同。条件a`也是为了保证s到r 也是一一对应的,防止二义性。实验中采用8bit整性的像素分布,不一定满足这个情况。
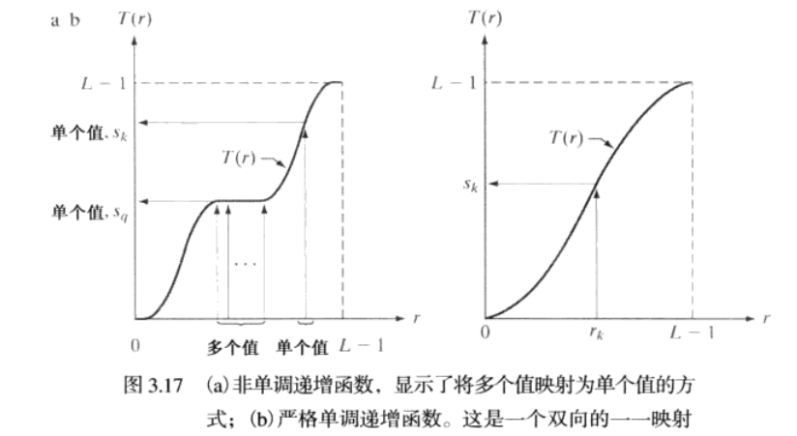
在实验中会类似左边的图像,出现多个输入的r,输出同一个s值。而在理论的约束上应该和右图相似,r与s一一对应。
对于一副灰度图像,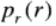
和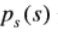
分别代表输入图像和输出图像的像素点的概率分布,我们简称为PDF。对于已知的和满足公式:
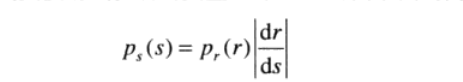
(1)
直方图均衡化的采用的公式如下:
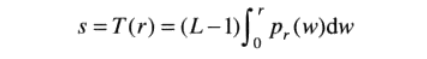
(2)
其中w是积分假变量,L-1是最大的灰度级。
为什么要这么做呢。由莱布尼兹准则,我们知道上限的定积分的导数是被积函数在该上限的值。
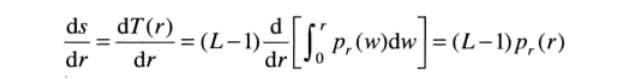
(3)
我们将的结果带入(1)中,
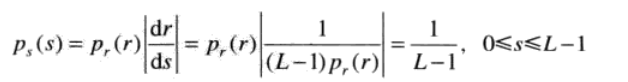
(4)
2 结论
使用(2)公式后,输出图像的像素点s分布是均匀的,PDF为1/(L-1)。

3 离散直方图均衡化采用公式
对于离散的直方图均衡化采用的公式为:
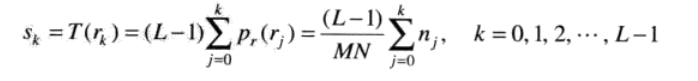
(5)
其中MN是总的像素点个数
编码实现
1 统计输入的灰度图像的像素信息
void calHistInfo(const Mat& src, vector<unsigned int>& calVec, vector<unsigned int >& calVecBefor,unsigned int LMax){
int width = src.cols;
int height = src.rows;
int piexl = 0;
for (int h = 0; h < height; h++)
{
for (int w = 0; w < width; w++) {
piexl = (int)src.at<uchar>(h, w);
calVec[round(piexl)] += 1;
}
}
calVecBefor[0] = calVec[0];
for (int i = 1; i < calVec.size(); i++)
{
calVecBefor[i] = calVecBefor[i - 1] + calVec[i];
}
cout << "统计完毕" << endl;
}
这里我用了两个vector数组calVec 和calVecBefor ,calVec是用于记录每个灰度级别的像素个数,
calVecBefor是记录在当前像素r个数和r之前的像素之和。LMax是用于记录有多少个灰度级别,这里LMax =256。
2 根据直方图统计信息绘制折线图
void showHistChart(Mat& canvas,unsigned int LMax,vector<unsigned int> calVec,Scalar sca, int thikness)
{
//横轴是灰度级
//纵轴是像素的分布情况,我采取的方法是像素数目最多的为单位1
int canvas_height = canvas.rows;
int canvas_step = canvas.cols / LMax;
auto it = max_element(calVec.begin(), calVec.end());
unsigned int calMax = *it;
//开始画折线图
for (int i = 0; i < LMax-1; i++)
{
line(canvas, Point(i * canvas_step, canvas_height - (canvas_height*(1.0)*calVec[i]/calMax)),
Point((i + 1) * canvas_step, canvas_height - (canvas_height * (1.0) * calVec[i+1] / calMax)),
sca, thikness, 8);
}
}
其中canvas是画布,首先要找到像素点最多的灰度级别和该级别像素的个数calMax,以及根据画布大小和灰度级个数确定步长canvas_step,sca是画折线使用的颜色, thikness是折线的粗细,参数8是渲染方式。
3 确定像素点r与s之间的映射
void createRSTable(const vector<unsigned int>& calVecBefor,
unordered_map<unsigned int,unsigned int>& table_rs,unsigned int LMax)
{
double total = (double)calVecBefor[LMax - 1];
for (int i =0;i<LMax;i++)
{
double s = LMax*(double)calVecBefor[i] * (1.0) / total;
if (round(s) <= 255) {
table_rs.insert(make_pair(i, round(s)));
}
else
{
table_rs.insert(make_pair(i, 255));
}
}
}
这里我采用的unordered_map用于记录输入的r与输出的s之间的映射关系。当然这里也可以用数组之类的记录,记录方法就是公式(5)。
4 灰度图像的直方图均衡化
void iHistImp(Mat& src, Mat&dst, unordered_map<unsigned int,unsigned int>& table_rs) {
dst = Mat::zeros(src.size(), src.type());
int width = src.cols;
int height = src.rows;
int piexl = 0;
for (int h = 0; h < height; h++)
{
for (int w = 0; w < width; w++) {
piexl = (int)src.at<uchar>(h, w);
auto it = table_rs.find(piexl);
if (it != table_rs.end())
{
dst.at<uchar>(h, w) = it->second;
}
}
}
}
这里通过遍历灰度输入的输入像素点r,来找到相应的输出s。
5 灰度图像直方图均衡化的结果

这里我除了使用自己实现的直方图均衡化,还调用opencv中直方图均衡化的api,来对比实验效果。
实验前后的折线图:
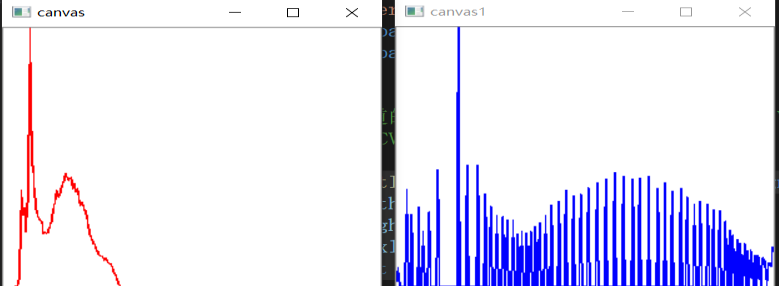
红色是直方图均衡化前的像素统计,蓝色是均衡化后的像素统计。
6 彩色图像的直方图均衡化
彩色图像的直方图均衡化,我是将输入的彩色图像分成bgr三个通道,分别进行直方图均衡化,然后再将结果合并再一起。
/*
* 彩色图像的直方图均衡化
*/
void BGRHist(Mat& src, Mat& dst)
{
//将彩色图像的按照BGR三个通道切分
vector<Mat> splitMat;
split(src,splitMat);
//分别对bgr 三个通道进行直方图均衡化
vector<Mat> mergeMat;
split(src, mergeMat);
for (int i = 0; i < 3; i++)
{
unsigned int LMax = 256;
vector<unsigned int> calVec(LMax, 0);
vector<unsigned int > calVecBefor(LMax, 0);//用于记录灰度级l之前的所以的像素点个数
calHistInfo(splitMat[i], calVec, calVecBefor, LMax);
//构建输入像素r 与输出像素s 之间的 一一映射表
unordered_map<unsigned int, unsigned int > table_rs;
createRSTable(calVecBefor, table_rs, LMax);
iHistImp(splitMat[i],mergeMat[i], table_rs);
}
merge(mergeMat,dst);
}
彩色图像直方图均衡化的结果:
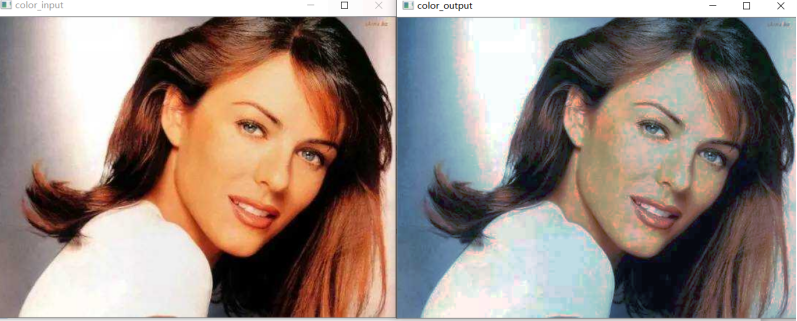
实验中的问题以及需要改进的地方
1、在实验的像素的统计过程和r与s转换的过程,可以采用基于指针的方式遍历。
2、彩色图像的直方图均衡化效果不是很好,可以尝试新的算法。
3、r与s的映射表可以转成用数组存放,可能要快点。
4、可以将r->s的值存为一个灰度级的映射表
5、可以对直方图均衡化的结果再进行直方图均衡化,可以设置迭代次数
直方图匹配(直方图规定化)
后面有空再实现
局部直方图处理
后面再实现
后记
1、使用高频强调滤波,然后再使用直方图均衡,可以更好的处理图片。《数字图像处理·第三版》P181 有介绍类似的方法。




