透视矫正插值公式的几何证明

透视矫正插值公式(Perspective-Correct Interpolation)在计算机图形学书一般很少给出证明，我见到过《3D游戏与计算机图形学中的数学方法》的证明，是用解析几何硬算，过程只是验证结论而已。这里给出两个几何证明。

问题重新描述为：如上图，在三角形ADC中，E在AD上，G在CD上，F为EG中点，DF交AC于B，过D点的虚线//EG；A、B、C到虚线的距离分别为h1、h2、h3, 则 1/h2 是 1/h1+1/h3 的1/2.

一般地，若 EF = kFG，则 (1/h1 - 1/h2) = k(1/h2 - 1/h3).

 

下面来自叶中豪先生简洁明快的证明。叶中豪，国内首屈一指的近代欧氏几何大师，上海十大藏书家。

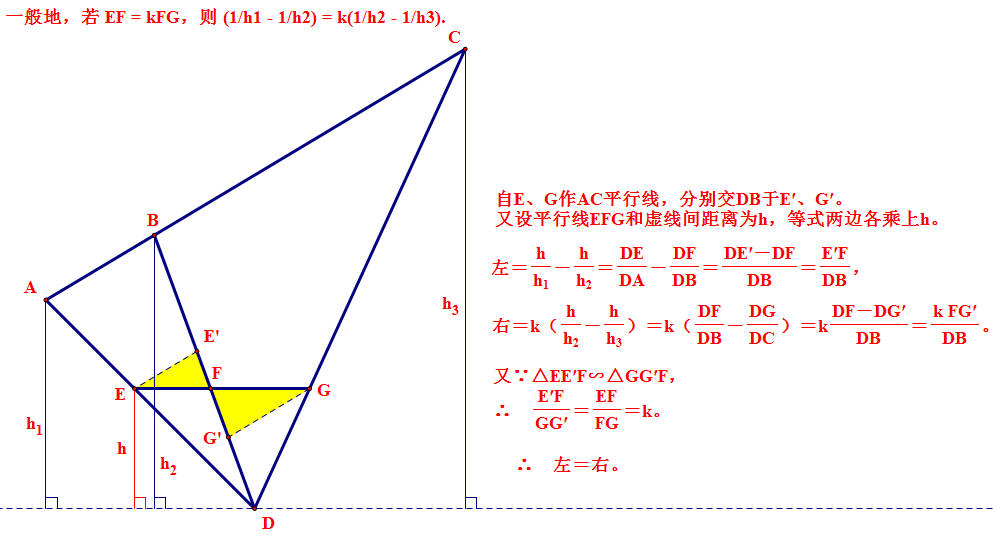
不怕在叶老师面前班门弄斧，下面也给出我的一个思路：

之所以要给出几何的证明，是因为解析的证明大都只是在验证结论，容易淹没在冗长的代数运算中。而几何的证明更直观，更能使你看到结论的本质所在。透视矫正插值公式很神奇，在3D图形学基础中几乎是个谜，大部分的3D技术书籍都是直接使用结论，很少有人追究它为什么成立，是怎么发现的。期待有人给出更简短更本质的证明。

参考：《来自显卡的几何题》http://forum.cnool.net/topic_show.jsp?id=6285906&oldpage=1&thesisid=494&flag=topic1