奇环,二分图相关 785, 2493

使用着色法来判定一个图是否为二分图，或者是否包含奇环（包含奇环的话就不是二分图）

 

785. Is Graph Bipartite?

There is an undirected graph with n nodes, where each node is numbered between 0 and n - 1. You are given a 2D array graph, where graph[u] is an array of nodes that node u is adjacent to. More formally, for each v in graph[u], there is an undirected edge between node u and node v. The graph has the following properties:

• There are no self-edges (graph[u] does not contain u).
• There are no parallel edges (graph[u] does not contain duplicate values).
• If v is in graph[u], then u is in graph[v] (the graph is undirected).
• The graph may not be connected, meaning there may be two nodes u and v such that there is no path between them.

A graph is bipartite if the nodes can be partitioned into two independent sets A and B such that every edge in the graph connects a node in set A and a node in set B.

Return true if and only if it is bipartite.

 

Example 1:

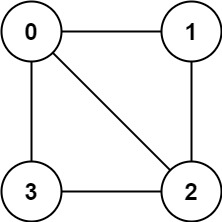
Input: graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
Output: false
Explanation: There is no way to partition the nodes into two independent sets such that every edge connects a node in one and a node in the other.

Example 2:

Input: graph = [[1,3],[0,2],[1,3],[0,2]]
Output: true
Explanation: We can partition the nodes into two sets: {0, 2} and {1, 3}.

Constraints:

• graph.length == n
• 1 <= n <= 100
• 0 <= graph[u].length < n
• 0 <= graph[u][i] <= n - 1
• graph[u] does not contain u.
• All the values of graph[u] are unique.
• If graph[u] contains v, then graph[v] contains u.

class Solution {
    public boolean isBipartite(int[][] graph) {
        // 定义color用于存储各节点颜色
        int[] color = new int[graph.length];
        // 遍历所有节点
        for(int i = 0; i < graph.length; i++) {
            // 如果不为0说明已经遍历过
            if(color[i] == 0) {
                // 如果不满足直接返回false
                if(!helper(graph, i, color, 1)) return false;
            }
        }
        return true;
    }
    private boolean helper(int[][] graph, int curr, int[] color, int last) {
        if(color[curr] != 0) {
            // 如果已经标记过颜色， 检查是否与前一个元素颜色相反，直接返回
            return color[curr] * last < 0;
        }
        // 标记当前点为上个点的相反颜色
        color[curr] = -last;
        // 遍历邻居节点
        for(int other : graph[curr]) {
            if(!helper(graph, other, color, color[curr])) return false;
        }
        return true;
    }
}

2493. Divide Nodes Into the Maximum Number of Groups

You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.

You are also given a 2D integer array edges, where edges[i] = [ai, bi] indicates that there is a bidirectional edge between nodes ai and bi. Notice that the given graph may be disconnected.

Divide the nodes of the graph into m groups (1-indexed) such that:

• Each node in the graph belongs to exactly one group.
• For every pair of nodes in the graph that are connected by an edge [ai, bi], if ai belongs to the group with index x, and bi belongs to the group with index y, then |y - x| = 1.

Return the maximum number of groups (i.e., maximum m) into which you can divide the nodes. Return -1 if it is impossible to group the nodes with the given conditions.

 

Example 1:

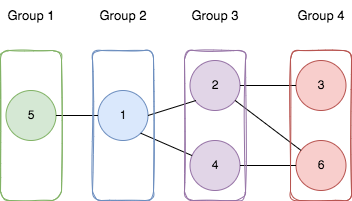
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
Output: 4
Explanation: As shown in the image we:
- Add node 5 to the first group.
- Add node 1 to the second group.
- Add nodes 2 and 4 to the third group.
- Add nodes 3 and 6 to the fourth group.
We can see that every edge is satisfied.
It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.

Example 2:

Input: n = 3, edges = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied.
It can be shown that no grouping is possible.

 Constraints:

• 1 <= n <= 500
• 1 <= edges.length <= 104
• edges[i].length == 2
• 1 <= ai, bi <= n
• ai != bi
• There is at most one edge between any pair of vertices.

class Solution {
    /*
    题目关键点：
    1. 是否为合法graph，如果存在奇环的话，无法对node进行切分
    2. 如果是合法graph，那么将连通图中各点作为定点进行bfs层级遍历，求出最大层级即为最大可切分group
     */
    private List<Integer> list = new ArrayList<>();
    int[] color;
    public int magnificentSets(int n, int[][] edges) {
        color = new int[n];
        // 建图
        List<Integer>[] graph = new List[n];
        for(int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        for(int[] edge : edges) {
            int s = edge[0] - 1, e = edge[1] - 1;
            graph[s].add(e);
            graph[e].add(s);
        }
        // check if valid
        int result = 0;
        for(int i = 0; i < n; i++) {
            // 已经遍历过了
            if(color[i] != 0) continue;

            // 检查当前点连接的graph
            list.clear();
            // 如果是奇环，直接返回-1
            if(!isValid(graph, i, 1)) return -1;
            // 从各个点尝试bfs，找到最大分层
            int max = 0;
            for(int node : list) {
                max = Math.max(max, bfs(graph, node));
            }
            result += max;
        }
        return result;
    }

    private int bfs(List<Integer>[] graph, int start) {
        Queue<Integer> queue = new LinkedList<>();
        boolean[] visited = new boolean[graph.length];
        queue.offer(start);
        visited[start] = true;
        int step = 0;
        while(!queue.isEmpty()) {
            int size = queue.size();
            for(int i = 0; i < size; i++) {
                int curr = queue.poll();
                for(int other : graph[curr]) {
                    if(visited[other]) continue;
                    visited[other] = true;
                    queue.offer(other);
                }
            }
            step++;
        }
        return step;
    }

    // 检查是否为奇环 
    private boolean isValid(List<Integer>[] graph, int curr, int lastColor) {
        if(color[curr] * lastColor > 0) return false;
        if(color[curr] * lastColor < 0) return true;
        list.add(curr);
        color[curr] = lastColor * -1;
        for(int other : graph[curr]) {
            if(!isValid(graph, other, color[curr])) return false;
        }
        return true;
    }
}