sorted matrix 系列 378, 240, 3027

 

378. Kth Smallest Element in a Sorted Matrix

 

Solved

Medium

 

Topics

 

Companies

Given an n x n matrix where each of the rows and columns is sorted in ascending order, return the kth smallest element in the matrix.

Note that it is the kth smallest element in the sorted order, not the kth distinct element.

You must find a solution with a memory complexity better than O(n2).

Example 1:

Input: matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
Output: 13
Explanation: The elements in the matrix are [1,5,9,10,11,12,13,13,15], and the 8th smallest number is 13

Example 2:

Input: matrix = [[-5]], k = 1
Output: -5

Constraints:

• n == matrix.length == matrix[i].length
• 1 <= n <= 300
• -109 <= matrix[i][j] <= 109
• All the rows and columns of matrix are guaranteed to be sorted in non-decreasing order.
• 1 <= k <= n2

Follow up:

• Could you solve the problem with a constant memory (i.e., O(1) memory complexity)?
• Could you solve the problem in O(n) time complexity? The solution may be too advanced for an interview but you may find reading this paper fun.

解法一：

使用min heap存储每行的头元素，逐个遍历取出k个元素，

将该元素的右侧下一个元素压入heap，最终得到第k个元素

时间复杂度：O(Klog(N))

class Solution { 
    public int kthSmallest(int[][] matrix, int k) {
        int m = matrix.length, n = matrix[0].length, ans = -1; // For general, the matrix need not be a square
        PriorityQueue<int[]> minHeap = new PriorityQueue<>(Comparator.comparingInt(o -> o[0]));
        // 每行第一个元素放入heap
        for (int r = 0; r < Math.min(m, k); ++r)
            minHeap.offer(new int[]{matrix[r][0], r, 0});
        // 开始从heap中取出元素，数k个
        for (int i = 1; i <= k; ++i) {
            int[] top = minHeap.poll();
            // 当前元素的位置
            int x = top[1], y = top[2];
            ans = top[0];
            if (y + 1 < n) minHeap.offer(new int[]{matrix[x][y + 1], x, y + 1});
        }
        return ans;
    }
}

解法二：二分猜答案

时间复杂度：O(N) 

class Solution {
    public int kthSmallest(int[][] matrix, int k) {
        // 给定最大/最小值，二分猜答案
        long left = Integer.MIN_VALUE, right = Integer.MAX_VALUE;
        int result = 0;
        while(left <= right) {
            long mid = left + (right - left) / 2;
            // 如果比mid的元素小的个数少于k，那么需要往大了猜
            if(countSmallerOrEqual(matrix, mid) < k) {
                left = mid + 1;
            }
            // 如果比mid元素小的个数多于或者等于k，那么记录下来result，继续往小了猜
            else{
                result = (int)mid;
                right = mid - 1;
            }
        }
        return result;
    }
    private int countSmallerOrEqual(int[][] matrix, long mid) {
        int m = matrix.length, n = matrix[0].length;
        int result = 0;
        // 从右上角开始数
        int x = 0, y = n - 1;
        while(x < m && y >= 0) {
            // 如果比mid大，向左移动
            if(matrix[x][y] > mid) y--;
            // 如果比mid小，向下移动，并且记录当前行小于mid的元素
            else {
                result += y + 1;
                x++;
            }
        }
        return result;
    }
}

 

3027. Find the Number of Ways to Place People II

You are given a 2D array points of size n x 2 representing integer coordinates of some points on a 2D-plane, where points[i] = [xi, yi].

We define the right direction as positive x-axis (increasing x-coordinate) and the left direction as negative x-axis (decreasing x-coordinate). Similarly, we define the up direction as positive y-axis (increasing y-coordinate) and the down direction as negative y-axis (decreasing y-coordinate)

You have to place n people, including Alice and Bob, at these points such that there is exactly one person at every point. Alice wants to be alone with Bob, so Alice will build a rectangular fence with Alice's position as the upper left corner and Bob's position as the lower right corner of the fence (Note that the fence might not enclose any area, i.e. it can be a line). If any person other than Alice and Bob is either inside the fence or on the fence, Alice will be sad.

Return the number of pairs of points where you can place Alice and Bob, such that Alice does not become sad on building the fence.

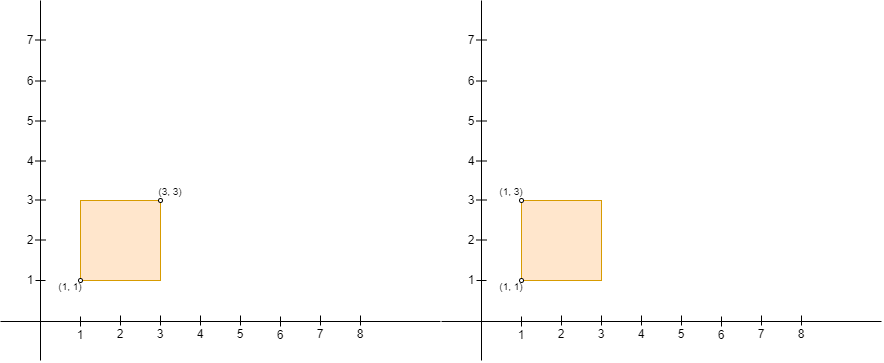
Note that Alice can only build a fence with Alice's position as the upper left corner, and Bob's position as the lower right corner. For example, Alice cannot build either of the fences in the picture below with four corners (1, 1), (1, 3), (3, 1), and (3, 3), because:

• With Alice at (3, 3) and Bob at (1, 1), Alice's position is not the upper left corner and Bob's position is not the lower right corner of the fence.
• With Alice at (1, 3) and Bob at (1, 1), Bob's position is not the lower right corner of the fence.

 

Example 1:

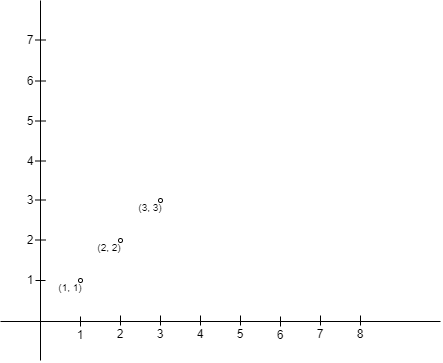
Input: points = [[1,1],[2,2],[3,3]]
Output: 0
Explanation: There is no way to place Alice and Bob such that Alice can build a fence with Alice's position as the upper left corner and Bob's position as the lower right corner. Hence we return 0. 

Example 2:

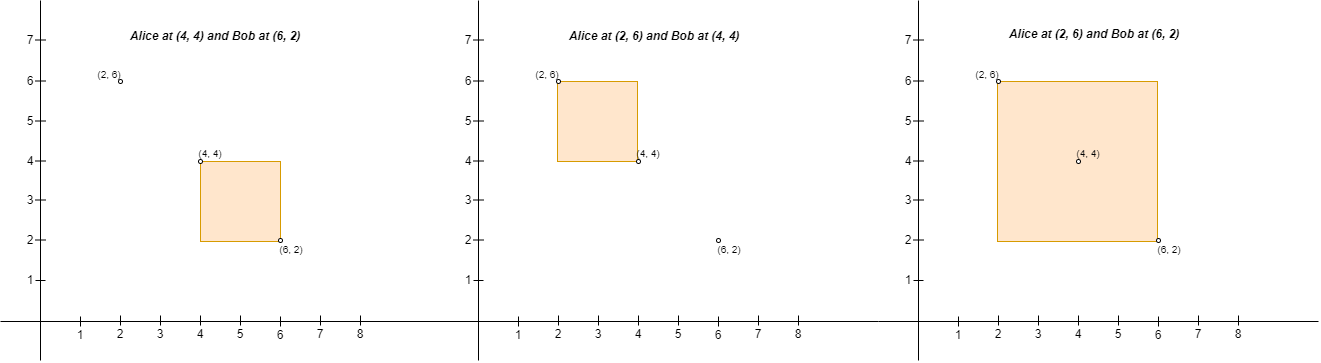
Input: points = [[6,2],[4,4],[2,6]]
Output: 2
Explanation: There are two ways to place Alice and Bob such that Alice will not be sad:
- Place Alice at (4, 4) and Bob at (6, 2).
- Place Alice at (2, 6) and Bob at (4, 4).
You cannot place Alice at (2, 6) and Bob at (6, 2) because the person at (4, 4) will be inside the fence.

Example 3:

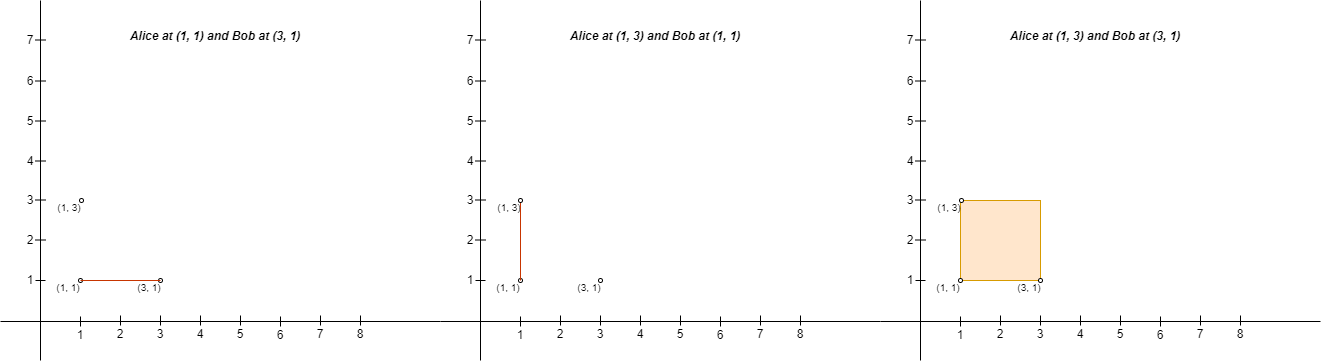
Input: points = [[3,1],[1,3],[1,1]]
Output: 2
Explanation: There are two ways to place Alice and Bob such that Alice will not be sad:
- Place Alice at (1, 1) and Bob at (3, 1).
- Place Alice at (1, 3) and Bob at (1, 1).
You cannot place Alice at (1, 3) and Bob at (3, 1) because the person at (1, 1) will be on the fence.
Note that it does not matter if the fence encloses any area, the first and second fences in the image are valid.

Constraints:

• 2 <= n <= 1000
• points[i].length == 2
• -109 <= points[i][0], points[i][1] <= 109
• All points[i] are distinct.

时间复杂度：O(N³)

class Solution {
    public int numberOfPairs(int[][] points) {
        // 对节点进行排序，x轴正向排，y轴倒序排，这样符合左上/右下的顺序
        Arrays.sort(points, (a, b) -> {
            if(a[0] == b[0]) return b[1] - a[1];
            return a[0] - b[0];
        });
        // 对节点开始两两匹配
        int result = 0;
        for(int i = 0; i < points.length; i++) {
            int[] alice = points[i];
            for(int j = i + 1; j < points.length; j++) {
                int[] bob = points[j];
                // x轴无需担心，因为我们是优先按照x轴排的，因此bob肯定在alice右侧
                // y轴需要考虑，如果bob跑到了alice的上面，那么不符合条件
                if(alice[1] < bob[1]) continue;
                // 接下来还得判断i和j中间的点有没有落到alice和bob范围的点
                boolean flag = false;
                for(int k = i + 1; k < j; k++) {
                    int[] mid = points[k];
                    // 依旧是只需要考虑y轴，因为x轴必然在两者之间
                    if(alice[1] >= mid[1] && mid[1] >= bob[1]) {
                        flag = true;
                    }
                }
                if(!flag) result++;
            }
        }
        return result;

    }
}

下面进行优化：时间复杂度 O(N²)

class Solution {
    public int numberOfPairs(int[][] points) {
        // 对节点进行排序，x轴正向排，y轴倒序排，这样符合左上/右下的顺序
        Arrays.sort(points, (a, b) -> {
            if(a[0] == b[0]) return b[1] - a[1];
            return a[0] - b[0];
        });
        // 对节点开始两两匹配
        int result = 0;
        for(int i = 0; i < points.length; i++) {
            int[] alice = points[i];
            int max = Integer.MIN_VALUE;//初始化i和j之间的点的y最高值
            for(int j = i + 1; j < points.length; j++) {
                int[] bob = points[j];
                if(alice[1] < bob[1]) continue;
                // 如果bob超过了中间点的最大值，那么满足，并且更新bob的y值为max
                if(bob[1] > max) {
                    max = bob[1];
                    result++;
                }
            }
        }
        return result;

    }
}