正规方程 Normal Equation

正规方程 Normal Equation

前几篇博客介绍了一些梯度下降的有用技巧，特征缩放（详见http://blog.csdn.net/u012328159/article/details/51030366）和学习率（详见http://blog.csdn.net/u012328159/article/details/51030961）。在线性回归中。为了求得參数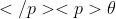的最优值，一般採用梯度下降和本文将要介绍的正规方程（normal equation）。

相比較梯度下降採用多次迭代逼近的方式。normal equation採用矩阵运算能够直接求解出參数。先介绍下什么是normal equation，如果一个数据集X有m个样本，n个特征。则如果函数为： 。数据集X的特征向量表示为：

表示第i个训练样本，表示第i个训练样本的第j个特征。之所以在X中加了第一列全为1，是为了让

若希望如果函数可以拟合Y，则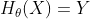。又由于 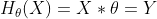 ，所以可以通过矩阵运算求出參数。

熟悉线性代数的同学应该知道怎么求出參数。可是前提是矩阵X存在逆矩阵。

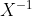但仅仅有方阵才有可能存在逆矩阵（不熟悉定理的同学建议去补补线性代数），因此能够通过左乘 使等式变成 ，因此,有同学可能会有疑问不一定存在啊，确实是，可是极少不存在，后面会介绍不存在的处理方法，先别着急。如今你仅仅须要明确为什么就能够了。而且记住。

介绍完normal equation求解參数，我们已经知道了两种求解參数的方法。normal equation和梯度下降。如今来对照下这两种方法的优缺点以及什么场景选择什么方法。

详细见下表吧：

回到上面说的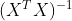不一定存在，这样的情况是极少存在的。假设不可逆了，一般要考虑一下两者情况：

（1） 移除冗余特征。一些特征存在线性依赖。

（2） 特征太多时，要删除一些特征。比如（m<n)，对于小样本数据使用正则化。