产生数

产生数这道题是一道很好的训练BFS和DFS的题，由于我是一个萌新，且正在学习DFS（深度优先搜索），我便把我的DFS代码展示出来，以供各位萌新学习。如果各位大佬有更好的DFS做法，欢迎向我提出建议。

产生数

 

描述

 

给出一个整数n（n≤2000）和k个变换规则（k≤15）。规则：

① 1个数字可以变换成另1个数字；

② 规则中，右边的数字不能为零。

例如：n=234，k=2规则为

2 → 5

3 → 6

上面的整数234经过变换后可能产生出的整数为（包括原数）234，534，264，564共4种不同的产生数。

求经过任意次的变换（0次或多次），能产生出多少个不同的整数。仅要求输出不同整数个数。

 

输入

n

k

x₁ y₁

x₂ y₂

... ...

x_n y_n

输出

输出满足条件的整数个数。

输入样例 1 

234
2
2 5
3 6

输出样例1

4

 

 

首先，我们要知道一个数学公式：满足条件的个数之和=（每位数字的可变化次数+1）相乘；

如234，1，2->5；则个位数字的可变化次数=0，十位数字的可变化次数=0，百位数字的可变化次数=1；所以满足条件的个数之和=（0+1）*（0+1）*（1+1）=2；

懂得了这一点，这道题就基本上完成了一半了，然后就是写代码：

这是我最先的代码：

这种做法爆了3个点，经过我思考后，对代码进行了一些修改，如下：

#include<bits/stdc++.h>
using namespace std;
int a[15],b[15],c[4],error[10];
//a,b分别为规则中x1，y1，c为n的各位数字，error为统计重复出现的数字
int n,m,tot,tmp,ans=1;
//n为最初的三位数，m为规则个数，tot统计每位可变化次数，tmp用来统计无效位数，ans用来记录答案
//void f(int p)
//{
//    for(int j=0;j<m;j++)//从每个规则中寻找符合的
//    {
//        if(p==a[j])
//        {
//            tot++;
//            if(error[p]!=0)//避免无限调用f函数，如果重复则不调用
//            {
//                for(int i=0;i<9;i++)
//                {
//                    if(error[i]!=0)
//                    {
//                        tot--;
//                        error[i]=0;//清空数组
//                    }
//                }
//            }
//            else
//            {
//                error[p]=p;//统计重复出现
//                f(b[j]);//递归调用
//            }
//        }
//    }
//}
//void dfs()
//{
//    for(int i=0;i<(4-tmp);i++)
//    {
//        f(c[i]);//调用f函数查找某位数数字的可变化次数
//        ans=ans*(tot+1);//满足条件的个数之和
//        tot=0;//清除当前位数的统计信息，为统计下一位做铺垫
//    } 
//}
//int main()
//{
//    cin>>n>>m;//输入
//    for(int i=0,j=1000;i<4;i++,j/=10)
//    {
//        if(tmp==i&&n/j==0)//统计无效位数
//        {
//            tmp++;
//        }
//        else
//        {
//            c[i-tmp]=n/j%10;//提取各个位数上的数字
//        }
//    }
//    for(int i=0;i<m;i++)
//    {
//        cin>>a[i]>>b[i];//输入
//    }
//    dfs();//调用
//    cout<<ans;
//    return 0;
//}
void dfs(int p)
{
    error[p] = 1;//打标记 
    tot++;//相当于最后的+1
    for(int j = 0; j < m; j++)//从每个规则中寻找符合的
    {
        if(a[j]==p)
        {
            if(error[b[j]]==0)//避免无限调用f函数，如果重复则不调用
            {
                f(b[j]);
            }
        }
    }
}
int main()
{
    cin>>n>>m;
    for(int i=0,j=1000;i<4;i++,j/=10)
    {
        if(tmp==i&&n/j==0)
        {
            tmp++;//统计无效位数
        }
        else
        {
            c[i-tmp]=n/j%10;//提取各个位数上的数字
        }
    }
    for(int i=0;i<m;i++)
    {
        cin>>a[i]>>b[i];
    }
    for(int i=0;i<(4-tmp);i++)
    {
        dfs(c[i]);
        ans *= tot;
        // 当前位清理统计信息，为下一次统计做准备 
        tot=0;
        for(int j = 0; j <= 9; j++) error[j] = 0;//清空数组
    }
    cout<<ans;
    return 0;
}

这是我老师的做法，思路相同，但写法不一样：

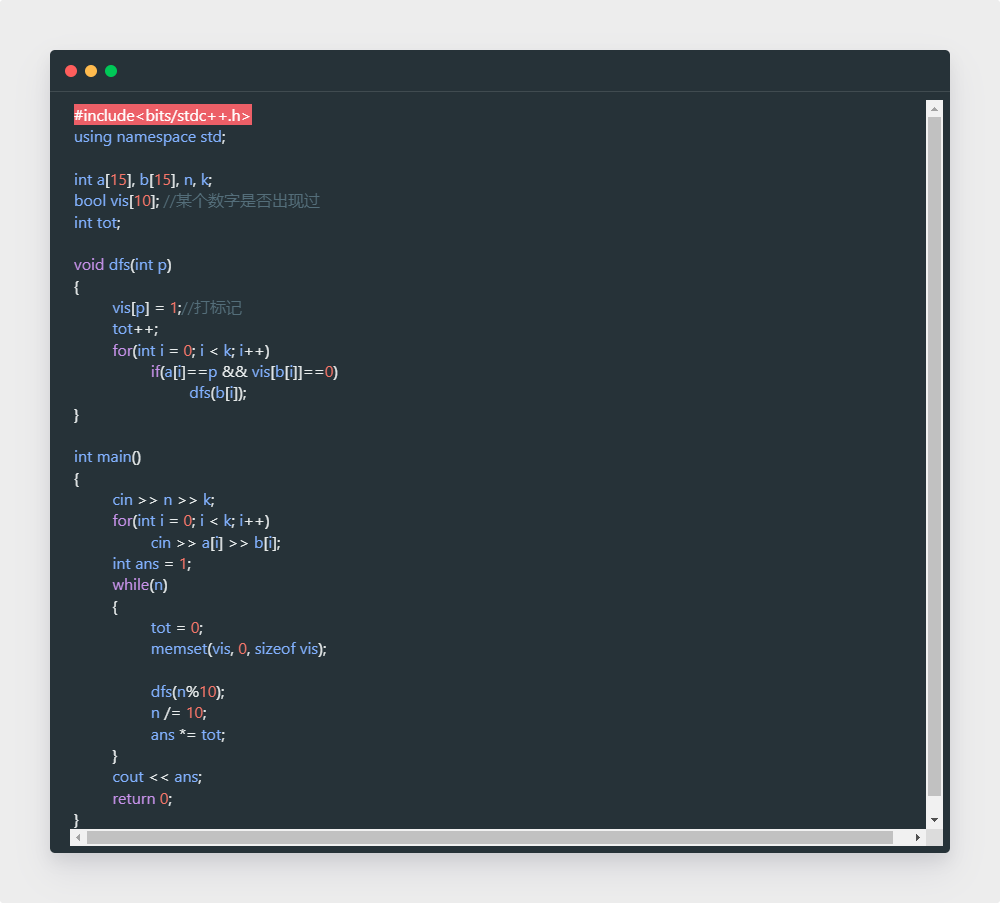
其中作用是把vis数组清空，作用详见https://www.csdn.net/gather_27/MtjakgwsNzYtYmxvZwO0O0OO0O0O.html