一种计算大数阶乘的算法

在很多C/C++的书上，都给出了两种阶乘的计算方法，一种为利用递归进行计算；一种利用阶乘的定义进行计算。下面给出这两种算法的C程序源代码。

1. 利用阶乘的定义进行计算：

  1: unsigned long factorial( int n )
  2: {
  3:     if( n == 0 )
  4:         return 1;
  5:     unsigned long result = 1;
  6:     for( int i = 1; i < n + 1; ++i )
  7:     {
  8:         result *= i;
  9:     }
 10:     return result;
 11: }

2. 利用递归进行计算：

  1: unsigned long factorial( unsigned long n )
  2: {
  3:     unsigned long result = 0;
  4:     if( n == 0 )
  5:         return 1;
  6:     else
  7:         result = n*factorial( n-1 );
  8:     return result;
  9: }

但是，由于阶乘的结果随着n的增大将急剧增加。最终导致即使是unsigned long类型的整数也无法保存计算结果。那么，这时候，我们应该怎么办呢？

现在，我们就要介绍一种计算方法，该方法的主要思路如下：

1.开辟一个大小为10000或更大的整形数组；

2.数组的每一个元素只保存计算结果中的一位数字，数组索引最小的元素对应计算结果的最小位，依次类推；

3.在计算中，将1-n中的每一个数字都与数组中的每一个数相乘，将与某元素的乘积仍保存在该元素中；

4.在1-n中的每个数字与所有元素做完乘积之后，依次每一个元素中的数字是否超过10（或者radix），若超过，则向前进位；

按照上面所描述的算法，我们在这里利用C++语言进行了实现：

  1: #include <iostream>
  2: #include <sstream>
  3: 
  4: #define s_int short int
  5: #define MAXDIGIT 50000
  6: #define RADIX 10
  7: 
  8: using std::cout;
  9: using std::endl;
 10: using std::cin;
 11: 
 12: //实现进位
 13: bool carry( s_int result[], int &dgts )
 14: {
 15:     int i;
 16:     s_int carry_value = 0;
 17:     for( i = 0; i < dgts; i++ )
 18:     {
 19:         result[i] += carry_value;
 20:         carry_value = ( result[i] < RADIX ) ? 0 : ( result[i] / RADIX );
 21:         result[i] -= carry_value * RADIX;
 22:     }
 23: 
 24:     //处理最后一位：
 25:     //若需进位，则循环进位，直到不需进位为止
 26:     result[i] += carry_value;
 27:     while( result[i] >= RADIX && i < MAXDIGIT )
 28:     {
 29:         carry_value = result[i] / RADIX;
 30:         result[i] -= carry_value * RADIX;
 31:         result[++i] = carry_value;
 32:         ++dgts;
 33:     }
 34: 
 35:     if( i >= MAXDIGIT )
 36:         return false;
 37: 
 38:     return true;
 39: }
 40: 
 41: //
 42: // The function return the total digits of the result.
 43: //
 44: int factorial( int n, s_int result[] )
 45: {
 46:     memset(result, 0, sizeof(s_int)*MAXDIGIT);
 47:     int digits = 0;
 48:     result[0] = 1;
 49: 
 50:     // 0! = 1
 51:     if( n == 0 ) return 1;
 52:     
 53:     for( int i = 2; i < n+1; ++i )
 54:     {
 55:         for( int j = 0; j <= digits; ++j )
 56:         {
 57:             result[j] *= i;
 58:         }
 59:         if( !carry( result, digits ) )
 60:             break;
 61:     }
 62: 
 63:     return digits >= MAXDIGIT ? -1 : digits;
 64: }
 65: 
 66: void print( s_int result[], const int &digits )
 67: {
 68:     if( digits < 10 )
 69:         for( int i = digits; i >= 0; i-- )
 70:             cout << result[i];
 71:     else
 72:     {
 73:         cout << result[digits] <<".";
 74:         for( int i = digits -1; i >= 0; i-- )
 75:             cout << result[i];
 76:         cout << "E" << digits;
 77:     }
 78:     cout << endl;
 79: }
 80: 
 81: int main(void)
 82: {
 83:     s_int result[MAXDIGIT];
 84:     int n;
 85:     int digits;
 86: 
 87:     cout << "Input the value of n: ";
 88:     cin >> n;
 89:     
 90:     if( n < 0 )
 91:     {
 92:         cout << "Error: A positive integer is need!" << endl;
 93:         return 0;
 94:     }
 95: 
 96:     if( (digits = factorial(n, result)) == -1 )
 97:     {
 98:         cout << "Error: Overflow!" << endl;
 99:         return 0;
100:     }
101:     else
102:     {
103:         print(result, digits);
104:         return 0;
105:     }
106: }

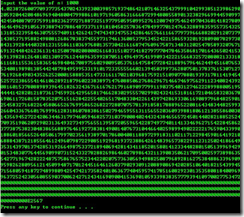
对1000！进行计算，计算结果如图：