「学习笔记」SOS DP

SOS DP 学习笔记

0.0 前言

本文大部分译自 CF 博客上的原文。Link here

0.1 前置知识

• 状压 DP

1.0 简介

SOS DP，全称 Sum over Subsets dynamic programming，意为子集和 DP，用来解决一些涉及子集和计算的问题。

1.1 例题引入

给定一个含 $2^N$ 个整数的集合 A，我们需要计算：对于每个集合 $x\in A$，求 $x$ 中所有元素 $i$ 的 $A[i]$ 的和，即求：

$\begin{gather*}{F[sta]=\sum\limits_{i\subseteq sta} A[i]}\end{gather*}$

1.2 解决方案

1.2.1 朴素算法

直接按照题意模拟即可，复杂度为 $O(4^N)​$。

for(int sta=0;sta<(1<<N);sta++)
  	for(int i=0;i<(1<<N);i++)
      	if((sta&i)==i)F[sta]+=A[i];

1.2.2 枚举子集

对于每个状态，我们只遍历它的子集而去除了无关状态。如果一个状态的二进制位上只有 $k$ 个 $1$，我们只需枚举它的 $2^k$ 个子集。这样的状态一共有 $\dbinom{N}{k}$ 个，因此总迭代次数 $=\sum\limits_{k=0}^N{\dbinom{N}{k}2^k}=(1+2)^N=3^N$，时间复杂度即为 $O(3^N)$。

for(int sta=0;sta<(1<<N);sta++)
{
    F[sta]=A[0];
	for(int i=sta;i>0;i=(i-1)&sta)
		F[sta]+=A[i];
}

1.2.3 SOS DP

上面枚举子集的方法有明显的缺陷：当一个状态的二进制位上有 $k$ 个 $0$ 时，它将在其他（不包含本身）状态迭代时被访问 $2^k-1$ 次，存在重复的计算。

而产生这种现象的原因就是：我们没有在 $A[x]$ 被不同 $F[sta]$ 利用时建立一定的联系。我们应添加另一个状态来避免上述的重复计算。

定义状态 $S(sta)=\{x|x\subseteq sta\}$。现在我们把这个集合划分为不相交的组。

$S(sta,i)=\{x|x\subseteq sta \&\& sta\oplus x<2^{i+1}\}$。我们将二进制位数从 $0$ 开始从低位向高位表示，那集合 $S(sta,i)$ 就表示只有第 $i$ 位以及更低位与 $sta$ 不同的 $x$ 的集合。

举个例子：$S($1011010$,3)=\{$1011010$,$1010010$,$1011000$,$1010000$\}$ 。其中 $sta$ 中的 1010 即为 $sta$ 的第 $3$ 至第 $0$ 位，集合中的元素的加粗部分都与 $sta$ 保持一致。

让我们尝试将 $sta$ 与 $x$ 建立联系。

1. $sta$ 的第 $i$ 位是 $0$。

   显而易见地，$sta$ 与 $x$ 的第 $i$ 位均为 $0$。因此 $x$ 仅有 $0$ 至 $i-1$ 位与 $sta$ 不同，故有 $S(sta,i)=S(sta,i-1)$。

2. $sta$ 的第 $i$ 位是 $1$。

   那么 $S(sta,i)$ 就有两部分组成：

   第一部分：$x$ 的第 $i$ 位为 $0$，即为 $S(sta\oplus 2^i,i-1)$。

   第二部分：$x$ 的第 $i$ 位为 $1$，即为 $S(sta,i-1)$。

下图描述了如何将 $S(sta,i)$ 集合相互关联。任何集合 $S(sta,i)$ 的元素都是其子树中的叶子。$\color{red}{红色}$前缀表示的这一部分对其所有子结点都是公共的，而$\color{black}{黑色}$部分允许不同。

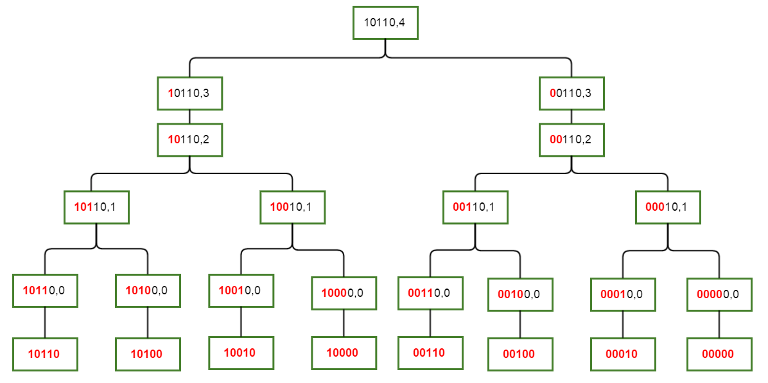
请注意，这些关系形成一个有向无环图，而不一定是有根树（请考虑当 $sta$ 不同但 $i$ 相同时）

在实现了这些关系之后，我们可以很容易地写出相应的动态规划。

for(int sta=0;sta<(1<<N);sta++)
{
    dp[sta][-1]=A[sta];// 叶结点
	for(int i=0;i<N;i++)
	{
		if(sta&(1<<i))
			dp[sta][i]=dp[sta][i-1]+dp[sta^(1<<i)][i-1];
		else dp[sta][i]=dp[sta][i-1];
	}
	F[sta]=dp[sta][N-1];
}

上述的算法浪费了较多空间，注意到每次 $i$ 这一维都由 $i-1$ 转移而来，因此可以采取滚动数组的方式优化空间。

for(int i=0;i<(1<<N);i++)
	F[i]=A[i];
for(int i=0;i<N;i++)
	for(int sta=(1<<N)-1;sta>=0;sta--)
	    if(sta&(1<<i))
			F[sta]+=F[sta^(1<<i)];

值得注意的是，在此处 $sta$ 这一维可以采用正序枚举的方式。

原因：……

上述算法的时间复杂度即为 $O(N·2^N)$。

1.3 应用范围

其实 sosdp 不仅可以求子集和，还可以求超集和。

超集和的核心代码如下：

for(int i=0;i<N;i++)
	for(int sta=(1<<N)-1;sta>=0;sta--)
	    if(!(sta&(1<<i)))
			F[sta]+=F[sta^(1<<i)];

细心的读者会注意到，求子集和与求超集和之间的区别仅差一个 !。

如何理解呢？这相当于我们把二进制中的每一个 $1$ 当作 $0$ 看待，$0$ 当作 $1$ 看待。比如 $sta=(1001)_2,i=2$，那 $F[(1001)_2]$ 就会从 $F[(1101)_2]$ 转移而来。而 $sta$ 为 $(1101)_2$ 的子集，$(1101)_2$ 为 $sta$ 的超集。

2.0 推荐习题

我在 vjudge 上组了一个题单，大家可以去练习一下。

点击此处 密码为 sosdpiseasyforme

2.1 习题简析

2.1.1 A - Compatible Numbers

题意简述

给定 $n$ 的元素 $a_1\dots a_n$，求对于每个 $a_i$ 是否存在 $a_j$ 满足 $i\ne j$ 且 $a_i\& a_j=0$，并输出 $a_j$。

数据范围：$1\le n\le10^6$，$1\le a_i\le 4\times 10^6$。

题目分析

sosdp 可以用来求子集和，而本题中满足条件的 $a_i$ 与 $a_j$ 不存在同一集合中。怎么办？想到将 $a_i$ 取反，取反后得到的数 $x$ 与 $a_j$ 的关系即为 $a_j\subseteq x$。在 dp 过程中将求和改为记录从谁转移而来，问题迎刃而解。

其实这道题本质上还是状压，如果将题目改为求个数，那才有 sosdp 的感觉。

代码展示

#include<bits/stdc++.h>
using namespace std;

const int M=1e6+5;

int all=(1<<22)-1;
int n,a[M],F[(1<<22)];

inline int read()
{
	int x=0,f=1;char ch;
	while(ch=getchar(),ch<48)if(ch==45)f=0;
	do x=(x<<1)+(x<<3)+(ch^48);
	while(ch=getchar(),ch>=48);
	return f?x:-x;
}

int main()
{
	memset(F,-1,sizeof(F));
	n=read();
	for(int i=1;i<=n;i++)
	{
		a[i]=read();
		F[a[i]]=a[i];
	}
	for(int sta=0;sta<=all;sta++)
	{
		if(F[sta]!=-1)continue;
		for(int i=0;i<22;i++)
			if(sta&(1<<i))
				if(F[sta^(1<<i)]!=-1)
				{
					F[sta]=F[sta^(1<<i)];
					break;
				}
	}
	for(int i=1;i<=n;i++)
	{
		int t=all&(~a[i]);
		printf("%d ",F[t]);
	}
	return 0;
}

---

2.1.2 B - Or Plus Max

题意简述

给定 $2^n$ 个数：$a_0,a_1,\dots,a_{2^n−1}$。对于 $1\le k\le 2^n−1$，求 $a_i+a_j$ 的最大值，同时满足 $i|j\le k$。

数据范围：$1\le n\le 18$，$1\le a_i\le 10^9$。

题目分析

此题需要我们对问题进行转化。

我们先对每个 $k$ 求出满足 $i|j=k$ 的 $a_i+a_j$ 的最大值，然后对答案求前缀最大值即可。但仍难以处理。

换一种求法，对于每个 $k$ 求出 $i|j\subseteq k$ 的 $a_i+a_j$ 的最大值，然后求前缀最大值。对状态 $F[k]$ 维护单个元素的最大值和次大值。

套上 sosdp，每次转移时注意一下合并时最大值和次大值的变化。还需注意 $F[k]$ 的初值为 $(a[k],-inf)$。

代码展示

#include<bits/stdc++.h>
#define FM first
#define SM second
using namespace std;

typedef pair<int,int> pii;
const int inf=1e9+1;
const int M=(1<<18);

int n,a[M],ans;
pii F[M];

inline int read()
{
	int x=0,f=1;char ch;
	while(ch=getchar(),ch<48)if(ch==45)f=0;
	do x=(x<<1)+(x<<3)+(ch^48);
	while(ch=getchar(),ch>=48);
	return f?x:-x;
}
pii Merge(pii A,pii B)
{
	if(A.FM<B.FM)swap(A,B);
	if(B.FM>A.SM)A.SM=B.FM;
    return A;
}

int main()
{
	n=read();
	for(int i=0;i<(1<<n);i++)
	{
		a[i]=read();
		F[i]=make_pair(a[i],-inf);
	}
	for(int i=0;i<n;i++)
		for(int sta=(1<<n)-1;sta>=0;sta--)
			if(sta&(1<<i))
				F[sta]=Merge(F[sta],F[sta^(1<<i)]);
	for(int i=1;i<(1<<n);i++)
	{
		int fi=F[i].FM,se=F[i].SM;
		ans=max(ans,fi+se);
		printf("%d\n",ans);
	}
	return 0;
}

---

2.1.3 C - Bits And Pieces

题意简述

给定 $n$ 个元素 $a_1\dots a_n$，对于每个三元组 $(i,j,k)$，找出 $\mathrm{max(a_i|(a_j\&a_k))}$，其中 $i<j<k$。

数据范围：$3\le n\le10^6$，$0\le a_i\le 2\times 10^6$。

题目分析