CF509C 题解

CF509C 题解

题目传送门

---

题目简述

定义两个长度为 \(n\) 的序列 \(a\) 和 \(b\)，\(a\) 序列中元素严格单调递增且均为正整数，\(b\) 序列中 \(b_i\) 等于 \(a_i\) 各个数位上的数之和。现给出 \(b\) 序列，要求求出对应 \(a\) 序列，并使得 \(a_n\) 尽量地小。

---

题目分析

构造题。

采用贪心算法。使得 \(a_n\) 尽可能的小，首先 \(a_1\) 得尽可能的小。显然地，从右往左尽可能多填 \(9\)，当无法填时将剩余的数填入，这是 \(b_1\) 一定时 \(a_1\) 最小的填法。

我们将接下来数的填法转换为一个子问题：给定 \(x\) 和 \(y\)，找到最小的使得数 \(c\) 使得 \(c>y\) 且 \(c\) 各数位之和为 \(x\)。

用类似模拟的方法解决这一问题：

我们从右向左遍历 \(y\) 的数字，尝试增加或改变当前数字，使得总和为 \(x\)。如果我们将从右往左第 \(k+1\) 位上的数字增加，那么 \(c\) 就已经保证大于 \(y\) 了，因此第 \(1\) 至 \(k\) 位上可以填 \(0-9\) 任意一个数字，从而可以使这 \(k\) 位数字之和为 \(0-9k\) 间的任意数字。

我们对填的数进行分类讨论：

1. \(b_i>b_{i-1}\)。此时贪心所填得的 \(a_i\) 必然比 \(a_{i-1}\) 要大。因此直接采用如填 \(a_1\) 的方法填 \(a_i\) 即可。

2. \(b_i\le b_{i-1}\)。此时我们需要找到一个位置 \(m\)，使得 \(b_i>b_{i-1}-sum\)。\(sum\) 指 \(a_{i-1}\) 的第 \(1\) 至 \(m-1\) 位上的数字之和。如图：

   

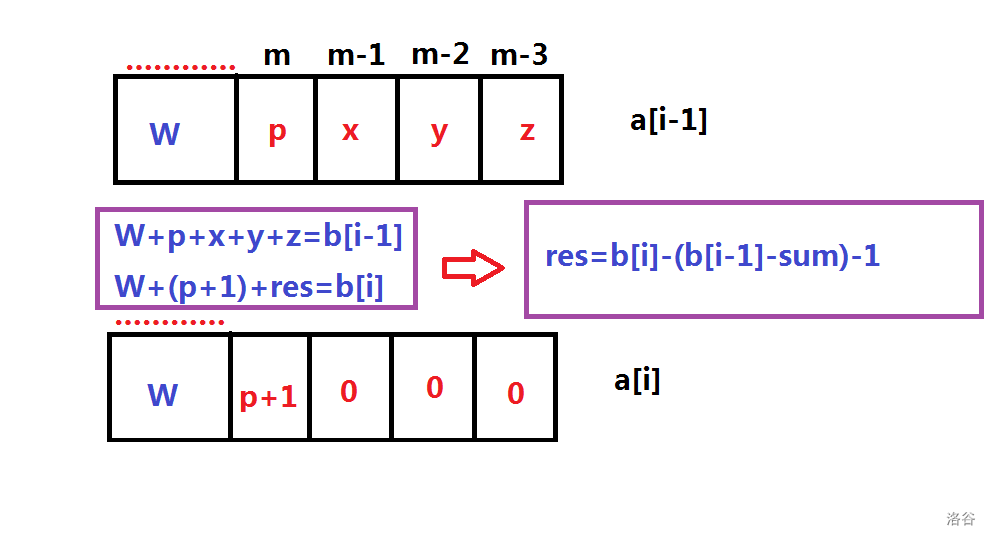
   从而我们可以在第 \(1\) 至 \(m-1\) 位上填上数字使其总和变为 \(res\)。此时我们就可以像情况 \(1\) 一样贪心地去填了。

   值得注意的是，当 \(b_i>b_{i-1}-x\)，但 \(a_{i-1}\) 的第 \(m\) 位上的数字 \(p\) 为 \(9\) 时，无法再加。此时我们就需要继续向高位找，同时将位上数字为 \(9\) 的变为 \(0\)，直到出现一个数字小于 \(9\) 为止。

在填的同时，注意 \(a_i\) 的长度随 \(i\) 的增大而单调不递减，因此 \(len\) 需要在每次处理完后更新。

讲了这么多，还是举个例子说说：

input:
2
18
18
output:
99
189

\(b_1=18\)，因此 \(a_1\) 最小为 \(99\)。而 \(b_2=b_1\)，属于情况 \(2\)，此时我们只需找到第 \(m\) 位使得第 \(1\) 至 \(m\) 位上的数之和 \(>b_{1}-b_{2}=0\)。当 \(m=2\) 时，发现 \(a_1\) 的第 \(2\) 位为 \(9\)，无法再加，因此我们将 \(m+1\)，发现 \(a_1\) 的第 \(3\) 位为 \(0\)，可以加上。因此我们在 \(a_2\) 的第 \(3\) 位填上一个 \(1\)，多余的数字等于 \(18-(18-18)-1=17\)。将 \(17\) 贪心地分在 \(2\) 个位置上，即为 \(89\)。因此 \(a_2=189\)。

再拿第 \(2\) 个样例来说：

\(b_1=3\)，因此 \(a_1\) 最小为 \(3\)。而 \(b_2=2<3\)，属于情况 \(2\)。找到第 \(2\) 位，填入一个 \(1\)，剩余数字为 \(2-(3-3)-1=1\)，填入第 \(1\) 位，因此 \(a_2=11\)。\(b_3=1<2\)，也属于情况 \(2\)。第 \(1\) 位时 \(x=0<1\)，第 \(2\) 位时 \(x=1=1\)，而第 \(3\) 位时 \(x=1+1>1\)，因此在第 \(3\) 位填入 \(1\)，剩余数字为 \(1-(2-2)-1=0\)，无需再补充。

---

代码展示

gota 函数，用于贪心地求出总和为 \(x\) 的最小正整数。注意到代码中 x-=9-c[++pos] 这一语句，即使在 \(x\) 不够减也没关系，循环结束后的一行 c[pos]+=x 可以将减多的 \(x\) 通过减少 \(c[pos]\) 来弥补。

void gota(int x)
{
	int pos=0;
	while(x>0)
	{
		x-=9-c[++pos];
		c[pos]=9;
	}
	c[pos]+=x;
	if(pos>len)len=pos;
}

核心求解部分。解释写在代码中应该更清晰一点。

for(int i=2;i<=n;i++)
{
	if(b[i]>b[i-1])// 情况一
		gota(b[i]-b[i-1]);
	else// 情况二
	{
		int dis=b[i]-b[i-1],pos=1;
      // 用dis表示差距，这需要通过把位上的数变为0来缩小。
		while(dis<=0||c[pos]==9)// 注意 dis>0 时也需满足 c[pos]!=9
			dis+=c[pos],c[pos++]=0;
		c[pos]++;// 在找到的位置+1
		gota(dis-1);// -1是因为上一行的+1
		if(pos>len)len=pos;
	}
	print(len);
}

---

总结

本题的讲解就到此结束了，语言措辞可能有些含糊，表述方式可能会有错误，如有疑问请您指正，谢谢。