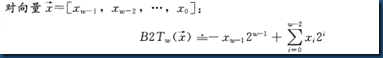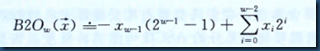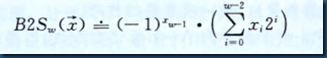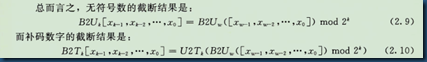深入理解计算机系统 - 信息的表示与处理
- 基础概念
- 整数的表示虽然只能编码一个相对较小的数值范围，但是这种表示是精确的；而浮点数虽然可以编码一个较大的数值范围，但是这种表示只是近似的。
- 由于表示的精度有限，浮点运算是不可结合的。
- 信息存储
- 字节是最小的可寻址的内存单元。内存可以看成一个非常大的字节数组，内存的每一个字节由唯一的数字来标识（地址）。所有可能地址的集合就是虚拟地址空间。
- c语言把每个指针和类型信息联系在了一起，指针的值表示某个对象的位置，而它的类型表示那个位置上所存储的对象的类型。
- 字长决定了虚拟空间的最大大小，一个字长为w位的机器，虚拟地址的范围是$0-2^w-1$，最多可访问$2^w$个字节。字长是指针数据的标称大小。
- 多字节对象被存储为连续的字节序列，对象的地址为所用字节的最小的地址。
- 小端法与大端法
- 在内存中从最低有效字节到最高有效字节顺序存放对象叫做小端法。
- 在内存中从最高有效字节到最低有效字节存放数据叫做大端法。
- 例如int型变量x位于ox100处，存放的数据为0x01234567，地址ox100~ox103的字节顺序依赖于机器的类型
- c语言中的移位运算
- 算术左移与逻辑左移一样，将x左移k位，是丢弃最高的k位，在最低的k位补0.移位运算是从左到右可结合的。x<<j<<k等价于(x<<j)<<k。
- 逻辑右移是在最高位补k个0，算术右移是在最高位补k个最高符号位。
- 几乎所有的编译器、机器组合都对有符号数进行算术右移，对于无符号数来说，右移必须是逻辑的。
- 当移位k大于数据的长度时，比如对整型变量x（4个字节32位）。x>>k，如果k大于32，那个实际位移量为k mod 32。
- 整数表示
- 补码编码
- 最高有效位$2_{w-1}$也称为符号位，它的权重为$-2^{w-1}$。
- 有符号数还有两种编码方式
- 反码。
- 除了最高有效位的权重为$-(2^{w-1}-1)$，其他和补码一致。
- 原码
- 最高有效位是符号位，用来决定剩下的位应该取负权还是正权。
- 原码变反码：符号位不变，其他位取反
- 原码变补码：符号位不变，其他位取反在加一。。
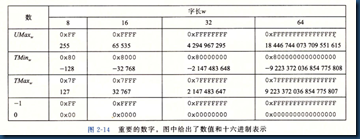
- 无符号数和有符号数进行转换时，强制转换的结果保持位值不变，只是改变了解释这些位的方式。比如-1映射到了$U_max$，$T_min$映射到了$T_max+1$。
- c语言在进行无符号数和有符号数运算时，是将有符号数转换成无符号数进行运算。
- 扩展一个数字的表示
- 无符号数进行零扩展。
- 有符号数进行符号扩展。
- 截断一个数字的方式时，直接去除截断的位数。
- 整数加法
- 无符号加法判断溢出：s=x+y。s<x或者s<y，则说明有溢出
- 补码加法
- 两个数的w位补码与无符号数加法有着相同的位级表示。
- x>0,y>0,x+y<=0说明发生了正溢出，x<0,y<0,x+y>=0说明发生了负溢出。
- $T_min$的相反数还是$T_min$
- 补码的非（相反数）
- -x与$\~x+1$的结果相同
- 乘法运算
- 无符号乘法 ：
- 补码乘法 : c语言中的有符号乘法通过将2w位的乘积截断为w位来实现的，将一个补码数截断为w位，相当于先计算该值模$2^w$，再将无符号数转换成有符号数。
- IEEE浮点表示
- IEEE754的浮点表示为$v=(-1)\*M\*2^E$。其中s为符号位，E为阶码，M为尾数。$E=e-bias$。其中bias为偏置，在32位的浮点数中，bias为-127（$2^k-1 – 1 k=8$），M为尾数位。$M=1+f$ f为小数。
- 当阶码E 为全0且尾数M 也为全0时，表示的真值x 为零，结合符号位S 为0或1，有正零和负零之分。当阶码E 为全1且尾数M为全0时，表示的真值x 为无穷大，结合符号位S 为0或1，也有+∞和-∞之分。
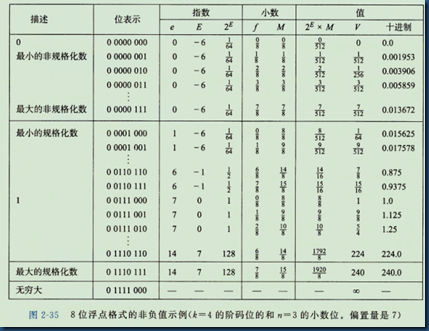
- 其中阶码全0表示非规格化数，全1用来表示无穷大和非数。对于规格化的数，$E=e-bias$，对于非规格化数$E=1-bias$。以8位浮点数为例，s=1,阶码位k=4,尾数位n=3。其偏置$bias =2^(k-1)-1 = 7 $。那么最小的规格化数为阶码为0001，尾数全0，表示的数为$1*2^(1-7)=\frac{1}{64}$。最大规格化数为阶码为1110，尾数全为1，表示的数为$1.111*2^(14-7）=\frac{15}{8}*2^7=240$。所以规格化数的范围为$\frac{1}{64}-240$。对于非规格化数，指数为$1-bias=-6$，最小的非规格化数，尾数最小为001。表示的值为$0.001*2^(-6)=\frac{1}{8}*\frac{1}{64}=\frac{1}{512}$。最大的非规格化数，其尾数位111。表示的值为$0.111*2^(-6)=\frac{7}{8}*\frac{1}{64}=\frac{7}{512}$，所以非规格化数的范围为$\frac{1}{512}-\frac{7}{512}$。可以看出非规格化数与规格化数是平滑详解的，这也是为什么非规格化数的阶码选择$1-bias$的原因。最大的规格化数为240，超出这个值会溢出到无穷大。
- 浮点运算缺乏结合性和分配性
- 当进行舍入时，会向最接近的值舍入，如果处于正中间，则默认向偶数舍入。
