微积分A(1)复习笔记
哪些点是坐标,哪些点是横坐标
驻点、极值点、零点是横坐标。
拐点是坐标。
不定积分-三角函数
\(\int \sin x\text dx=-\cos x+C\)
\(\int \cos x\text dx=\sin x+C\)
\(\int \tan x\text dx=-\ln|\cos x|+C\)
\(\int \cot x\text dx=\ln|\sin x|+C\)
\(\int \csc x\text dx=\ln|\csc x-\cot x|+C\)
\(\int \sec x\text dx=\ln|\sec x+\tan x|+C\)
\(\int \sin^2x\text dx=\frac x2-\frac{\sin 2x}4+C\)
\(\int \cos^2x\text dx=\frac x2+\frac{\sin 2x}4+C\)
\(\int \tan^2x\text dx=\tan x-x+C\)
\(\int \cot^2x\text dx=-\cot x-x+C\)
\(\int \csc^2x\text dx=-\cot x+C\)
\(\int \sec^2x\text dx=\tan+C\)
\(\int \sec x\tan x\text dx=\sec x+C\)
\(\int \csc x\cot x\text dx=-\csc x+C\)
\(\int e^{ax}\cos bx\ \text dx=\frac{1}{a^2+b^2}e^{ax}(b\sin bx+a\cos bx)+C\)
\(\int e^{ax}\sin bx\ \text dx=\frac{1}{a^2+b^2}e^{ax}(a\sin bx-b\cos bx)+C\)
不定积分-\(x^2a^2\)
以下默认 \(a>0\)
\(\int \sqrt{x^2+a^2}\text dx\) 用分部积分,前面补 \(x\)。
\(\int \frac 1{\sqrt{x^2+a^2}}\text dx=\ln(x+\sqrt{x^2+a^2})+C\)
\(\int \frac 1{x^2+a^2}\text dx=\frac 1a\arctan\frac xa+C\)
\(\int \sqrt{x^2-a^2}\text dx\) 也是分部积分,前面补 \(x\)。
\(\int \frac 1{\sqrt{x^2-a^2}}\text dx=\ln|x+\sqrt{x^2-a^2}|+C\)
\(\int \frac 1{x^2-a^2}\text dx=\frac 1{2a}\ln|\frac{x-a}{x+a}|+C\)
\(\int \sqrt{a^2-x^2}\text dx=\frac {a^2}2\arcsin\frac{x}a+\frac x2\sqrt{a^2-x^2}+C\)
\(\int \frac{1}{\sqrt{a^2-x^2}}\text dx=\arcsin\frac{x}{a}+C\)
\(\int \frac{1}{a^2-x^2}\text dx=\frac{1}{2a}\ln|\frac{x+a}{x-a}|+C\)
积化和差&和差化积
\(\sin x\sin y=-\frac 12[\cos(x+y)-\cos(x-y)]\)
\(\cos x\cos y=\frac 12[\cos(x+y)+\cos(x-y)]\)
\(\sin x\cos y=\frac 12[\sin(x+y)+\sin(x-y)]\)
\(\sin x+\sin y=2\sin\frac{x+y}2\cos\frac{x-y}2\)
\(\cos x+\cos y=2\cos\frac{x+y}2\cos\frac{x-y}2\)
\(\cos x-\cos y=-2\sin\frac{x+y}2\sin\frac{x-y}2\)
定积分
1.设 \(f(x)\) 为连续函数,则:\(\int_a^bf(x)\text dx=\int_a^bf(a+b-x)\text dx\)
2.\(\int_0^\frac\pi 2\sin^nx=\int_0^\frac\pi 2\cos^nx=A\)
若 \(n>1\) 且 \(n\) 为奇数,则 \(A=\frac{n-1}{n}\times\frac{n-3}{n-2}\times\cdots\times\frac 23\)。
若 \(n>1\) 且 \(n\) 为偶数,则 \(A=\frac{n-1}{n}\times\frac{n-3}{n-2}\times\cdots\times\frac 12\times \frac \pi 2\)
有理函数积分-多项式除法
先拆成一大堆 \(\frac{A}{(x-a)^k},\frac{Ax+B}{[(x+a)^2+b^2]^k}\) 的和
\(\int\frac{\text dx}{x-a}=\ln|x-a|+C\)
\(\int\frac{\text dx}{(x-a)^k}=-\frac{1}{k-1}\frac{1}{(x-a)^{k-1}}+C(k\ge 2)\)
\(\int\frac{x+a}{[(x+a)^2+b^2]^k}\text dx=\frac{-1}{2(k-1)[(x+a)^2+b^2]^{k-1}}+C(k\ge 2)\)
\(\int\frac{1}{(x+a)^2+b^2}=\frac{1}b\arctan(\frac{x+a}b)+C\)
\(\int\frac 1{[(x+a)^2+b^2]^2}=\frac 1{2b^2}[(x+a)[(x+a)^2+b^2]^{-1}+\frac{1}b\arctan(\frac{x+a}b)]+C\)
其中 \(a=0,b=1\) 的特殊情况:\(ans=\frac12[\frac{x}{x^2+1}+\arctan x]+C\)
有理函数积分-三角函数
万能代换:令 \(t=\tan\frac x2\),则 \(\sin x=\frac{2t}{1+t^2},\cos x=\frac{1-t^2}{1+t^2},dx=\frac{2\text dt}{1+t^2}\)
不可积的函数
\(e^{-x^2},\sin(x^2),\cos(x^2),\frac{\sin x}{x},\frac{\cos x}{x},\frac 1{\ln x},\sqrt{1-k^2\sin^2x}\)
积分的几何运用
1.平面区域面积
正常版本:\(S=\int_a^bf(x)\text dx\)
参数版本:\(S=\int_a^by(t)x'(t)\text dt\)
极坐标版本:\(S=\frac 12\int_{\alpha}^\betaρ(\theta)^2\text dθ\)
2.曲线弧长
正常版本:\(L=\int_a^b\sqrt{1+(f'(x))^2}\text dx\)
参数版本:\(L=\int_a^b\sqrt{(x'(t))^2+(y'(t))^2}\text dt\)
极坐标版本:\(L=\int_\alpha^\beta\sqrt{ρ(\theta)^2+(ρ'(\theta))^2}\text d\theta\)
3.曲率(据说它不考了)
曲线在 \(M(x(t),y(t))\) 处的曲率:
正常版本:
极坐标版本
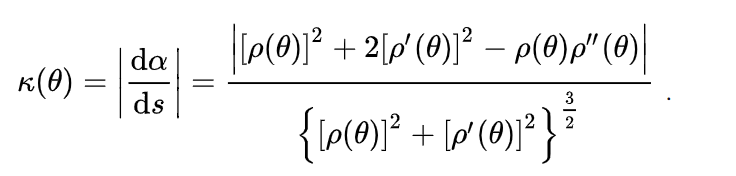
4.旋转体体积(绕 \(x\) 轴转一圈)
正常版本:\(V=\pi\int_a^bf(x)^2\text dx\)
参数版本:\(V=\pi\int_a^by(t)^2x'(t)\text dt\)
极坐标版本:\(V=\frac 23\pi\int_\alpha^\betaρ(\theta)^3\sin\theta\text d\theta\)
5.旋转体表面积(还是绕 \(x\) 轴转一圈)
所有版本等于弧长乘 \(2\pi |y|\) 或者 \(2\pi|ρ|\)。
广义积分的敛散性
\(\int_0^1\frac{1}{x^p}\text dx\) 和 \(\int_0^1\frac{\ln x}{x^p}\text dx\) 在 \(p<1\) 时收敛。
\(\int_1^{+\infty}\frac{1}{x^p}\text dx\) 和 \(\int_1^{+\infty}\frac{\ln x}{x^p}\text dx\) 在 \(p>1\) 时收敛。
\(\frac{1}{n+1}<\ln(1+\frac 1n)<\frac 1n\)。
\(\int_0^{+\infty}\frac{\sin x}{x^\alpha}\) 收敛当且仅当 \(0<\alpha<2\),绝对收敛当且仅当 \(1<\alpha<2\)。
\(\int_0^{+\infty}\frac{\sin x}{x^\alpha}\) 和 \(\int_0^{+\infty}\frac{\cos x}{x^\alpha}\) 在 \(0\) 处的收敛性是不一样的,\(\sin x\) 用 \(x\) 替换,\(\cos x\) 直接就有界了,扔掉就行了。
\(\int_0^{+\infty}\frac{\sin x}{x^\alpha}\) 和 \(\int_0^{+\infty}\frac{\cos x}{x^\alpha}\) 在 \(+\infty\) 处的收敛性一样,\(\alpha>1\) 时绝对收敛,\(\alpha\in(0,1]\) 条件收敛,\(\alpha\le 0\) 发散。
\(B(\alpha,\beta)=\int_0^1x^{\alpha-1}(1-x)^{\beta-1}\text dx\) 在 \(\alpha,\beta>0\) 时收敛。
\(\Gamma(\alpha)=\int_1^{+\infty}x^{\alpha-1}e^{-x}\text dx\) 在 \(\forall\alpha\) 收敛。
\(\Gamma(\alpha)=\int_0^{+\infty}x^{\alpha-1}e^{-x}\text dx\) 在 \(\alpha>0\) 时收敛。
常微分方程-一阶
1.先考虑能不能化简成 \(\frac{\text dy}{\text dx}=f(x)g(y)\) 的形式,然后两边直接积分。
2.不能的话,尝试一下令 \(u=p(x,y)\) 的换元,让它变成 \(u,x\) 的两边积分形式。
3.\(y'+p(x)y=q(x)\),注意是 \(y\),\(y^2\) 就不行。这里直接常数变易法。
4.\(y'+p(x)y=q(x)y^\alpha\),两边同除以 \(y^\alpha\) 之后令 \(z=y^{1-\alpha}\)。
常微分方程-二阶
1.一看就能降成一阶的,令 \(p=y'\)。
2.含 \(y,y',y''\),不含 \(x\) 的,令 \(p=y'\),则 \(y''=p\frac{\text dp}{\text dy}\),那么换掉式子中的 \(y''\) 就行了。
3.常系数齐次方程
写出特征方程,是第几个重复的,就在前面乘上几个 \(x\),第 \(0\) 个是 \(e^{\lambda x}\)。
你说 \(\lambda\) 是复数怎么办?\(e^{(a+bi)x}=e^{ax}\cos bx+ie^{ax}\sin bx\),把实部和虚部都写进去就行了,写正值。
这样可以求 \(n\) 个线性无关的解,就可以线性表出通解了。
4.常系数非齐次方程
想求通解,先求特解,然后用齐次的解线性表出。
怎么求特解?
首先是 \(f(x)=P_m(x)e^{\lambda x}\) 的情况,这时候判断一下 \(\lambda\) 是几重特征根。
设 \(y(x)=Q(x)e^{\lambda x}\),并将 \(y,y',y''\) 求出后代入 \(y''+ay'+by=P_m(x)e^{\lambda x}\) 可得:\(Q''+(2\lambda+a)Q'+(\lambda^2+a\lambda+b)Q=P_m(x)\)。
一重根的话,\(Q\) 的系数是 \(0\),二重根的话,\(Q',Q\) 的系数都是 \(0\)。
所以,不是根,设 \(Q\) 为 \(m\) 次多项式。一重根,设为 \(x\times Q_m(x)\),二重根就 \(x^2Q_m(x)\)。
注意这里 \(\lambda\) 是 \(f(x)\) 的已知指数,不是特征根。
然后你设完 \(Q\) 之后,在上式跟 \(P_m(x)\) 比较系数,就可以知道 \(Q\) 是啥了。
然后特解就求好了,通解的就看非齐次了。
你说 \(f(x)\) 不是 \(P_m(x)e^{\lambda x}\) 的形式怎么办?
\(f(x)=e^{ax}[P_m(x)\cos bx+P_n(x)\sin bx]\) 时,特解设为 \(y=e^{ax}[Q_1(x)\cos bx+Q_2(x)\sin bx]x^k\),其中 \(k\) 是 \(a+bi\) 的重数,\(Q_1,Q_2\) 是两个 \(\max(n,m)\) 次的多项式,待定系数。
5.不是常系数的二阶方程
标准形式:\(y''+a(x)y'+b(x)y=f(x)\)。
分两个情况,一个是已知齐次的一个特解,求非齐次的一个特解,另一个是已知齐次的两个线性无关解,求非齐次的通解。
情况1:设 \(y=cY\),其中 \(Y\) 是齐次特解。求出 \(Y,Y',Y''\) 并代入 标准形式 后,得 \(Yc''+(2Y'+aY)c'+(Y''+aY'+bY)c=f\)。\(c\) 的系数为 \(0\),就变成关于 \(c'\) 的一阶了。
情况2:设 \(Y=c_1y_1+c_2y_2\),然后 \(Y'=c_1y_1'+c_2y_2'+c_1'y_1+c_2'y_2=0\),令 \(c_1'y_1+c_2'y_2=0\),则 \(Y'=c_1y_1'+c_2y_2',Y''=c_1''y_1+c_2''y_2+c_1y_1'+c_2y_2'\)。
将 \(Y,Y',Y''\) 代入 标准形式,并利用 \(y_1,y_2\) 是齐次的解这一条件,可以得到 \(c_1'y_1'+c_2'y_2'=0\)。
联立即 \(c_1'y_1'+c_2'y_2=c_1'y_1+c_2'y_2=0\)。解方程组可得 \(c_1',c_2'\),还原就可以得到 \(c_1,c_2\) 和 \(Y\) 了。然后通解的话,就是加上 \(y_1,y_2\) 的线性组合。
6.欧拉方程
标准形式:\(\sum_{i=0}^nx^iy^{(i)}=f(x)\)。
令 \(t=\ln |x|\),然后
这样就可以把 \(y',y''\) 前面的 \(x,x^2\) 给消掉,变成含 \(y'',y',y,t\) 的式子。
注意到这里 \(y'',y',y\) 都是常系数,所以就同 常系数二阶方程 求解了。


