[校内训练]palace(点分治+启发式合并)
Description
给定一棵 \(n\) 个节点的树,每个节点有一个颜色 \(c_i\)。
要求选出两条不相交的路径 \((x,y),(u,v)\),满足 \(c_x=c_y\) 且 \(c_u=c_v\)。
\((x,y),(u,v)\) 和 \((u,v),(x,y)\) 算同一种方案。
求有多少种合法方案。
还有 \(m\) 个询问,第 \(i\) 次询问 \(k_i\) 不能作为路径端点的方案数。
方案数全部对 \(10^9+7\) 取模。
记颜色种类数为 \(q\),则 \(n,m,q\le10^5\)。
时空限制 \(\text{1s/512MB}\)。
Solution
考虑一种非常暴力的做法:
记 \(ans_x\) 表示 \(x\) 作为路径端点的合法方案数。
枚举路径 \((x,y)\),满足 \(c_x=c_y\),接下来算出和 \((x,y)\) 不相交的路径数 \(cnt\)。
然后把 \(ans_x,ans_y\) 都加上 \(cnt\)。
总合法方案数是 \(\frac{1}{4}\sum_{i=1}^nans_i\),因为一个方案包含 \(4\) 个互不相同的端点。
然而 \(n\le 10^5\),显然不能直接枚举 \(x,y\)。
考虑点分治,即设重心为 \(G\),算出经过点 \(G\) 的路径 \((x,y)\) 的贡献。
记 \(f[u]\) 表示以 \(G\) 为根时,\(u\) 的子树内有多少条端点同色的路径。
那么不和 \((x,y)\) 相交的同色路径数就是下图中绿色点的 \(f\) 之和:
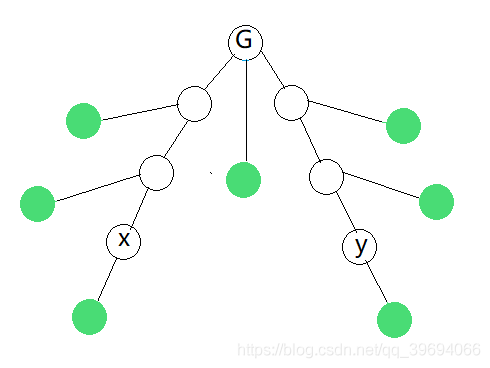
具体地,记 \(sum\) 为 \(G\) 所有子节点的 \(f\) 之和。
记 \(g[x]\) 为所有满足以下条件的点 \(v\) 的 \(f[v]\) 之和:
- 存在某个点 \(u\),使得 \(u\) 是路径 \((G,x)\) 上的点,且 \(u\) 与 \(v\) 有边。
- \(v\) 不是路径 \((G,x)\) 上的点。
- \(v\) 不是 \(G\) 的子节点。
令 \(G\) 的深度为 \(1\),记 \(h[x]\) 表示路径 \((G,x)\) 上深度为 \(2\) 的点的 \(f\) 值。
那么与 \((x,y)\) 不相交的路径数就是:\(sum-h[x]-h[y]+g[x]+g[y]\)。
其中 \(sum,g,h\) 均可 dfs 一遍得到。
至于 \(f\),我们可以在点分治之前,先以 \(1\) 为根。
对每个点 \(u\) 算出 \(f_{in}[u]\),表示 \(u\) 子树内同色路径数。再算出 \(f_{out}[u]\) 表示 \(u\) 子树外同色路径数,并记下此时 \(u\) 的父节点 \(fa[u]\)。
\(f_{in}[u]\) 和 \(f_{out}[u]\) 只和 \(u\) 子树内每种颜色的点数有关,可以启发式合并。
以 \(G\) 为根时,若 \(u\) 的父亲还是 \(fa[u]\),那么 \(f[u]=f_{in}[u]\),否则 \(f[u]=f_{out}[fa[u]]\)。
显然还是不能直接枚举 \(x,y\)。
考虑枚举 \(G\) 的子节点,即计算 \(G\) 的前 \(i-1\) 个子节点的子树对第 \(i\) 个子节点的子树中的点的贡献。然后再反过来计算后面的子树对前面的子树的贡献。
对于每个 \(y\),我们只要知道满足 \(c_x=c_y\) 的 \(x\) 的个数,以及 \(\sum h[x]-g[x]\),就可以计算对 \(ans_y\) 的贡献了。
那么我们记 \(C[i]\) 表示满足 \(c_x=i\) 的 \(x\) 的个数,记 \(S[i]\) 表示满足 \(c_x=i\) 的 \(\sum h[x]-g[x]\)。
枚举到一个 \(G\) 的子节点 \(z\) 的时候,先 dfs 一遍 \(z\) 的子树,用之前的 \(C,S\) 数组给子树内的点贡献,然后再 dfs 一遍 \(z\) 的子树,更新 \(C,S\) 数组。
时间复杂度 \(O(n\log n)\),空间复杂度 \(O(n)\)。
Code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
template <class t>
inline void read(t & res)
{
char ch;
while (ch = getchar(), !isdigit(ch));
res = ch ^ 48;
while (ch = getchar(), isdigit(ch))
res = res * 10 + (ch ^ 48);
}
template <class t>
inline void print(t x)
{
if (x > 9) print(x / 10);
putchar(x % 10 + 48);
}
const int e = 2e5 + 5, mod = 1e9 + 7;
int col[e], ans[e], n, m, q, adj[e], nxt[e], go[e], sze[e], son[e], num, inv4, fans;
int f[e], g[e], h[e], sum, G, tot, id[e], cnt[e], mx[e], now, c[e], s[e];
int f_in[e], f_out[e], fa[e], sub_f[e];
bool vis[e];
vector<int>ch;
inline void add(int &x, int y)
{
(x += y) >= mod && (x -= mod);
}
inline void del(int &x, int y)
{
(x -= y) < 0 && (x += mod);
}
inline int plu(int x, int y)
{
add(x, y);
return x;
}
inline int sub(int x, int y)
{
del(x, y);
return x;
}
inline int mul(int x, int y)
{
return (ll)x * y % mod;
}
inline int ksm(int x, int y)
{
int res = 1;
while (y)
{
if (y & 1) res = (ll)res * x % mod;
y >>= 1;
x = (ll)x * x % mod;
}
return res;
}
inline void link(int x, int y)
{
nxt[++num] = adj[x]; adj[x] = num; go[num] = y;
nxt[++num] = adj[y]; adj[y] = num; go[num] = x;
}
inline void dfs1(int u, int pa)
{
sze[u] = 1;
mx[u] = 0;
id[++tot] = u;
for (int i = adj[u]; i; i = nxt[i])
{
int v = go[i];
if (v == pa || vis[v]) continue;
dfs1(v, u);
sze[u] += sze[v];
mx[u] = max(mx[u], mx[v]);
}
}
inline void dfs2(int u, int pa)
{
sze[u] = 1;
fa[u] = pa;
for (int i = adj[u]; i; i = nxt[i])
{
int v = go[i];
if (v == pa) continue;
dfs2(v, u);
sze[u] += sze[v];
if (sze[v] > sze[son[u]]) son[u] = v;
}
}
inline int c2(int x)
{
return (ll)x * (x - 1) / 2 % mod;
}
inline void change(int x, int v)
{
del(now, c2(cnt[x]));
cnt[x] += v;
add(now, c2(cnt[x]));
}
inline void dfs4(int u, int pa, int op)
{
change(col[u], op);
for (int i = adj[u]; i; i = nxt[i])
{
int v = go[i];
if (v == pa) continue;
dfs4(v, u, op);
}
}
inline void dfs3(int u, int pa, bool keep, int op)
{
int i;
for (i = adj[u]; i; i = nxt[i])
{
int v = go[i];
if (v == pa || v == son[u]) continue;
dfs3(v, u, 0, op);
}
if (son[u]) dfs3(son[u], u, 1, op);
change(col[u], op);
for (i = adj[u]; i; i = nxt[i])
{
int v = go[i];
if (v == pa || v == son[u]) continue;
dfs4(v, u, op);
}
if (op == 1) f_in[u] = now;
else f_out[u] = now;
if (!keep) dfs4(u, pa, -op);
}
inline void dfs5(int u, int pa, int now_g, int now_h)
{
g[u] = now_g;
h[u] = now_h;
if (pa == G) ch.emplace_back(u);
int sum_f = 0, i;
for (i = adj[u]; i; i = nxt[i])
{
int v = go[i];
if (v == pa) continue;
if (fa[v] == u) f[v] = f_in[v];
else f[v] = f_out[u];
add(sum_f, f[v]);
}
for (i = adj[u]; i; i = nxt[i])
{
int v = go[i];
if (v == pa) continue;
if (u == G) add(sum, f[v]);
if (vis[v]) continue;
if (u == G) dfs5(v, u, 0, f[v]);
else dfs5(v, u, plu(now_g, sub(sum_f, f[v])), now_h);
}
for (i = adj[u]; i; i = nxt[i])
{
int v = go[i];
if (v == pa) continue;
add(g[u], f[v]);
}
}
inline void dfs6(int u, int pa, int op)
{
int x = col[u];
if (op == 1)
{
add(c[x], 1);
add(s[x], sub(g[u], h[u]));
}
else
{
add(ans[u], s[x]);
add(ans[u], mul(c[x], plu(sub(g[u], h[u]), sum)));
}
for (int i = adj[u]; i; i = nxt[i])
{
int v = go[i];
if (v == pa || vis[v]) continue;
dfs6(v, u, op);
}
}
inline void solve(int rt)
{
int i;
tot = now = sum = 0;
dfs1(rt, 0);
for (i = 1; i <= tot; i++)
{
int u = id[i], x = col[u];
g[u] = h[u] = s[x] = c[x] = 0;
if (max(mx[u], tot - sze[u]) * 2 <= tot) G = u;
}
ch.clear();
dfs5(G, 0, 0, 0);
g[G] = h[G] = 0;
int lenc = ch.size();
c[col[G]] = 1; s[col[G]] = 0;
for (i = 0; i < lenc; i++)
{
int v = ch[i];
dfs6(v, G, 2);
if (i != lenc - 1) dfs6(v, G, 1);
}
for (i = 1; i <= tot; i++) c[col[id[i]]] = s[col[id[i]]] = 0;
for (i = lenc - 1; i >= 0; i--)
{
int v = ch[i];
if (i != lenc - 1) dfs6(v, G, 2);
dfs6(v, G, 1);
}
add(ans[G], s[col[G]]);
add(ans[G], mul(c[col[G]], sum));
vis[G] = 1;
vector<int>sons = ch;
for (i = 0; i < lenc; i++) solve(sons[i]);
}
int main()
{
read(n); read(m); read(q);
int i, x, y;
for (i = 1; i <= n; i++) read(col[i]);
for (i = 1; i < n; i++) read(x), read(y), link(x, y);
dfs2(1, 0);
dfs3(1, 0, 0, 1);
for (i = 1; i <= n; i++) change(col[i], 1);
dfs3(1, 0, 1, -1);
solve(1);
for (i = 1; i <= n; i++) add(fans, ans[i]);
inv4 = ksm(4, mod - 2);
fans = mul(fans, inv4);
print(fans);
putchar('\n');
while (m--)
{
read(x);
print(sub(fans, ans[x]));
putchar('\n');
}
fclose(stdin);
fclose(stdout);
return 0;
}

