poj 2653 Pick-up sticks 线段相交
|
Description
Stan has n sticks of various length. He throws them one at a time on the floor in a random way. After finishing throwing, Stan tries to find the top sticks, that is these sticks such that there is no stick on top of them. Stan has noticed that the last thrown
stick is always on top but he wants to know all the sticks that are on top. Stan sticks are very, very thin such that their thickness can be neglected.
Input
Input consists of a number of cases. The data for each case start with 1 <= n <= 100000, the number of sticks for this case. The following n lines contain four numbers each, these numbers are the planar coordinates of the endpoints of one stick. The sticks
are listed in the order in which Stan has thrown them. You may assume that there are no more than 1000 top sticks. The input is ended by the case with n=0. This case should not be processed.
Output
For each input case, print one line of output listing the top sticks in the format given in the sample. The top sticks should be listed in order in which they were thrown.
The picture to the right below illustrates the first case from input. 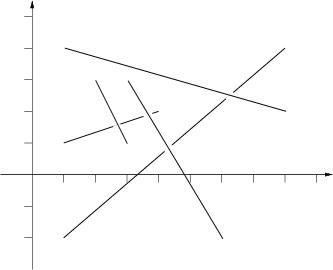 Sample Input 5 1 1 4 2 2 3 3 1 1 -2.0 8 4 1 4 8 2 3 3 6 -2.0 3 0 0 1 1 1 0 2 1 2 0 3 1 0 Sample Output Top sticks: 2, 4, 5. Top sticks: 1, 2, 3. Hint
Huge input,scanf is recommended.
Source |
--------------------
直接判断线段相交即可
--------------------
#include<vector>
#include<list>
#include<map>
#include<set>
#include<deque>
#include<queue>
#include<stack>
#include<bitset>
#include<algorithm>
#include<functional>
#include<numeric>
#include<utility>
#include<iostream>
#include<sstream>
#include<iomanip>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cctype>
#include<string>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<ctime>
#include<climits>
#include<complex>
#define mp make_pair
#define pb push_back
using namespace std;
const double eps=1e-8;
const double pi=acos(-1.0);
const double inf=1e20;
const int maxp=1111;
int dblcmp(double d)
{
if (fabs(d)<eps)return 0;
return d>eps?1:-1;
}
inline double sqr(double x){return x*x;}
struct point
{
double x,y;
point(){}
point(double _x,double _y):
x(_x),y(_y){};
void input()
{
scanf("%lf%lf",&x,&y);
}
void output()
{
printf("%.2f %.2f\n",x,y);
}
bool operator==(point a)const
{
return dblcmp(a.x-x)==0&&dblcmp(a.y-y)==0;
}
bool operator<(point a)const
{
return dblcmp(a.x-x)==0?dblcmp(y-a.y)<0:x<a.x;
}
double len()
{
return hypot(x,y);
}
double len2()
{
return x*x+y*y;
}
double distance(point p)
{
return hypot(x-p.x,y-p.y);
}
point add(point p)
{
return point(x+p.x,y+p.y);
}
point sub(point p)
{
return point(x-p.x,y-p.y);
}
point mul(double b)
{
return point(x*b,y*b);
}
point div(double b)
{
return point(x/b,y/b);
}
double dot(point p)
{
return x*p.x+y*p.y;
}
double det(point p)
{
return x*p.y-y*p.x;
}
};
struct line
{
point a,b;
line(){}
line(point _a,point _b)
{
a=_a;
b=_b;
}
bool operator==(line v)
{
return (a==v.a)&&(b==v.b);
}
void input()
{
a.input();
b.input();
}
double length()
{
return a.distance(b);
}
//2 规范相交
//1 非规范相交
//0 不相交
int segcrossseg(line v)
{
int d1=dblcmp(b.sub(a).det(v.a.sub(a)));
int d2=dblcmp(b.sub(a).det(v.b.sub(a)));
int d3=dblcmp(v.b.sub(v.a).det(a.sub(v.a)));
int d4=dblcmp(v.b.sub(v.a).det(b.sub(v.a)));
if ((d1^d2)==-2&&(d3^d4)==-2)return 2;
return (d1==0&&dblcmp(v.a.sub(a).dot(v.a.sub(b)))<=0||
d2==0&&dblcmp(v.b.sub(a).dot(v.b.sub(b)))<=0||
d3==0&&dblcmp(a.sub(v.a).dot(a.sub(v.b)))<=0||
d4==0&&dblcmp(b.sub(v.a).dot(b.sub(v.b)))<=0);
}
};
int n;
line a[110000];
bool v[110000];
int main()
{
while (~scanf("%d",&n))
{
if (n==0) break;
for (int i=1;i<=n;i++)
{
a[i].input();
}
for (int i=1;i<=n;i++)
{
for (int j=i+1;j<=n;j++)
{
if (a[i].segcrossseg(a[j])!=0)
{
v[i]=true;
break;
}
}
}
printf("Top sticks:");
int num=0;
for (int i=1;i<=n;i++)
{
if (!v[i])
{
if (!num) printf(" %d",i);
else printf(", %d",i);
num++;
}
else v[i]=false;
}
printf(".\n");
}
}





