⑨讲图论第三课: 图的邻接表表示法

每个链表的上边附设一个表头结点,在表头结点中,除了设有链域first用于指向链表中第一个结点之外,还设有存储顶点vi名或其它有关信息的数据域data 。
把同一个顶点发出的边链接在同一个边链表中,链表的每一个结点代表一条边,叫做表结点,结点中保存有与该边相关联的另一顶点的顶点下标 vertex 和指向同一链表中下一个表结点的指针 next。
在有向图的邻接表中,第 i 个边链表链接的边都是顶点 i 发出的边。也叫做出边表。
在有向图的逆邻接表中,第 i 个边链表链接的边都是进入顶点 i 的边。也叫做入边表。
邻接表的类型定义
#define nmax 100 /*假设顶点的最大数为100*/
typedef struct node *pointer;
struct node { /*表结点类型*/
int vertex ;
struct node *next ;
} nnode;
typedef struct {/*表头结点类型,即顶点表结点类型*/
datatype data ;
pointer first ;/*边表头指针*/
}headtype ;
typedef struct { /*表头结点向量,即顶点表*/
headtype adlist[nmax];
int n,e ;
}lkgraph ;
建立无向图邻接表的算法
void creatqraph(Ikgraph *ga)
{
/*建立无向图的邻接表*/
int i,j,e,k;
pointer p;
printf(“请输入顶点数:\n”);
scanf (“%d”, &(ga->n));
for (i =1; i<= ga->n; i++)
{
/*读入顶点信息,建立顶点表*/
scanf (“ \n %c”, &( ga->adlist[i].data) );
ga->adlist[i].first = NULL;
}
e = 0;
scanf (“\n%d,%d\n”, &i,&j ); /*读入一个顶点对号i和j*/
while (i>0)
{
/*读入顶点对号,建立边表*/
e++; /*累计边数 */
p = (pointer)malloc(size(struct node));/*生成新的邻接点序号为j的表结点*/
p-> vertex = j;
p->next = ga->adlist[i].first;
ga->adlist[i].first = p;/*将新表结点插入到顶点vi的边表的头部*/
p = (pointer)malloc(size(struct node));/*生成邻接点序号为i的表结点*/
p-> vertex = i;
p->next = ga->adlist[j].first;
ga->adlist[j].first=p; /*将新表结点插入到顶点vj的边表头部*/
scanf (“\n%d,%d\n”, &i,&j );/*读入一个顶点对号i和j*/
}
ga->e = e ;
}
该算法的时间复杂度是O(n+e)
在邻接表的边链表中,各个表结点的链入顺序任意,视表结点输入次序而定。
设图中有 n 个顶点,e 条边,则用邻接表表示无向图时,需要 n 个表头结点,2e 个表结点;用邻接表表示有向图时,若不考虑逆邻接表,只需 n 个表头结点,e 个表结点。
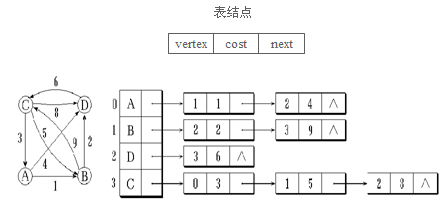
带权图的边结点中还应保存该边上的权值 cost。
网络 (带权图) 的邻接表
另外,图的邻接表可以用STL里的vector代替:vector<int>a[MAXSIZE];



