python 基于熵值法进行综合评价
在多指标的综合加权评价中,确定各项指标的权重是非常关键的环节。对各指标赋权的合理与否,直接关系到分析的结论。确定权重系数的方法很多,归纳起来分为两类:即主观赋权法和客观赋权法。主观赋权法是由评价人员根据各项指标的重要性而认为赋权的一种方法,充分反应专家的经验,目前,使用较多的是专家咨询法、层次分析法、循环打分法等。客观赋权法是从实际数据出发,利用指标值所反应的客观信息确定权重的一种方法,如熵值法、银子分析法、主成分分析、均方差法、相关系数法等。本文主要介绍熵值法进行综合评价,并使用Python进行实现。
1.赋权方法介绍
熵最早是一个物理热力学概念,是指在一定条件下对无序或随机变量计算不能做功的一种热能单位。通过这种测算方法,衍生出一种数学计算方法即熵值法,用以计算某些指标所反映出的权重,用来确定某些指标的离散性,从而对多种的指标数据进行综合性的评定和分析,进而确定其最具影响力的指标因素,为决策提供一定的参考依据。
熵值最早由申农(Shannon)将其引入信息论计算,信息是系统对有序数据的衡定,熵值是对不确定指标或无序指标的衡定,两者在结果互为相反数。由此,可以通过信息和熵的计算和分析得出,熵与信息的无序性构成正比例关系,和权重值构成成反比例关系。利用权重指标的变异程度的特性,可以计算并确定其指标权重的大小,从而能对研宄对象开展比较客观的评价。熵值法还能够在计算评定过程中剔除对整体评价影响不大的权重指标,能够更好地提高评价的准确性。
2.引入案例
设有以下模型,3层系统,15各原始指标,其中8个正向指标,6个负向指标,1个中性指标。使用熵值法进行赋权评价。

3.具体操作
1.数据标准化(归一化)
假设有m期数据,则设原始数据矩阵为X=(xi)m*n,其中m为样本容量n为指标个数,xij为第i个样本的第j个指标值。为了消除各指标的量纲、数量级及指标的正负取向有差异所带来的不可公度性,分析之前须将初始评价指标xij进行标准化。
对于正向指标处理:
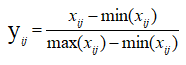
对于负向指标:
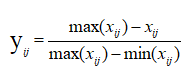
对于中性指标:
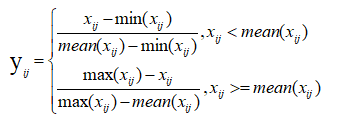
上式中,yij代表无量纲化后数据,经过无量纲化的数据都落到了[0,1]区间,yij值越大,说明评价结果越高。
2.非负平移处理
由于部分数据在无量纲化处理后为零或负值,为了便面在熵值求权数时取对数无意义,需要对数据进行处理。这里采取平移法。
zij=yij+1 (i=1,2,...m;j=1,2,...n)
3.求各指标在各方案下的比值
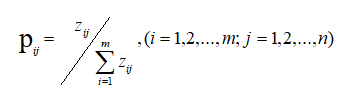
4.求各指标的信息熵
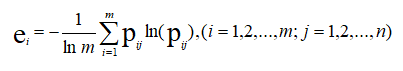
5.求各指标的效用
gj=1 - ej ,(j = 1,2,...,n)
6.求各指标权重
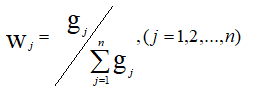
4.具体实现
4.1数据读取
df_src = pd.read_excel('data.xls', skiprows=1,dtype=object) df_src = df_src.set_index('date') df_src.index = pd.to_datetime(df_src.index, format='%Y%m%d').date # 正向指标 l_target_positive = ['x4','x5','x10','x11','x12','x13','x14','x15'] # 反向指标 l_target_negative = ['x1','x3','x6','x7','x8','x9'] # 中性指标 l_target_middle = ['x2'] l_target_economy = ['x1','x2','x3','x4'] # r1指标 l_target_finance = ['x5','x6','x7'] # r2指标 l_target_self = ['x8','x9','x10','x11','x12','x13','x14','x15'] # r3指标
4.2无量纲化
# 熵值法-正向指标处理 def normalize_entropy_positive(data, train_split): data_max = data[:train_split].max(axis=0) data_min = data[:train_split].min(axis=0) return (data - data_min) / (data_max-data_min) # data:数据 # train_split训练集索引 # 熵值法-负向指标处理 def normalize_entropy_negative(data, train_split): data_max = data[:train_split].max(axis=0) data_min = data[:train_split].min(axis=0) return (data_max - data) / (data_max-data_min) # 熵值法-中性指标处理 def normalize_entropy_middle(data, train_split): data_mean = data[:train_split].mean(axis=0) data_max = data[:train_split].max(axis=0) data_min = data[:train_split].min(axis=0) new_data = data.copy() new_data[data<data_mean] = (data - data_min) / (data_mean-data_min) new_data[data>=data_mean] = (data_max - data) / (data_max-data_mean) return new_data
df = df_src.copy() df[l_target_positive] = normalize_entropy_positive(df[l_target_positive],len(df)) df[l_target_negative] = normalize_entropy_negative(df[l_target_negative],len(df)) df[l_target_middle] = normalize_entropy_middle(df[l_target_middle],len(df))
4.3 非负平移
df = df + 1
4.4 求各指标在各方案下的比值
# 熵值法-计算比重 def normalize_entropy_calculate_frequency(data, train_split): data_sum = data[:train_split].sum(axis=0) return data / data_sum df = normalize_entropy_calculate_frequency(df,len(df))
4.5 求各指标信息熵、效用、权重
# 计算指标熵值,效用,权重 def cal_entropy(x): m = len(x) r1 = -1/np.log(m) * np.sum(x * x.map(np.log)) r2 = 1-r1 return (r1,r2) df_entropy = df.apply(cal_entropy, axis=0,result_type='expand').T df_entropy.columns = ['信息熵','效用值'] df_entropy['权重'] = df_entropy['效用值']/np.sum(df_entropy['效用值'])
4.6 计算综合指标权重
层级关系如下,相加得出权重。
l_target_economy = ['x1','x2','x3','x4'] # r1指标 l_target_finance = ['x5','x6','x7'] # r2指标 l_target_self = ['x8','x9','x10','x11','x12','x13','x14','x15'] # r3指标
# 计算综合指标权重 df_out2 = df_entropy['权重'].to_frame().T df_out2['r1'] = df_out2[l_target_economy].sum(axis=1) df_out2['r2'] = df_out2[l_target_finance].sum(axis=1) df_out2['r3'] = df_out2[l_target_self].sum(axis=1)
4.7 计算综合得分
# 计算分指标综合得分 df_out = df * df_entropy['权重'].T df_out['r1'] = df_out[l_target_economy].sum(axis=1) df_out['r2'] = df_out[l_target_finance].sum(axis=1) df_out['r3'] = df_out[l_target_self].sum(axis=1) df_out['r4'] = df_out[l_target_economy+l_target_finance+l_target_self].sum(axis=1)
小结
各类赋权方法的科学性,统计学届还在探讨,居中的方法就是,使用主观赋权和客观赋权相互应征。




