Nowcoder OI赛制测试2 F 假的数学题 - 斯特林公式 + 二分

Description

给定$X$， 找到最小的$N$ 使得$N! > X^X$

数据范围：  $x <= 1e11$

Solution

$X^X$ 太大， 高精也存不过， 所以取对数 : $lg(X^X)$ = Xlg(X)，即要求出最小$N$的使得$lg(N!) > Xlg(X)$

N!有单调性， 可以使用二分答案来求出N， 但是每次$check$的复杂度是$O(N)$， 我们必须要进行优化。

通过斯特林公式 : 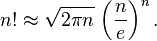      ， 取对数后:  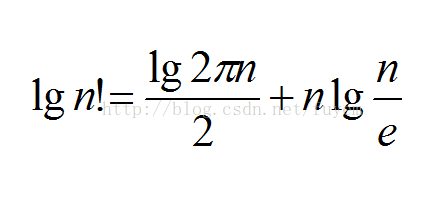  (图片都是转发的QuQ）

就可以在$O(1)$时间内算出$lg(N!)$ 并check。 总复杂度$O(logN)$

Code

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define lb long double
#define ll long long
#define e 2.7182818284590453254
using namespace std;

lb n, x;

bool check(ll o) {
    lb pi = acos(-1);
    n = o;
    n = log(2 * pi * n) / 2 + n * log(n / e);
    if(n > x) return 1;
    else return 0;
}

int main()
{
    scanf("%llf", &x);
    x = x * log(x);
    ll l = 0, r = 1e18, ans = 0;
    while(l <= r) {
        ll mid = (l + r) >> 1;
        if(check(mid)) ans = mid, r = mid - 1;
        else l = mid + 1;
    }
    printf("%lld\n", ans);
}