noip2010 引水入城 - bfs + 贪心

题目描述

在一个遥远的国度，一侧是风景秀美的湖泊，另一侧则是漫无边际的沙漠。该国的行政区划十分特殊，刚好构成一个 NN 行 \times M×M 列的矩形，如上图所示，其中每个格子都代表一座城市，每座城市都有一个海拔高度。

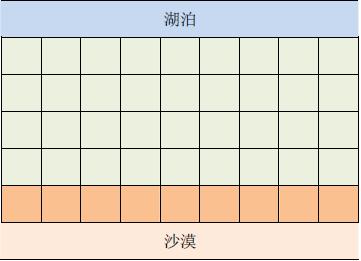
为了使居民们都尽可能饮用到清澈的湖水，现在要在某些城市建造水利设施。水利设施有两种，分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。

因此，只有与湖泊毗邻的第 11 行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差，将湖水从高处向低处输送。故一座城市能建造输水站的前提，是存在比它海拔更高且拥有公共边的相邻城市，已经建有水利设施。由于第 NN 行的城市靠近沙漠，是该国的干旱区，所以要求其中的每座城市都建有水利设施。那么，这个要求能否满足呢？如果能，请计算最少建造几个蓄水厂；如果不能，求干旱区中不可能建有水利设施的城市数目。

输入输出格式

输入格式：

 

每行两个数，之间用一个空格隔开。输入的第一行是两个正整数 N,MN,M ，表示矩形的规模。接下来 NN 行，每行 MM 个正整数，依次代表每座城市的海拔高度。

 

输出格式：

 

两行。如果能满足要求，输出的第一行是整数 11 ，第二行是一个整数，代表最少建造几个蓄水厂；如果不能满足要求，输出的第一行是整数 00 ，第二行是一个整数，代表有几座干旱区中的城市不可能建有水利设施。

 

 

题解

先对于每一个沿湖城市做一遍bfs， 求出从那个城市出发能够到达的沙漠旁的城市的区间， 若不是一段区间， 则必定不能全部覆盖， 做完bfs后可以直接判断。

接着再贪心区间覆盖， 求出最少的区间数， 即为答案

 

 

 

代码

#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#define rd read()
#define rep(i,a,b) for( int i = (a); i <= (b); ++i )
#define per(i,a,b) for( int i = (a); i >= (b); --i )
using namespace std;
typedef pair<int, int> P;

queue<P>q;

const int N = 505, inf = 1061109567;

int n, m, h[N][N], vis[N][N], ok[N], tot ;

int dx[4] = {0, 0, -1, 1}, dy[4] = {1, -1, 0, 0};

struct node {
    int l, r;
}ln[N];

int read() {
    int X = 0, p = 1; char c = getchar();
    for(; c > '9' || c < '0'; c = getchar() ) if( c == '-' ) p = -1;
    for(; c >= '0' && c <= '9'; c = getchar() ) X = X * 10 + c - '0';
    return X * p;
}

void bfs( int x ) {
    memset(vis, 0, sizeof(vis));
    q.push( P( 1, x ) );
    vis[1][x] = 1;
    ln[x].l = n + 1, ln[x].r = 0;
    if( n == 1 && !ok[x] ) {
        ok[x] = 1;
        tot++;
        ln[x].l = x;
        ln[x].r = x;
    }
    for( P u, to; !q.empty(); ) {
        u = q.front(); q.pop();
        for( int i = 0; i < 4; ++i ) {
            int nx = u.first + dx[i], ny = u.second + dy[i];
            if( !nx || !ny || nx > n || ny > m || vis[nx][ny]) continue;
            if( h[nx][ny] >= h[u.first][u.second] ) continue;
            vis[nx][ny] = 1;
            if( nx == n ) {
                ln[x].l = min( ln[x].l, ny);
                ln[x].r = max( ln[x].r, ny);
                if( !ok[ny] ) ok[ny] = 1, tot++;
            }
            q.push( P( nx, ny ) );
        }
    }
}

int cmp( const node &A, const node &B ) {
    return A.l == B.l ? A.r < B.r : A.l < B.l;
}

int main()
{
    n = rd, m = rd;
    rep( i, 1, n ) rep( j, 1, m ) h[i][j] = rd;
    rep( i, 1, m ) if( h[1][i] >= h[1][i - 1] && h[1][i] >= h[1][i + 1]) bfs( i );
    if( tot != m ) return printf("0\n%d\n", m - tot), 0;
    sort(ln + 1, ln + 1 + m, cmp);
    int l = 1, r = 1, ans = 0, now = 1;
    for(; r <= m; ) {
        for(; ln[now].l <= r && now <= m; now++ )    l = max( l, ln[now].r );
        ans++;
        r = l + 1;
    }
    printf("1\n%d\n", ans);
}