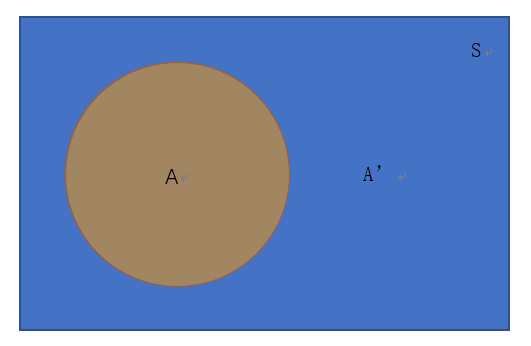
假设有事件A和事件B，可以同时发生但不是完全同时发生，如以下韦恩图所示：
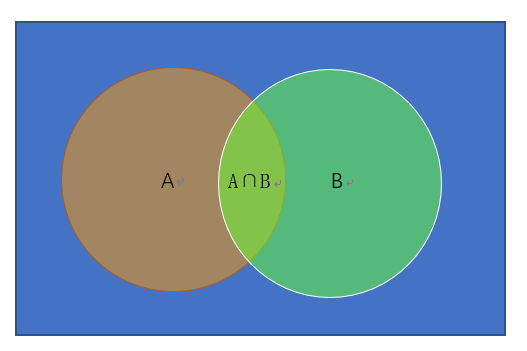
其中，A∩B表示A和B的并集，即A和B同时发生的概率。
如此，我们很容易得出，在事件B发生的情况下，事件A发生的概率为：
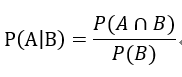
这个P(A|B)就是条件概率(Conditional Probability)。
同理，在事件A发生的情况下，事件B发生的概率为：
由以上式子可得：
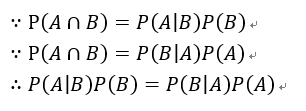
再调整一下，变成：
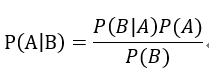
这个就是著名的贝叶斯公式的基本形态了，其中：
P(A|B)叫做后验概率(Posterior Probability)
P(A)叫做先验概率(Prior Probability)
P(B|A)/P(B)叫做似然度(Likelihood)
那么我们可以看出，贝叶斯定理可以比较简单的归纳为：
后验概率=先验概率*似然度
在日常使用中，如贝叶斯分类、贝叶斯回归、贝叶斯滤波等算法，普遍使用迭代和归一化的方法来计算似然度，为了更好的了解归一化的方法，这里还有一个基础概念，叫全概率公式。
接着之前的说法，很明显有
OK，先举几个经典的例子来帮助理解：
一座别墅在过去的 20 年里一共发生过 2 次被盗，别墅的主人有一条狗，狗平均每周晚上叫 3 次，假设在盗贼入侵时狗叫的概率被估计为 0.9，问题是：在狗叫的时候发生入侵的概率是多少？
我们假设：
事件A：狗在晚上叫
事件B：盗贼入侵
以天为单位统计,有：
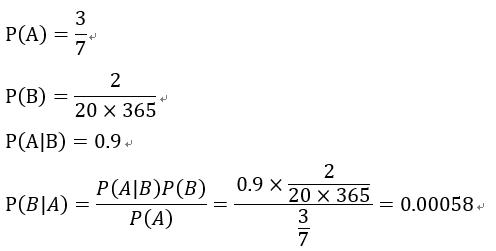
可以看到，最终的结果基本是不可能。
这只是一个最简单的例子，其中，别墅在过去的20年中被盗2次、狗平均每周晚上叫3次这些都是先验统计，而在现实应用中往往是根据上一步的事件去推断下一步的事件，这个迭代的过程往往是很多算法实现的基础。
下面，我们举一个更复杂一些的例子：
假设有两个各装了100个球的箱子，A箱子中有70个红球，30个蓝球，B箱子中有30个红球，70个蓝球。假设随机选择其中一个箱子，从中拿出一个球记下球色再放回原箱子，如此重复12次，记录得到8次红球，4次蓝球。问题来了，你认为被选择的箱子是A箱子的概率有多大？
我们假设得到小球的结果顺序如下：红红红红红红红红蓝蓝蓝蓝，用C++实现：
#include <iostream> #include <cmath> #include <iomanip> #include <vector> #include <cstdlib> #include <ctime> #include <limits> class balls_case_problem { private: double p_a; double p_b; double p_red_in_a; double p_blue_in_a; double p_red_in_b; double p_blue_in_b; public: balls_case_problem(int red_balls_in_a, int blue_balls_in_a, int red_balls_in_b, int blue_balls_in_b) { p_a = 0.5; p_b = 1 - p_a; p_red_in_a = (double)red_balls_in_a / (double)(red_balls_in_a + blue_balls_in_a); p_blue_in_a = 1 - p_red_in_a; p_red_in_b = (double)red_balls_in_b / (double)(red_balls_in_b + blue_balls_in_b); p_blue_in_b = 1 - p_red_in_b; } ~balls_case_problem(){}; void got_red() { p_a = (p_red_in_a * p_a) / ((p_red_in_a * p_a) + (p_red_in_b * p_b)); p_b = 1 - p_a; } void got_blue() { p_a = (p_blue_in_a * p_a) / ((p_blue_in_a * p_a) + (p_blue_in_b * p_b)); p_b = 1 - p_a; } double get_p_a() { return p_a; } double get_p_b() { return p_b; } }; int main() { int red_ball_results[] = {1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0}; balls_case_problem problem(70, 30, 30, 70); for(int i = 0; i < sizeof(red_ball_results) / sizeof(int); i++) { if(red_ball_results[i] == 1) { problem.got_red(); }else{ problem.got_blue(); } std::cout << "Probility of chose case A: " << problem.get_p_a() << std::endl; } return 0; }
运行结果为：
Probility of chose case A: 0.7 Probility of chose case A: 0.844828 Probility of chose case A: 0.927027 Probility of chose case A: 0.967365 Probility of chose case A: 0.985748 Probility of chose case A: 0.993842 Probility of chose case A: 0.997351 Probility of chose case A: 0.998863 Probility of chose case A: 0.997351 Probility of chose case A: 0.993842 Probility of chose case A: 0.985748 Probility of chose case A: 0.967365
