[算法总结]并查集
目录
一、关于并查集
1. 定义
并查集(Disjoint-Set)是一种可以动态维护若干个不重叠的集合，并支持合并与查询两种操作的一种数据结构。
2. 基本操作
1. 合并(Union/Merge)[1]：合并两个集合。
2. 查询(Find/Get)：查询元素所属集合。
实际操作时，我们会使用一个点来代表整个集合，即一个元素的根结点(可以理解为父亲)。
3. 具体实现
我们建立一个数组fa[ ]或pre[ ]表示一个并查集，fa[i]表示i的父节点。
初始化：每一个点都是一个集合，因此自己的父节点就是自己fa[i]=i
查询：每一个节点不断寻找自己的父节点，若此时自己的父节点就是自己，那么该点为集合的根结点，返回该点。
修改：合并两个集合只需要合并两个集合的根结点，即fa[RootA]=RootB，其中RootA,RootB是两个元素的根结点。
路径压缩：
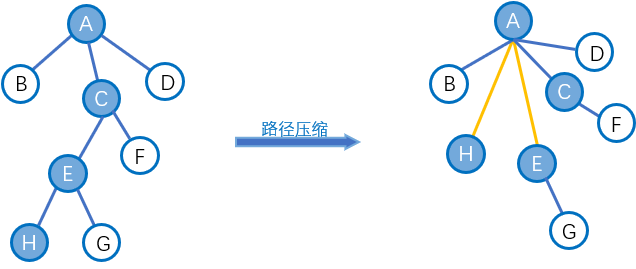
实际上，我们在查询过程中只关心根结点是什么，并不关心这棵树的形态(有一些题除外)。因此我们可以在查询操作的时候将访问过的每个点都指向树根，这样的方法叫做路径压缩，单次操作复杂度为\(O(logN)\)。
结合下图食用更好(图为状态压缩的过程)：
二、代码实现
初始化的模板：
for(int i=1;i<=n;i++) pre[i]=i;
查询的模板(含路径压缩)：
int Find(int x){
if(x==pre[x]) return x;
return pre[x]=Find(pre[x]);
}
合并的模板：
void merge(int x,int y){
int fx=Find(x),fy=Find(y);
if(fx!=fy) pre[fx]=fy;
}
//主函数内
merge(a,b);
三、一些例题
例1：P1551 亲戚
模板题。这里就不放代码了...
同样是模板题：P2814 家谱，建议使用map(STL)。
例2：P1536 村村通
求出让所有道路联通时要建多少条道路。
我们先把已经建好的道路的点合并，如果还需要建道路，那么所有点组成的集合数量一定大于1。
我们只要查询是否单个点组成了一个集合，即询问一个点的父节点是否为本身。
值得注意的是最终合并为一个集合中的根结点的父节点也是其本身，我们最后输出答案的时候要减掉。
Code：
#include <bits/stdc++.h>
using namespace std;
int pre[1000001],n,m,ans;
inline int Find(int x){
return pre[x]==x?x:pre[x]=Find(pre[x]);
}
inline void Union(int x, int y){
int fx=Find(x),fy=Find(y);
if(fx!=fy) pre[fx]=fy;
}
int main()
{
while(scanf("%d",&n)&&n){
ans=0;
scanf("%d", &m);
for(int i=1;i<=n;i++) pre[i]=i;
for(int i=1,x,y;i<=m;i++){
scanf("%d%d",&x,&y);
Union(x,y);
}
for(int i=1;i<=n;i++){
if(Find(i)==i) ans++;
}
printf("%d\n",ans-1);
}
return 0;
}
例3：P1396 营救
FBI！Open UP！看到求最大值的最小我们知道一定会用二分解决。
顺着这个思路走，我们可以二分这个拥挤度，在判断这个拥挤度是否可行时，把所有拥挤度大于mid的边都去掉，最后并查集判断s点与t点是否联通即可。
Code：
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define N 50050
using namespace std;
int l=INF,r=-1,n,m,s,t,ans;
int pre[N],x[N],y[N],cost[N];
inline int find(int x){return x==pre[x]?x:pre[x]=find(pre[x]);}
inline int check(int mid){
for(int i=1;i<=n;i++) pre[i]=i;
for(int i=1;i<=m;i++){
if(cost[i]>mid) continue;
int fx=find(x[i]),fy=find(y[i]);
if(fx!=fy) pre[fx]=fy;
}
if(find(s)==find(t)) return 1;
return 0;
}
int main()
{
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&x[i],&y[i],&cost[i]);
l=min(l,cost[i]);r=max(r,cost[i]);
}
while(l<=r){
int mid=(l+r)>>1;
if(check(mid)){
r=mid-1;
ans=mid;
}
else l=mid+1;
}
printf("%d",ans);
return 0;
}
例4：P1621 集合
把所有质因数大于p的数都求出来合并，最后并查集求解。
#include<bits/stdc++.h>
#define N 100010
using namespace std;
int a,b,cmp,ans,cnt;
int pre[N],notp[N],p[N];
int Find(int x){
if(x==pre[x]) return x;
return pre[x]=Find(pre[x]);
}
inline int Union(int x,int y){
int fx=Find(x),fy=Find(y);
if(fx!=fy) pre[fx]=fy;
}
inline void E_prime(){
notp[1]=1;
for(int i=2;i<=b;i++){
if(notp[i]) continue;
for(int j=i*2;j<=b;j+=i){
notp[j]=1;
}
}
for(int i=cmp;i<=b;i++)
if(not notp[i]) p[++cnt]=i;
}
int main()
{
scanf("%d%d%d",&a,&b,&cmp);
for(int i=a;i<=b;i++) pre[i]=i;
E_prime();
for(int i=1;i<=cnt;i++)
for(int j=2;j*p[i]<=b;j++)
if(j*p[i]>=a&&(j-1)*p[i]>=a)
Union(p[i]*j,p[i]*(j-1));
for(int i=a;i<=b;i++)
if(pre[i]==i) ans++;
printf("%d",ans);
return 0;
}
例5：P4185 [USACO18JAN]MooTube
把K和边权从大往小排序，这样大的K也满足小的K，避免了重复搜索。
Code：
#include<bits/stdc++.h>
#define N 300010
using namespace std;
int n,q,fa[N],size[N],ans[N];
inline int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
inline void Union(int x,int y){
int fx=find(x),fy=find(y);
if(fx==fy) return;
size[fx]+=size[fy],fa[fy]=fx;
}
struct edge{
int u,v,r;
}p[N];
struct node{
int k,v,id;
}ask[N];
inline int CMP(edge a,edge b){return a.r>b.r;}
inline int cmp(node a,node b){return a.k>b.k;}
int main()
{
scanf("%d%d",&n,&q);
for(int i=1;i<n;i++)
scanf("%d%d%d",&p[i].u,&p[i].v,&p[i].r);
for(int i=1;i<=q;i++)
scanf("%d%d",&ask[i].k,&ask[i].v),ask[i].id=i;
for(int i=1;i<=n;i++){fa[i]=i;size[i]=1;}
sort(p+1,p+n,CMP);
sort(ask+1,ask+q+1,cmp);
int pos=1;
for(int i=1;i<=q;i++){
while(pos<n&&p[pos].r>=ask[i].k){
Union(p[pos].u,p[pos].v);
pos++;
}
ans[ask[i].id]=size[find(ask[i].v)]-1;
}
for(int i=1;i<=q;i++)
printf("%d\n",ans[i]);
return 0;
}
例6：P1197 [JSOI2008]星球大战
题目要求求出每次打击后图中连通块的个数。并查集可以进行合并操作，却不能进行分离操作，所以我们倒序处理。先联通没有被炸的点并统计出此时连通块的个数，接着不断合并被炸的点并统计此时的连通块个数。
Code：
#include<bits/stdc++.h>
#define N 400010
using namespace std;
int n,m,k,pre[N],first[N],nxt[N],go[N];
int poi[N],off[N],tot,from[N],sum,ans[N];
inline void add_edge(int u,int v){
nxt[++tot]=first[u];
first[u]=tot;
go[tot]=v;
from[tot]=u;
}
inline int Find(int x){
return x==pre[x]?x:pre[x]=Find(pre[x]);
}
inline void Union(int x,int y){
int fx=Find(x),fy=Find(y);
if(fx!=fy) pre[fx]=fy;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) pre[i]=i;
for(int i=1,x,y;i<=m;i++){
scanf("%d%d",&x,&y);
add_edge(x,y);
add_edge(y,x);
}
scanf("%d",&k);
for(int i=1;i<=k;i++){
scanf("%d",&poi[i]);
off[poi[i]]=1;//标记
}
sum=n-k;//剩余的点
for(int i=1;i<=m<<1;i++)//双向边
if(!off[from[i]]&&!off[go[i]])//两个点都没被炸
if(Find(from[i])!=Find(go[i]))
sum--,Union(from[i],go[i]);//合并，更新连通块个数
ans[k+1]=sum;//最后一个答案
for(int i=k;i>=1;i--){
sum++;//恢复这个点后自己也算一个连通块，因此个数要+1
off[poi[i]]=0;//恢复
for(int e=first[poi[i]];e;e=nxt[e]){
int v=go[e];
if(!off[v]&&Find(poi[i])!=Find(v)){
Union(poi[i],v);//合并
sum--;
}
}
ans[i]=sum;
}
for(int i=1;i<=k+1;i++)
printf("%d\n",ans[i]);
return 0;
}
例7：bzoj2054疯狂的馒头
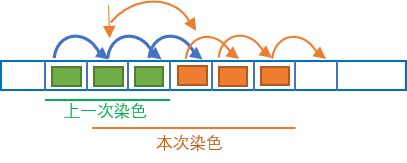
我们发现最后满头染上的颜色只与他最后一次被染上的颜色有关，因此我们倒着处理，这时我们需要维护已经染好的馒头不会再被染色。从区间的左向右依次扫描，寻找这个点的父亲，此时这个父亲就是还没有被填上颜色的节点(如果这个父亲节点仍在区间里)，我们把这个点染色并标记这个点指向下一个节点。简明的来讲，就是当我们想对一个点染色时，这个点会把我们带到另一个没有染色的点来染色。
#include<bits/stdc++.h>//每次扫描的元素被染色后指向其没有被染色的馒头
#define N 1000010 //路径压缩以节省时间
#define ll long long
using namespace std;
int n,m,p,q;
int pre[N],ans[N];
inline int Find(int x){
return (pre[x]==x)? x:pre[x]=Find(pre[x]);
}
inline void Dye_mantou(ll l,ll r,int color)
{
for(int i=Find(l);i<=r;i=Find(i)){ //方向指向数组末尾
ans[i]=color;
pre[i]=i+1;
}
}
int main()
{
scanf("%d%d%d%d",&n,&m,&p,&q);
for(int i=1;i<=n+1;i++) pre[i]=i;
for(int i=m;i>=1;i--){
ll l=(i*p+q)%n+1;
ll r=(i*q+p)%n+1;
if(l>r) swap(l,r);
Dye_mantou(l,r,i);
}
for(int i=1;i<=n;i++)
printf("%d\n",ans[i]);
return 0;
}
例8：P2294 [HNOI2005]狡猾的商人
带权并查集。通过并查集建立月份与月份的关系。
Code：
#include<bits/stdc++.h>
#define N 100010
using namespace std;
int n,m,w;
int pre[N],d[N];
int Find(int x){
if(pre[x]==x) return x;
int temp=Find(pre[x]);
d[x]+=d[pre[x]];
return pre[x]=temp;
}
int Union(int x,int y,int v)
{
int fx=Find(x);
int fy=Find(y);
if(fx==fy)
return d[x]-d[y]==v;
if(fx<fy){
pre[fx]=fy;
d[fx]=d[y]+v-d[x];
return 1;
}
else{
pre[fy]=fx;
d[fy]=d[x]-v-d[y];
return 1;
}
}
int main()
{
scanf("%d",&w);
while(w--)
{
scanf("%d%d",&n,&m);
int flag=1;
memset(d,0,sizeof(d));
for(int i=0;i<=n;i++) pre[i]=i;
for(int i=1,s,t,v;i<=m;i++){
scanf("%d%d%d",&s,&t,&v);
if(flag==0) continue;
if(!Union(s-1,t,v)) flag=0;//包含s月，所以往前一个月为s-1
}
if(flag) printf("true\n");
else printf("false\n");
}
return 0;
}
例9：P1892 [BOI2003]团伙
题目的两种关系已经说得很明确了，我们将朋友关系的两个人合并。对于是敌人关系的两个人，由于敌人的敌人是我的朋友，所以我们可以建立一个自己虚拟的敌人再与对方形成朋友关系。
Code：
#include<bits/stdc++.h>
#define N 6000
using namespace std;
int n,m,ans,pre[N];
char ch;
int Find(int x){
return (x==pre[x])? x:pre[x]=Find(pre[x]);
}
inline void Union(int x,int y){
int fx=Find(x);
int fy=Find(y);
pre[fx]=fy;
return;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=2*n;i++) pre[i]=i;
for(int i=1,u,v;i<=m;i++){
cin>>ch>>u>>v;
if(ch=='F') Union(u,v);
if(ch=='E'){
pre[Find(u+n)]=Find(v);
pre[Find(v+n)]=Find(u);
}
}
for(int i=1;i<=n;i++)
if(pre[i]==i) ans++;
printf("%d",ans);
return 0;
}
怎么起名都无所谓啦 ↩︎
