《数据挖掘：理论与算法》学习笔记（五）—决策树

决策树模型

决策树是一种用于对实例进行分类的树形结构。决策树由节点（node）和有向边（directed edge）组成。节点的类型有两种：内部节点和叶子节点。其中，内部节点表示一个特征或属性的测试条件（用于分开具有不同特性的记录），叶子节点表示一个分类。

一旦我们构造了一个决策树模型，以它为基础来进行分类将是非常容易的。具体做法是，从根节点开始，地实例的某一特征进行测试，根据测试结构将实例分配到其子节点；沿着该分支可能达到叶子节点或者到达另一个内部节点时，那么就使用新的测试条件递归执行下去，直到抵达一个叶子节点。当到达叶子节点时，我们便得到了最终的分类结果。

对于决策树算法，我们需要注意以下几点：

• 对于同一个数据集，我们可以构造出不同的决策树
• 较为简单的决策树通常效果更好
• 一般推荐区分度强的在第一个数根，叶节点作为补充。

决策树算法

ID3算法
ID3算法是决策树的一种，它是基于奥卡姆剃刀原理的，即用尽量用较少的东西做更多的事。越是小型的决策树越优于大的决策树。

在信息论中，期望信息越小，那么信息增益就越大，从而纯度就越高。ID3算法的核心思想就是以信息增益来度量属性的选择，选择分裂后信息增益最大的属性进行分裂。该算法采用自顶向下的贪婪搜索遍历可能的决策空间。

熵：“熵”就是关于不确定性的一个极好的数学描述
熵的计算公式如下：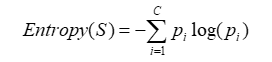

例子：

在上面的例子中，事件S的不确定性达到了0.940
加入属性A的判断后，事件S的不确定性会下降，而 Gain(S,A) 我们称之为信息增益。也就是加入属性A的判断，会把事件S的不确定性降低的程度。

例如，在上图中，加入District 属性带来的信息增益为 0.247 ，而加入 Income 属性带来的信息增益为 0.152 ，所以我们更偏向于选择District 属性。

ID3算法的核心问题是选取在树的每个节点要测试的属性

ID3算法框架
建树—递归结构

例子如下

防止过拟合的方法
1、提前停止树的生长
2、进行剪枝

其中第一种方法更直观，但精确地估计何时停止树增长很困难
第二种方法被证明在实践中更成功

熵的偏差
下面是一个惩罚公式，分子是 Gain(S,A)，而分母是分裂的特征个数，作为一种有效的惩罚措施。
比如，单纯的按生日辨别男女，Gain(S,A) 很大，entrpy为0，但是这给系统一个错误的细化特征的倾向，实际上，每个人一条规则肯定是不合适的。

 

参考文献：清华大学-数据挖掘：理论与算法（国家级精品课）